Quanquan Gu
Group Representational Position Encoding
Dec 08, 2025Abstract:We present GRAPE (Group RepresentAtional Position Encoding), a unified framework for positional encoding based on group actions. GRAPE brings together two families of mechanisms: (i) multiplicative rotations (Multiplicative GRAPE) in $\mathrm{SO}(d)$ and (ii) additive logit biases (Additive GRAPE) arising from unipotent actions in the general linear group $\mathrm{GL}$. In Multiplicative GRAPE, a position $n \in \mathbb{Z}$ (or $t \in \mathbb{R}$) acts as $\mathbf{G}(n)=\exp(n\,ω\,\mathbf{L})$ with a rank-2 skew generator $\mathbf{L} \in \mathbb{R}^{d \times d}$, yielding a relative, compositional, norm-preserving map with a closed-form matrix exponential. RoPE is recovered exactly when the $d/2$ planes are the canonical coordinate pairs with log-uniform spectrum. Learned commuting subspaces and compact non-commuting mixtures strictly extend this geometry to capture cross-subspace feature coupling at $O(d)$ and $O(r d)$ cost per head, respectively. In Additive GRAPE, additive logits arise as rank-1 (or low-rank) unipotent actions, recovering ALiBi and the Forgetting Transformer (FoX) as exact special cases while preserving an exact relative law and streaming cacheability. Altogether, GRAPE supplies a principled design space for positional geometry in long-context models, subsuming RoPE and ALiBi as special cases. Project Page: https://github.com/model-architectures/GRAPE.
Higher-order Linear Attention
Oct 31, 2025Abstract:The quadratic cost of scaled dot-product attention is a central obstacle to scaling autoregressive language models to long contexts. Linear-time attention and State Space Models (SSMs) provide scalable alternatives but are typically restricted to first-order or kernel-based approximations, which can limit expressivity. We introduce Higher-order Linear Attention (HLA), a causal, streaming mechanism that realizes higher interactions via compact prefix sufficient statistics. In the second-order case, HLA maintains a constant-size state and computes per-token outputs in linear time without materializing any $n \times n$ matrices. We give closed-form streaming identities, a strictly causal masked variant using two additional summaries, and a chunk-parallel training scheme based on associative scans that reproduces the activations of a serial recurrence exactly. We further outline extensions to third and higher orders. Collectively, these results position HLA as a principled, scalable building block that combines attention-like, data-dependent mixing with the efficiency of modern recurrent architectures. Project Page: https://github.com/yifanzhang-pro/HLA.
Causal Attention with Lookahead Keys
Sep 09, 2025Abstract:In standard causal attention, each token's query, key, and value (QKV) are static and encode only preceding context. We introduce CAuSal aTtention with Lookahead kEys (CASTLE), an attention mechanism that continually updates each token's keys as the context unfolds. We term these updated keys lookahead keys because they belong to earlier positions yet integrate information from tokens that appear later relative to those positions, while strictly preserving the autoregressive property. Although the mechanism appears sequential, we derive a mathematical equivalence that avoids explicitly materializing lookahead keys at each position and enables efficient parallel training. On language modeling benchmarks, CASTLE consistently outperforms standard causal attention across model scales, reducing validation perplexity and improving performance on a range of downstream tasks.
SwingArena: Competitive Programming Arena for Long-context GitHub Issue Solving
May 29, 2025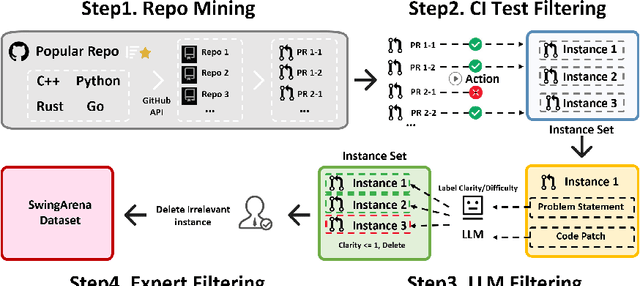
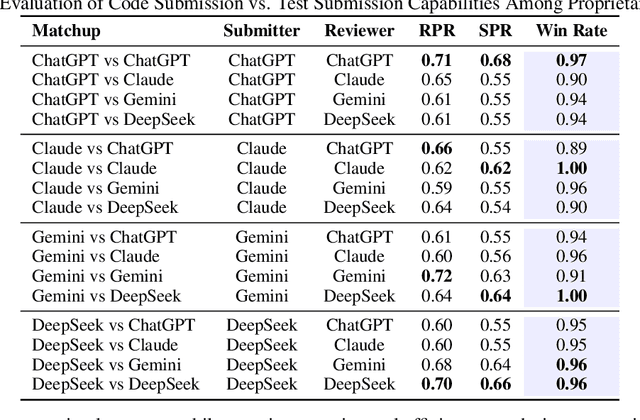
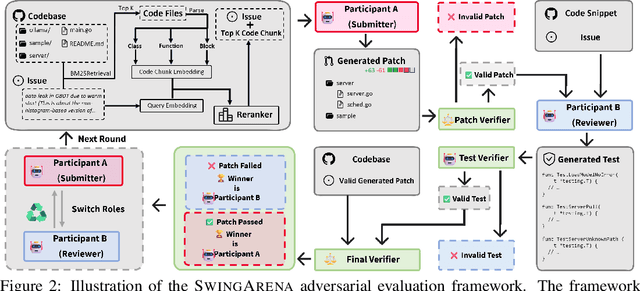
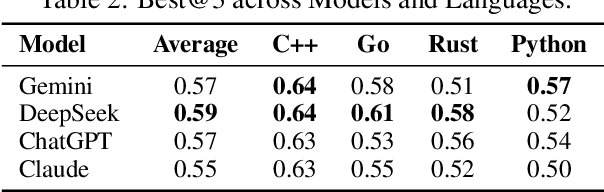
Abstract:We present SwingArena, a competitive evaluation framework for Large Language Models (LLMs) that closely mirrors real-world software development workflows. Unlike traditional static benchmarks, SwingArena models the collaborative process of software iteration by pairing LLMs as submitters, who generate patches, and reviewers, who create test cases and verify the patches through continuous integration (CI) pipelines. To support these interactive evaluations, we introduce a retrieval-augmented code generation (RACG) module that efficiently handles long-context challenges by providing syntactically and semantically relevant code snippets from large codebases, supporting multiple programming languages (C++, Python, Rust, and Go). This enables the framework to scale across diverse tasks and contexts while respecting token limitations. Our experiments, using over 400 high-quality real-world GitHub issues selected from a pool of 2,300 issues, show that models like GPT-4o excel at aggressive patch generation, whereas DeepSeek and Gemini prioritize correctness in CI validation. SwingArena presents a scalable and extensible methodology for evaluating LLMs in realistic, CI-driven software development settings. More details are available on our project page: swing-bench.github.io
Designing Cyclic Peptides via Harmonic SDE with Atom-Bond Modeling
May 27, 2025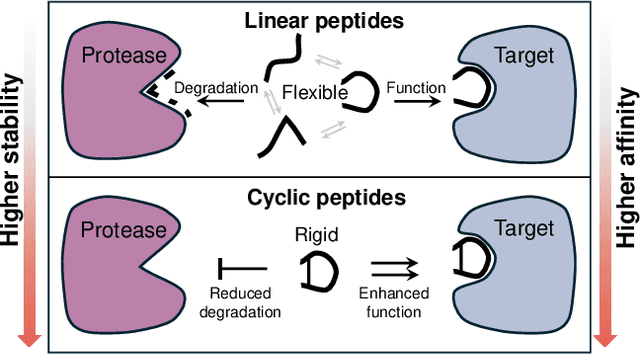
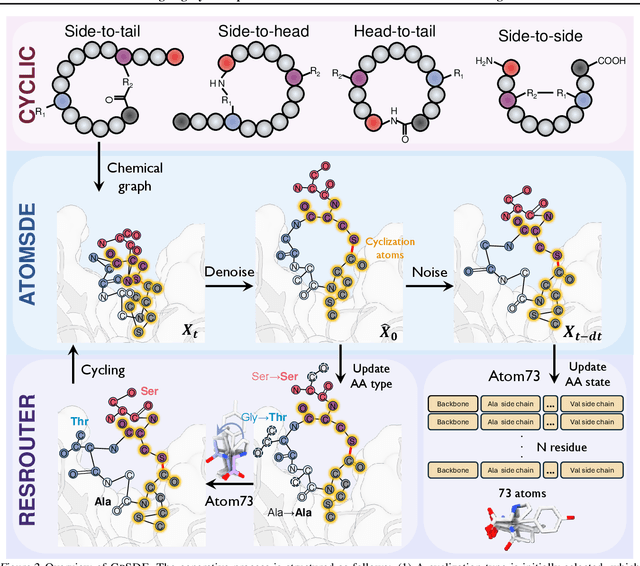
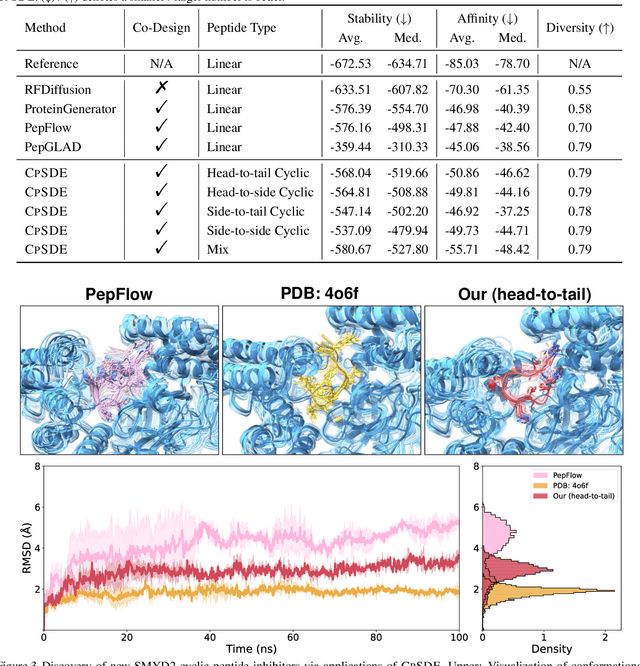
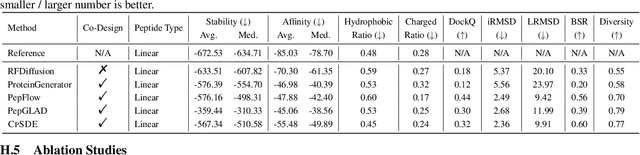
Abstract:Cyclic peptides offer inherent advantages in pharmaceuticals. For example, cyclic peptides are more resistant to enzymatic hydrolysis compared to linear peptides and usually exhibit excellent stability and affinity. Although deep generative models have achieved great success in linear peptide design, several challenges prevent the development of computational methods for designing diverse types of cyclic peptides. These challenges include the scarcity of 3D structural data on target proteins and associated cyclic peptide ligands, the geometric constraints that cyclization imposes, and the involvement of non-canonical amino acids in cyclization. To address the above challenges, we introduce CpSDE, which consists of two key components: AtomSDE, a generative structure prediction model based on harmonic SDE, and ResRouter, a residue type predictor. Utilizing a routed sampling algorithm that alternates between these two models to iteratively update sequences and structures, CpSDE facilitates the generation of cyclic peptides. By employing explicit all-atom and bond modeling, CpSDE overcomes existing data limitations and is proficient in designing a wide variety of cyclic peptides. Our experimental results demonstrate that the cyclic peptides designed by our method exhibit reliable stability and affinity.
Simultaneous Modeling of Protein Conformation and Dynamics via Autoregression
May 23, 2025Abstract:Understanding protein dynamics is critical for elucidating their biological functions. The increasing availability of molecular dynamics (MD) data enables the training of deep generative models to efficiently explore the conformational space of proteins. However, existing approaches either fail to explicitly capture the temporal dependencies between conformations or do not support direct generation of time-independent samples. To address these limitations, we introduce ConfRover, an autoregressive model that simultaneously learns protein conformation and dynamics from MD trajectories, supporting both time-dependent and time-independent sampling. At the core of our model is a modular architecture comprising: (i) an encoding layer, adapted from protein folding models, that embeds protein-specific information and conformation at each time frame into a latent space; (ii) a temporal module, a sequence model that captures conformational dynamics across frames; and (iii) an SE(3) diffusion model as the structure decoder, generating conformations in continuous space. Experiments on ATLAS, a large-scale protein MD dataset of diverse structures, demonstrate the effectiveness of our model in learning conformational dynamics and supporting a wide range of downstream tasks. ConfRover is the first model to sample both protein conformations and trajectories within a single framework, offering a novel and flexible approach for learning from protein MD data.
On the Design of KL-Regularized Policy Gradient Algorithms for LLM Reasoning
May 23, 2025Abstract:Policy gradient algorithms have been successfully applied to enhance the reasoning capabilities of large language models (LLMs). Despite the widespread use of Kullback-Leibler (KL) regularization in policy gradient algorithms to stabilize training, the systematic exploration of how different KL divergence formulations can be estimated and integrated into surrogate loss functions for online reinforcement learning (RL) presents a nuanced and systematically explorable design space. In this paper, we propose regularized policy gradient (RPG), a systematic framework for deriving and analyzing KL-regularized policy gradient methods in the online RL setting. We derive policy gradients and corresponding surrogate loss functions for objectives regularized by both forward and reverse KL divergences, considering both normalized and unnormalized policy distributions. Furthermore, we present derivations for fully differentiable loss functions as well as REINFORCE-style gradient estimators, accommodating diverse algorithmic needs. We conduct extensive experiments on RL for LLM reasoning using these methods, showing improved or competitive results in terms of training stability and performance compared to strong baselines such as GRPO, REINFORCE++, and DAPO. The code is available at https://github.com/complex-reasoning/RPG.
An All-Atom Generative Model for Designing Protein Complexes
Apr 17, 2025Abstract:Proteins typically exist in complexes, interacting with other proteins or biomolecules to perform their specific biological roles. Research on single-chain protein modeling has been extensively and deeply explored, with advancements seen in models like the series of ESM and AlphaFold. Despite these developments, the study and modeling of multi-chain proteins remain largely uncharted, though they are vital for understanding biological functions. Recognizing the importance of these interactions, we introduce APM (All-Atom Protein Generative Model), a model specifically designed for modeling multi-chain proteins. By integrating atom-level information and leveraging data on multi-chain proteins, APM is capable of precisely modeling inter-chain interactions and designing protein complexes with binding capabilities from scratch. It also performs folding and inverse-folding tasks for multi-chain proteins. Moreover, APM demonstrates versatility in downstream applications: it achieves enhanced performance through supervised fine-tuning (SFT) while also supporting zero-shot sampling in certain tasks, achieving state-of-the-art results. Code will be released at https://github.com/bytedance/apm.
Elucidating the Design Space of Multimodal Protein Language Models
Apr 16, 2025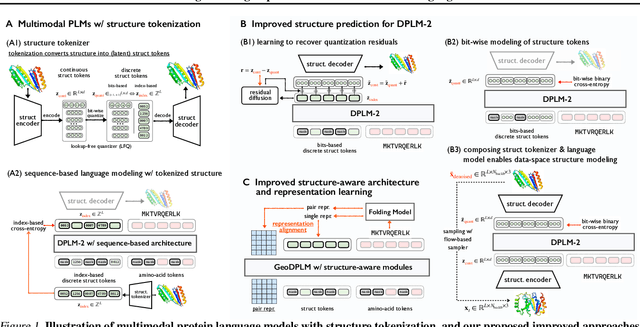
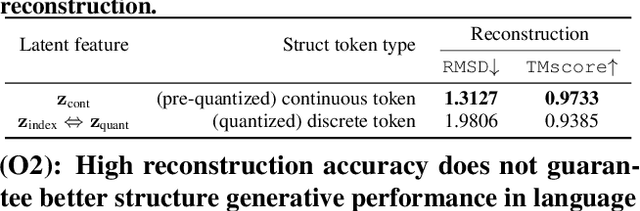
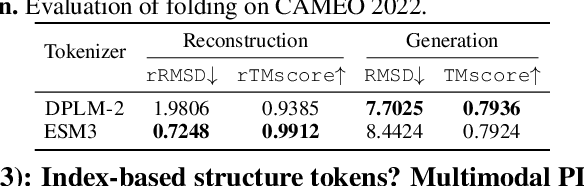
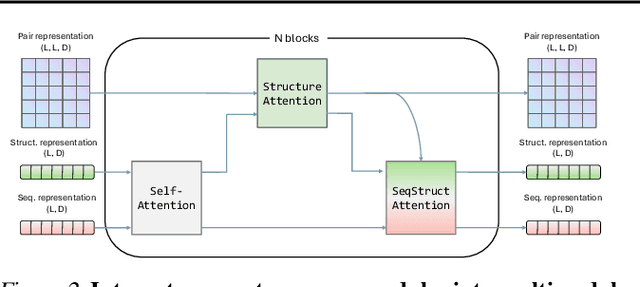
Abstract:Multimodal protein language models (PLMs) integrate sequence and token-based structural information, serving as a powerful foundation for protein modeling, generation, and design. However, the reliance on tokenizing 3D structures into discrete tokens causes substantial loss of fidelity about fine-grained structural details and correlations. In this paper, we systematically elucidate the design space of multimodal PLMs to overcome their limitations. We identify tokenization loss and inaccurate structure token predictions by the PLMs as major bottlenecks. To address these, our proposed design space covers improved generative modeling, structure-aware architectures and representation learning, and data exploration. Our advancements approach finer-grained supervision, demonstrating that token-based multimodal PLMs can achieve robust structural modeling. The effective design methods dramatically improve the structure generation diversity, and notably, folding abilities of our 650M model by reducing the RMSD from 5.52 to 2.36 on PDB testset, even outperforming 3B baselines and on par with the specialized folding models.
Variance-Dependent Regret Lower Bounds for Contextual Bandits
Mar 15, 2025Abstract:Variance-dependent regret bounds for linear contextual bandits, which improve upon the classical $\tilde{O}(d\sqrt{K})$ regret bound to $\tilde{O}(d\sqrt{\sum_{k=1}^K\sigma_k^2})$, where $d$ is the context dimension, $K$ is the number of rounds, and $\sigma^2_k$ is the noise variance in round $k$, has been widely studied in recent years. However, most existing works focus on the regret upper bounds instead of lower bounds. To our knowledge, the only lower bound is from Jia et al. (2024), which proved that for any eluder dimension $d_{\textbf{elu}}$ and total variance budget $\Lambda$, there exists an instance with $\sum_{k=1}^K\sigma_k^2\leq \Lambda$ for which any algorithm incurs a variance-dependent lower bound of $\Omega(\sqrt{d_{\textbf{elu}}\Lambda})$. However, this lower bound has a $\sqrt{d}$ gap with existing upper bounds. Moreover, it only considers a fixed total variance budget $\Lambda$ and does not apply to a general variance sequence $\{\sigma_1^2,\ldots,\sigma_K^2\}$. In this paper, to overcome the limitations of Jia et al. (2024), we consider the general variance sequence under two settings. For a prefixed sequence, where the entire variance sequence is revealed to the learner at the beginning of the learning process, we establish a variance-dependent lower bound of $\Omega(d \sqrt{\sum_{k=1}^K\sigma_k^2 }/\log K)$ for linear contextual bandits. For an adaptive sequence, where an adversary can generate the variance $\sigma_k^2$ in each round $k$ based on historical observations, we show that when the adversary must generate $\sigma_k^2$ before observing the decision set $\mathcal{D}_k$, a similar lower bound of $\Omega(d\sqrt{ \sum_{k=1}^K\sigma_k^2} /\log^6(dK))$ holds. In both settings, our results match the upper bounds of the SAVE algorithm (Zhao et al., 2023) up to logarithmic factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge