Forecast Hedging and Calibration

Calibration means that forecasts and average realized frequencies are close. We develop the concept of forecast hedging, which consists of choosing the forecasts so as to guarantee that the expected track record can only improve. This yields all the calibration results by the same simple basic argument while differentiating between them by the forecast-hedging tools used: deterministic and fixed point based versus stochastic and minimax based. Additional contributions are an improved definition of continuous calibration, ensuing game dynamics that yield Nash equilibria in the long run, and a new calibrated forecasting procedure for binary events that is simpler than all known such procedures.

Smooth Calibration, Leaky Forecasts, Finite Recall, and Nash Dynamics

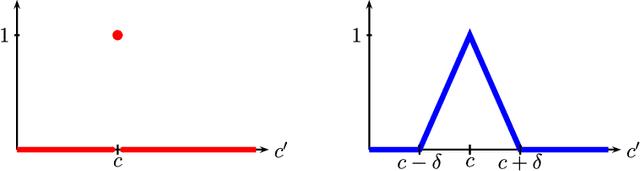
We propose to smooth out the calibration score, which measures how good a forecaster is, by combining nearby forecasts. While regular calibration can be guaranteed only by randomized forecasting procedures, we show that smooth calibration can be guaranteed by deterministic procedures. As a consequence, it does not matter if the forecasts are leaked, i.e., made known in advance: smooth calibration can nevertheless be guaranteed (while regular calibration cannot). Moreover, our procedure has finite recall, is stationary, and all forecasts lie on a finite grid. To construct the procedure, we deal also with the related setups of online linear regression and weak calibration. Finally, we show that smooth calibration yields uncoupled finite-memory dynamics in n-person games "smooth calibrated learning" in which the players play approximate Nash equilibria in almost all periods (by contrast, calibrated learning, which uses regular calibration, yields only that the time-averages of play are approximate correlated equilibria).

Calibrated Forecasts: The Minimax Proof

A formal write-up of the simple proof (1995) of the existence of calibrated forecasts by the minimax theorem, which moreover shows that N^3 periods suffice to guarantee a 1/N calibration error.

"Calibeating": Beating Forecasters at Their Own Game

In order to identify expertise, forecasters should not be tested by their calibration score, which can always be made arbitrarily small, but rather by their Brier score. The Brier score is the sum of the calibration score and the refinement score; the latter measures how good the sorting into bins with the same forecast is, and thus attests to "expertise." This raises the question of whether one can gain calibration without losing expertise, which we refer to as "calibeating." We provide an easy way to calibeat any forecast, by a deterministic online procedure. We moreover show that calibeating can be achieved by a stochastic procedure that is itself calibrated, and then extend the results to simultaneously calibeating multiple procedures, and to deterministic procedures that are continuously calibrated.