Learning to Reason with Curriculum I: Provable Benefits of Autocurriculum

Chain-of-thought reasoning, where language models expend additional computation by producing thinking tokens prior to final responses, has driven significant advances in model capabilities. However, training these reasoning models is extremely costly in terms of both data and compute, as it involves collecting long traces of reasoning behavior from humans or synthetic generators and further post-training the model via reinforcement learning. Are these costs fundamental, or can they be reduced through better algorithmic design? We show that autocurriculum, where the model uses its own performance to decide which problems to focus training on, provably improves upon standard training recipes for both supervised fine-tuning (SFT) and reinforcement learning (RL). For SFT, we show that autocurriculum requires exponentially fewer reasoning demonstrations than non-adaptive fine-tuning, by focusing teacher supervision on prompts where the current model struggles. For RL fine-tuning, autocurriculum decouples the computational cost from the quality of the reference model, reducing the latter to a burn-in cost that is nearly independent of the target accuracy. These improvements arise purely from adaptive data selection, drawing on classical techniques from boosting and learning from counterexamples, and requiring no assumption on the distribution or difficulty of prompts.

Reject, Resample, Repeat: Understanding Parallel Reasoning in Language Model Inference

Inference-time methods that aggregate and prune multiple samples have emerged as a powerful paradigm for steering large language models, yet we lack any principled understanding of their accuracy-cost tradeoffs. In this paper, we introduce a route to rigorously study such approaches using the lens of *particle filtering* algorithms such as Sequential Monte Carlo (SMC). Given a base language model and a *process reward model* estimating expected terminal rewards, we ask: *how accurately can we sample from a target distribution given some number of process reward evaluations?* Theoretically, we identify (1) simple criteria enabling non-asymptotic guarantees for SMC; (2) algorithmic improvements to SMC; and (3) a fundamental limit faced by all particle filtering methods. Empirically, we demonstrate that our theoretical criteria effectively govern the *sampling error* of SMC, though not necessarily its final *accuracy*, suggesting that theoretical perspectives beyond sampling may be necessary.

Is Best-of-N the Best of Them? Coverage, Scaling, and Optimality in Inference-Time Alignment

Inference-time computation provides an important axis for scaling language model performance, but naively scaling compute through techniques like Best-of-$N$ sampling can cause performance to degrade due to reward hacking. Toward a theoretical understanding of how to best leverage additional computation, we focus on inference-time alignment which we formalize as the problem of improving a pre-trained policy's responses for a prompt of interest, given access to an imperfect reward model. We analyze the performance of inference-time alignment algorithms in terms of (i) response quality, and (ii) compute, and provide new results that highlight the importance of the pre-trained policy's coverage over high-quality responses for performance and compute scaling: 1. We show that Best-of-$N$ alignment with an ideal choice for $N$ can achieve optimal performance under stringent notions of coverage, but provably suffers from reward hacking when $N$ is large, and fails to achieve tight guarantees under more realistic coverage conditions. 2. We introduce $\texttt{InferenceTimePessimism}$, a new algorithm which mitigates reward hacking through deliberate use of inference-time compute, implementing the principle of pessimism in the face of uncertainty via rejection sampling; we prove that its performance is optimal and does not degrade with $N$, meaning it is scaling-monotonic. We complement our theoretical results with an experimental evaluation that demonstrate the benefits of $\texttt{InferenceTimePessimism}$ across a variety of tasks and models.

Is a Good Foundation Necessary for Efficient Reinforcement Learning? The Computational Role of the Base Model in Exploration

Language model alignment (or, reinforcement learning) techniques that leverage active exploration -- deliberately encouraging the model to produce diverse, informative responses -- offer the promise of super-human capabilities. However, current understanding of algorithm design primitives for computationally efficient exploration with language models is limited. To better understand how to leverage access to powerful pre-trained generative models to improve the efficiency of exploration, we introduce a new computational framework for RL with language models, in which the learner interacts with the model through a sampling oracle. Focusing on the linear softmax model parameterization, we provide new results that reveal the computational-statistical tradeoffs of efficient exploration: 1. Necessity of coverage: Coverage refers to the extent to which the pre-trained model covers near-optimal responses -- a form of hidden knowledge. We show that coverage, while not necessary for data efficiency, lower bounds the runtime of any algorithm in our framework. 2. Inference-time exploration: We introduce a new algorithm, SpannerSampling, which obtains optimal data efficiency and is computationally efficient whenever the pre-trained model enjoys sufficient coverage, matching our lower bound. SpannerSampling leverages inference-time computation with the pre-trained model to reduce the effective search space for exploration. 3. Insufficiency of training-time interventions: We contrast the result above by showing that training-time interventions that produce proper policies cannot achieve similar guarantees in polynomial time. 4. Computational benefits of multi-turn exploration: Finally, we show that under additional representational assumptions, one can achieve improved runtime (replacing sequence-level coverage with token-level coverage) through multi-turn exploration.

Computational-Statistical Tradeoffs at the Next-Token Prediction Barrier: Autoregressive and Imitation Learning under Misspecification

Next-token prediction with the logarithmic loss is a cornerstone of autoregressive sequence modeling, but, in practice, suffers from error amplification, where errors in the model compound and generation quality degrades as sequence length $H$ increases. From a theoretical perspective, this phenomenon should not appear in well-specified settings, and, indeed, a growing body of empirical work hypothesizes that misspecification, where the learner is not sufficiently expressive to represent the target distribution, may be the root cause. Under misspecification -- where the goal is to learn as well as the best-in-class model up to a multiplicative approximation factor $C\geq 1$ -- we confirm that $C$ indeed grows with $H$ for next-token prediction, lending theoretical support to this empirical hypothesis. We then ask whether this mode of error amplification is avoidable algorithmically, computationally, or information-theoretically, and uncover inherent computational-statistical tradeoffs. We show: (1) Information-theoretically, one can avoid error amplification and achieve $C=O(1)$. (2) Next-token prediction can be made robust so as to achieve $C=\tilde O(H)$, representing moderate error amplification, but this is an inherent barrier: any next-token prediction-style objective must suffer $C=\Omega(H)$. (3) For the natural testbed of autoregressive linear models, no computationally efficient algorithm can achieve sub-polynomial approximation factor $C=e^{(\log H)^{1-\Omega(1)}}$; however, at least for binary token spaces, one can smoothly trade compute for statistical power and improve on $C=\Omega(H)$ in sub-exponential time. Our results have consequences in the more general setting of imitation learning, where the widely-used behavior cloning algorithm generalizes next-token prediction.

Necessary and Sufficient Oracles: Toward a Computational Taxonomy For Reinforcement Learning

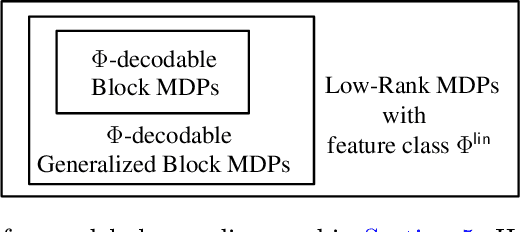
Algorithms for reinforcement learning (RL) in large state spaces crucially rely on supervised learning subroutines to estimate objects such as value functions or transition probabilities. Since only the simplest supervised learning problems can be solved provably and efficiently, practical performance of an RL algorithm depends on which of these supervised learning "oracles" it assumes access to (and how they are implemented). But which oracles are better or worse? Is there a minimal oracle? In this work, we clarify the impact of the choice of supervised learning oracle on the computational complexity of RL, as quantified by the oracle strength. First, for the task of reward-free exploration in Block MDPs in the standard episodic access model -- a ubiquitous setting for RL with function approximation -- we identify two-context regression as a minimal oracle, i.e. an oracle that is both necessary and sufficient (under a mild regularity assumption). Second, we identify one-context regression as a near-minimal oracle in the stronger reset access model, establishing a provable computational benefit of resets in the process. Third, we broaden our focus to Low-Rank MDPs, where we give cryptographic evidence that the analogous oracle from the Block MDP setting is insufficient.

Self-Improvement in Language Models: The Sharpening Mechanism

Recent work in language modeling has raised the possibility of self-improvement, where a language models evaluates and refines its own generations to achieve higher performance without external feedback. It is impossible for this self-improvement to create information that is not already in the model, so why should we expect that this will lead to improved capabilities? We offer a new perspective on the capabilities of self-improvement through a lens we refer to as sharpening. Motivated by the observation that language models are often better at verifying response quality than they are at generating correct responses, we formalize self-improvement as using the model itself as a verifier during post-training in order to ``sharpen'' the model to one placing large mass on high-quality sequences, thereby amortizing the expensive inference-time computation of generating good sequences. We begin by introducing a new statistical framework for sharpening in which the learner aims to sharpen a pre-trained base policy via sample access, and establish fundamental limits. Then we analyze two natural families of self-improvement algorithms based on SFT and RLHF.

Reinforcement Learning under Latent Dynamics: Toward Statistical and Algorithmic Modularity

Real-world applications of reinforcement learning often involve environments where agents operate on complex, high-dimensional observations, but the underlying (''latent'') dynamics are comparatively simple. However, outside of restrictive settings such as small latent spaces, the fundamental statistical requirements and algorithmic principles for reinforcement learning under latent dynamics are poorly understood. This paper addresses the question of reinforcement learning under $\textit{general}$ latent dynamics from a statistical and algorithmic perspective. On the statistical side, our main negative result shows that most well-studied settings for reinforcement learning with function approximation become intractable when composed with rich observations; we complement this with a positive result, identifying latent pushforward coverability as a general condition that enables statistical tractability. Algorithmically, we develop provably efficient observable-to-latent reductions -- that is, reductions that transform an arbitrary algorithm for the latent MDP into an algorithm that can operate on rich observations -- in two settings: one where the agent has access to hindsight observations of the latent dynamics [LADZ23], and one where the agent can estimate self-predictive latent models [SAGHCB20]. Together, our results serve as a first step toward a unified statistical and algorithmic theory for reinforcement learning under latent dynamics.

Assouad, Fano, and Le Cam with Interaction: A Unifying Lower Bound Framework and Characterization for Bandit Learnability

In this paper, we develop a unified framework for lower bound methods in statistical estimation and interactive decision making. Classical lower bound techniques -- such as Fano's inequality, Le Cam's method, and Assouad's lemma -- have been central to the study of minimax risk in statistical estimation, yet they are insufficient for the analysis of methods that collect data in an interactive manner. The recent minimax lower bounds for interactive decision making via the Decision-Estimation Coefficient (DEC) appear to be genuinely different from the classical methods. We propose a unified view of these distinct methodologies through a general algorithmic lower bound method. We further introduce a novel complexity measure, decision dimension, which facilitates the derivation of new lower bounds for interactive decision making. In particular, decision dimension provides a characterization of bandit learnability for any structured bandit model class. Further, we characterize the sample complexity of learning convex model class up to a polynomial gap with the decision dimension, addressing the remaining gap between upper and lower bounds in Foster et al. (2021, 2023).

Is Behavior Cloning All You Need? Understanding Horizon in Imitation Learning

Imitation learning (IL) aims to mimic the behavior of an expert in a sequential decision making task by learning from demonstrations, and has been widely applied to robotics, autonomous driving, and autoregressive text generation. The simplest approach to IL, behavior cloning (BC), is thought to incur sample complexity with unfavorable quadratic dependence on the problem horizon, motivating a variety of different online algorithms that attain improved linear horizon dependence under stronger assumptions on the data and the learner's access to the expert. We revisit the apparent gap between offline and online IL from a learning-theoretic perspective, with a focus on general policy classes up to and including deep neural networks. Through a new analysis of behavior cloning with the logarithmic loss, we show that it is possible to achieve horizon-independent sample complexity in offline IL whenever (i) the range of the cumulative payoffs is controlled, and (ii) an appropriate notion of supervised learning complexity for the policy class is controlled. Specializing our results to deterministic, stationary policies, we show that the gap between offline and online IL is not fundamental: (i) it is possible to achieve linear dependence on horizon in offline IL under dense rewards (matching what was previously only known to be achievable in online IL); and (ii) without further assumptions on the policy class, online IL cannot improve over offline IL with the logarithmic loss, even in benign MDPs. We complement our theoretical results with experiments on standard RL tasks and autoregressive language generation to validate the practical relevance of our findings.