BioMamba: Leveraging Spectro-Temporal Embedding in Bidirectional Mamba for Enhanced Biosignal Classification

Biological signals, such as electroencephalograms (EEGs) and electrocardiograms (ECGs), play a pivotal role in numerous clinical practices, such as diagnosing brain and cardiac arrhythmic diseases. Existing methods for biosignal classification rely on Attention-based frameworks with dense Feed Forward layers, which lead to inefficient learning, high computational overhead, and suboptimal performance. In this work, we introduce BioMamba, a Spectro-Temporal Embedding strategy applied to the Bidirectional Mamba framework with Sparse Feed Forward layers to enable effective learning of biosignal sequences. By integrating these three key components, BioMamba effectively addresses the limitations of existing methods. Extensive experiments demonstrate that BioMamba significantly outperforms state-of-the-art methods with marked improvement in classification performance. The advantages of the proposed BioMamba include (1) Reliability: BioMamba consistently delivers robust results, confirmed across six evaluation metrics. (2) Efficiency: We assess both model and training efficiency, the BioMamba demonstrates computational effectiveness by reducing model size and resource consumption compared to existing approaches. (3) Generality: With the capacity to effectively classify a diverse set of tasks, BioMamba demonstrates adaptability and effectiveness across various domains and applications.

To bootstrap or to rollout? An optimal and adaptive interpolation

Bootstrapping and rollout are two fundamental principles for value function estimation in reinforcement learning (RL). We introduce a novel class of Bellman operators, called subgraph Bellman operators, that interpolate between bootstrapping and rollout methods. Our estimator, derived by solving the fixed point of the empirical subgraph Bellman operator, combines the strengths of the bootstrapping-based temporal difference (TD) estimator and the rollout-based Monte Carlo (MC) methods. Specifically, the error upper bound of our estimator approaches the optimal variance achieved by TD, with an additional term depending on the exit probability of a selected subset of the state space. At the same time, the estimator exhibits the finite-sample adaptivity of MC, with sample complexity depending only on the occupancy measure of this subset. We complement the upper bound with an information-theoretic lower bound, showing that the additional term is unavoidable given a reasonable sample size. Together, these results establish subgraph Bellman estimators as an optimal and adaptive framework for reconciling TD and MC methods in policy evaluation.

Refined Risk Bounds for Unbounded Losses via Transductive Priors

We revisit the sequential variants of linear regression with the squared loss, classification problems with hinge loss, and logistic regression, all characterized by unbounded losses in the setup where no assumptions are made on the magnitude of design vectors and the norm of the optimal vector of parameters. The key distinction from existing results lies in our assumption that the set of design vectors is known in advance (though their order is not), a setup sometimes referred to as transductive online learning. While this assumption seems similar to fixed design regression or denoising, we demonstrate that the sequential nature of our algorithms allows us to convert our bounds into statistical ones with random design without making any additional assumptions about the distribution of the design vectors--an impossibility for standard denoising results. Our key tools are based on the exponential weights algorithm with carefully chosen transductive (design-dependent) priors, which exploit the full horizon of the design vectors. Our classification regret bounds have a feature that is only attributed to bounded losses in the literature: they depend solely on the dimension of the parameter space and on the number of rounds, independent of the design vectors or the norm of the optimal solution. For linear regression with squared loss, we further extend our analysis to the sparse case, providing sparsity regret bounds that additionally depend on the magnitude of the response variables. We argue that these improved bounds are specific to the transductive setting and unattainable in the worst-case sequential setup. Our algorithms, in several cases, have polynomial time approximations and reduce to sampling with respect to log-concave measures instead of aggregating over hard-to-construct $\varepsilon$-covers of classes.

How Does Variance Shape the Regret in Contextual Bandits?

We consider realizable contextual bandits with general function approximation, investigating how small reward variance can lead to better-than-minimax regret bounds. Unlike in minimax bounds, we show that the eluder dimension $d_\text{elu}$$-$a complexity measure of the function class$-$plays a crucial role in variance-dependent bounds. We consider two types of adversary: (1) Weak adversary: The adversary sets the reward variance before observing the learner's action. In this setting, we prove that a regret of $\Omega(\sqrt{\min\{A,d_\text{elu}\}\Lambda}+d_\text{elu})$ is unavoidable when $d_{\text{elu}}\leq\sqrt{AT}$, where $A$ is the number of actions, $T$ is the total number of rounds, and $\Lambda$ is the total variance over $T$ rounds. For the $A\leq d_\text{elu}$ regime, we derive a nearly matching upper bound $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$ for the special case where the variance is revealed at the beginning of each round. (2) Strong adversary: The adversary sets the reward variance after observing the learner's action. We show that a regret of $\Omega(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ is unavoidable when $\sqrt{d_\text{elu}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. In this setting, we provide an upper bound of order $\tilde{O}(d_\text{elu}\sqrt{\Lambda}+d_\text{elu})$. Furthermore, we examine the setting where the function class additionally provides distributional information of the reward, as studied by Wang et al. (2024). We demonstrate that the regret bound $\tilde{O}(\sqrt{d_\text{elu}\Lambda}+d_\text{elu})$ established in their work is unimprovable when $\sqrt{d_{\text{elu}}\Lambda}+d_\text{elu}\leq\sqrt{AT}$. However, with a slightly different definition of the total variance and with the assumption that the reward follows a Gaussian distribution, one can achieve a regret of $\tilde{O}(\sqrt{A\Lambda}+d_\text{elu})$.

Assouad, Fano, and Le Cam with Interaction: A Unifying Lower Bound Framework and Characterization for Bandit Learnability

In this paper, we develop a unified framework for lower bound methods in statistical estimation and interactive decision making. Classical lower bound techniques -- such as Fano's inequality, Le Cam's method, and Assouad's lemma -- have been central to the study of minimax risk in statistical estimation, yet they are insufficient for the analysis of methods that collect data in an interactive manner. The recent minimax lower bounds for interactive decision making via the Decision-Estimation Coefficient (DEC) appear to be genuinely different from the classical methods. We propose a unified view of these distinct methodologies through a general algorithmic lower bound method. We further introduce a novel complexity measure, decision dimension, which facilitates the derivation of new lower bounds for interactive decision making. In particular, decision dimension provides a characterization of bandit learnability for any structured bandit model class. Further, we characterize the sample complexity of learning convex model class up to a polynomial gap with the decision dimension, addressing the remaining gap between upper and lower bounds in Foster et al. (2021, 2023).

SDformer: Efficient End-to-End Transformer for Depth Completion

Depth completion aims to predict dense depth maps with sparse depth measurements from a depth sensor. Currently, Convolutional Neural Network (CNN) based models are the most popular methods applied to depth completion tasks. However, despite the excellent high-end performance, they suffer from a limited representation area. To overcome the drawbacks of CNNs, a more effective and powerful method has been presented: the Transformer, which is an adaptive self-attention setting sequence-to-sequence model. While the standard Transformer quadratically increases the computational cost from the key-query dot-product of input resolution which improperly employs depth completion tasks. In this work, we propose a different window-based Transformer architecture for depth completion tasks named Sparse-to-Dense Transformer (SDformer). The network consists of an input module for the depth map and RGB image features extraction and concatenation, a U-shaped encoder-decoder Transformer for extracting deep features, and a refinement module. Specifically, we first concatenate the depth map features with the RGB image features through the input model. Then, instead of calculating self-attention with the whole feature maps, we apply different window sizes to extract the long-range depth dependencies. Finally, we refine the predicted features from the input module and the U-shaped encoder-decoder Transformer module to get the enriching depth features and employ a convolution layer to obtain the dense depth map. In practice, the SDformer obtains state-of-the-art results against the CNN-based depth completion models with lower computing loads and parameters on the NYU Depth V2 and KITTI DC datasets.

Sub-SA: Strengthen In-context Learning via Submodular Selective Annotation

In-context learning (ICL) leverages in-context examples as prompts for the predictions of Large Language Models (LLMs). These prompts play a crucial role in achieving strong performance. However, the selection of suitable prompts from a large pool of labeled examples often entails significant annotation costs. To address this challenge, we propose \textbf{Sub-SA} (\textbf{Sub}modular \textbf{S}elective \textbf{A}nnotation), a submodule-based selective annotation method. The aim of Sub-SA is to reduce annotation costs while improving the quality of in-context examples and minimizing the time consumption of the selection process. In Sub-SA, we design a submodular function that facilitates effective subset selection for annotation and demonstrates the characteristics of monotonically and submodularity from the theoretical perspective. Specifically, we propose \textbf{RPR} (\textbf{R}eward and \textbf{P}enalty \textbf{R}egularization) to better balance the diversity and representativeness of the unlabeled dataset attributed to a reward term and a penalty term, respectively. Consequently, the selection for annotations can be effectively addressed with a simple yet effective greedy search algorithm based on the submodular function. Finally, we apply the similarity prompt retrieval to get the examples for ICL.

TimeLDM: Latent Diffusion Model for Unconditional Time Series Generation

Time series generation is a crucial research topic in the area of deep learning, which can be used for data augmentation, imputing missing values, and forecasting. Currently, latent diffusion models are ascending to the forefront of generative modeling for many important data representations. Being the most pivotal in the computer vision domain, latent diffusion models have also recently attracted interest in other communities, including NLP, Speech, and Geometric Space. In this work, we propose TimeLDM, a novel latent diffusion model for high-quality time series generation. TimeLDM is composed of a variational autoencoder that encodes time series into an informative and smoothed latent content and a latent diffusion model operating in the latent space to generate latent information. We evaluate the ability of our method to generate synthetic time series with simulated and realistic datasets, benchmark the performance against existing state-of-the-art methods. Qualitatively and quantitatively, we find that the proposed TimeLDM persistently delivers high-quality generated time series. Sores from Context-FID and Discriminative indicate that TimeLDM consistently and significantly outperforms current state-of-the-art benchmarks with an average improvement of 3.4$\times$ and 3.8$\times$, respectively. Further studies demonstrate that our method presents better performance on different lengths of time series data generation. To the best of our knowledge, this is the first study to explore the potential of the latent diffusion model for unconditional time series generation and establish a new baseline for synthetic time series.

Offline Oracle-Efficient Learning for Contextual MDPs via Layerwise Exploration-Exploitation Tradeoff

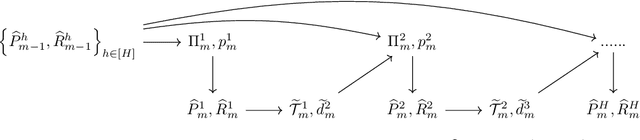
Motivated by the recent discovery of a statistical and computational reduction from contextual bandits to offline regression (Simchi-Levi and Xu, 2021), we address the general (stochastic) Contextual Markov Decision Process (CMDP) problem with horizon H (as known as CMDP with H layers). In this paper, we introduce a reduction from CMDPs to offline density estimation under the realizability assumption, i.e., a model class M containing the true underlying CMDP is provided in advance. We develop an efficient, statistically near-optimal algorithm requiring only O(HlogT) calls to an offline density estimation algorithm (or oracle) across all T rounds of interaction. This number can be further reduced to O(HloglogT) if T is known in advance. Our results mark the first efficient and near-optimal reduction from CMDPs to offline density estimation without imposing any structural assumptions on the model class. A notable feature of our algorithm is the design of a layerwise exploration-exploitation tradeoff tailored to address the layerwise structure of CMDPs. Additionally, our algorithm is versatile and applicable to pure exploration tasks in reward-free reinforcement learning.

Online Estimation via Offline Estimation: An Information-Theoretic Framework

$ $The classical theory of statistical estimation aims to estimate a parameter of interest under data generated from a fixed design ("offline estimation"), while the contemporary theory of online learning provides algorithms for estimation under adaptively chosen covariates ("online estimation"). Motivated by connections between estimation and interactive decision making, we ask: is it possible to convert offline estimation algorithms into online estimation algorithms in a black-box fashion? We investigate this question from an information-theoretic perspective by introducing a new framework, Oracle-Efficient Online Estimation (OEOE), where the learner can only interact with the data stream indirectly through a sequence of offline estimators produced by a black-box algorithm operating on the stream. Our main results settle the statistical and computational complexity of online estimation in this framework. $\bullet$ Statistical complexity. We show that information-theoretically, there exist algorithms that achieve near-optimal online estimation error via black-box offline estimation oracles, and give a nearly-tight characterization for minimax rates in the OEOE framework. $\bullet$ Computational complexity. We show that the guarantees above cannot be achieved in a computationally efficient fashion in general, but give a refined characterization for the special case of conditional density estimation: computationally efficient online estimation via black-box offline estimation is possible whenever it is possible via unrestricted algorithms. Finally, we apply our results to give offline oracle-efficient algorithms for interactive decision making.