A Simplified Analysis of SGD for Linear Regression with Weight Averaging

Theoretically understanding stochastic gradient descent (SGD) in overparameterized models has led to the development of several optimization algorithms that are widely used in practice today. Recent work by~\citet{zou2021benign} provides sharp rates for SGD optimization in linear regression using constant learning rate, both with and without tail iterate averaging, based on a bias-variance decomposition of the risk. In our work, we provide a simplified analysis recovering the same bias and variance bounds provided in~\citep{zou2021benign} based on simple linear algebra tools, bypassing the requirement to manipulate operators on positive semi-definite (PSD) matrices. We believe our work makes the analysis of SGD on linear regression very accessible and will be helpful in further analyzing mini-batching and learning rate scheduling, leading to improvements in the training of realistic models.

Improved Scaling Laws in Linear Regression via Data Reuse

Neural scaling laws suggest that the test error of large language models trained online decreases polynomially as the model size and data size increase. However, such scaling can be unsustainable when running out of new data. In this work, we show that data reuse can improve existing scaling laws in linear regression. Specifically, we derive sharp test error bounds on $M$-dimensional linear models trained by multi-pass stochastic gradient descent (multi-pass SGD) on $N$ data with sketched features. Assuming that the data covariance has a power-law spectrum of degree $a$, and that the true parameter follows a prior with an aligned power-law spectrum of degree $b-a$ (with $a > b > 1$), we show that multi-pass SGD achieves a test error of $\Theta(M^{1-b} + L^{(1-b)/a})$, where $L \lesssim N^{a/b}$ is the number of iterations. In the same setting, one-pass SGD only attains a test error of $\Theta(M^{1-b} + N^{(1-b)/a})$ (see e.g., Lin et al., 2024). This suggests an improved scaling law via data reuse (i.e., choosing $L>N$) in data-constrained regimes. Numerical simulations are also provided to verify our theoretical findings.

Memory-Statistics Tradeoff in Continual Learning with Structural Regularization

We study the statistical performance of a continual learning problem with two linear regression tasks in a well-specified random design setting. We consider a structural regularization algorithm that incorporates a generalized $\ell_2$-regularization tailored to the Hessian of the previous task for mitigating catastrophic forgetting. We establish upper and lower bounds on the joint excess risk for this algorithm. Our analysis reveals a fundamental trade-off between memory complexity and statistical efficiency, where memory complexity is measured by the number of vectors needed to define the structural regularization. Specifically, increasing the number of vectors in structural regularization leads to a worse memory complexity but an improved excess risk, and vice versa. Furthermore, our theory suggests that naive continual learning without regularization suffers from catastrophic forgetting, while structural regularization mitigates this issue. Notably, structural regularization achieves comparable performance to joint training with access to both tasks simultaneously. These results highlight the critical role of curvature-aware regularization for continual learning.

Minimax Optimal Convergence of Gradient Descent in Logistic Regression via Large and Adaptive Stepsizes

We study $\textit{gradient descent}$ (GD) for logistic regression on linearly separable data with stepsizes that adapt to the current risk, scaled by a constant hyperparameter $\eta$. We show that after at most $1/\gamma^2$ burn-in steps, GD achieves a risk upper bounded by $\exp(-\Theta(\eta))$, where $\gamma$ is the margin of the dataset. As $\eta$ can be arbitrarily large, GD attains an arbitrarily small risk $\textit{immediately after the burn-in steps}$, though the risk evolution may be $\textit{non-monotonic}$. We further construct hard datasets with margin $\gamma$, where any batch or online first-order method requires $\Omega(1/\gamma^2)$ steps to find a linear separator. Thus, GD with large, adaptive stepsizes is $\textit{minimax optimal}$ among first-order batch methods. Notably, the classical $\textit{Perceptron}$ (Novikoff, 1962), a first-order online method, also achieves a step complexity of $1/\gamma^2$, matching GD even in constants. Finally, our GD analysis extends to a broad class of loss functions and certain two-layer networks.

Implicit Bias of Gradient Descent for Non-Homogeneous Deep Networks

We establish the asymptotic implicit bias of gradient descent (GD) for generic non-homogeneous deep networks under exponential loss. Specifically, we characterize three key properties of GD iterates starting from a sufficiently small empirical risk, where the threshold is determined by a measure of the network's non-homogeneity. First, we show that a normalized margin induced by the GD iterates increases nearly monotonically. Second, we prove that while the norm of the GD iterates diverges to infinity, the iterates themselves converge in direction. Finally, we establish that this directional limit satisfies the Karush-Kuhn-Tucker (KKT) conditions of a margin maximization problem. Prior works on implicit bias have focused exclusively on homogeneous networks; in contrast, our results apply to a broad class of non-homogeneous networks satisfying a mild near-homogeneity condition. In particular, our results apply to networks with residual connections and non-homogeneous activation functions, thereby resolving an open problem posed by Ji and Telgarsky (2020).

Benefits of Early Stopping in Gradient Descent for Overparameterized Logistic Regression

In overparameterized logistic regression, gradient descent (GD) iterates diverge in norm while converging in direction to the maximum $\ell_2$-margin solution -- a phenomenon known as the implicit bias of GD. This work investigates additional regularization effects induced by early stopping in well-specified high-dimensional logistic regression. We first demonstrate that the excess logistic risk vanishes for early-stopped GD but diverges to infinity for GD iterates at convergence. This suggests that early-stopped GD is well-calibrated, whereas asymptotic GD is statistically inconsistent. Second, we show that to attain a small excess zero-one risk, polynomially many samples are sufficient for early-stopped GD, while exponentially many samples are necessary for any interpolating estimator, including asymptotic GD. This separation underscores the statistical benefits of early stopping in the overparameterized regime. Finally, we establish nonasymptotic bounds on the norm and angular differences between early-stopped GD and $\ell_2$-regularized empirical risk minimizer, thereby connecting the implicit regularization of GD with explicit $\ell_2$-regularization.

How Does Critical Batch Size Scale in Pre-training?

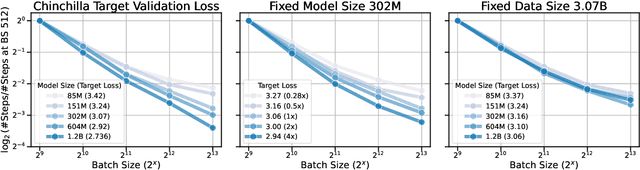
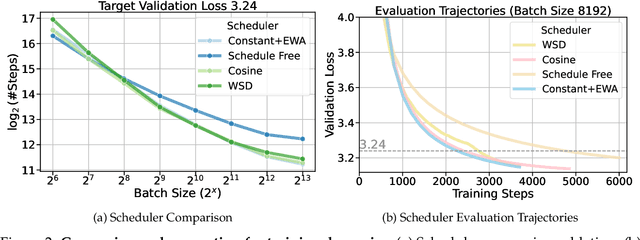
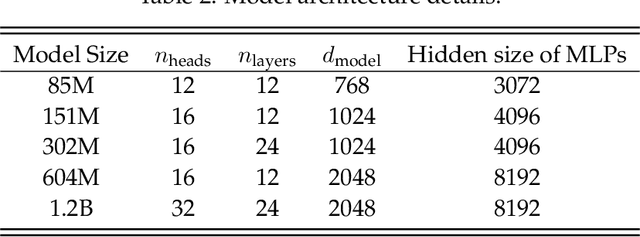
Training large-scale models under given resources requires careful design of parallelism strategies. In particular, the efficiency notion of critical batch size, concerning the compromise between time and compute, marks the threshold beyond which greater data parallelism leads to diminishing returns. To operationalize it, we propose a measure of CBS and pre-train a series of auto-regressive language models, ranging from 85 million to 1.2 billion parameters, on the C4 dataset. Through extensive hyper-parameter sweeps and careful control on factors such as batch size, momentum, and learning rate along with its scheduling, we systematically investigate the impact of scale on CBS. Then we fit scaling laws with respect to model and data sizes to decouple their effects. Overall, our results demonstrate that CBS scales primarily with data size rather than model size, a finding we justify theoretically through the analysis of infinite-width limits of neural networks and infinite-dimensional least squares regression. Of independent interest, we highlight the importance of common hyper-parameter choices and strategies for studying large-scale pre-training beyond fixed training durations.

Context-Scaling versus Task-Scaling in In-Context Learning

Transformers exhibit In-Context Learning (ICL), where these models solve new tasks by using examples in the prompt without additional training. In our work, we identify and analyze two key components of ICL: (1) context-scaling, where model performance improves as the number of in-context examples increases and (2) task-scaling, where model performance improves as the number of pre-training tasks increases. While transformers are capable of both context-scaling and task-scaling, we empirically show that standard Multi-Layer Perceptrons (MLPs) with vectorized input are only capable of task-scaling. To understand how transformers are capable of context-scaling, we first propose a significantly simplified transformer architecture without key, query, value weights. We show that it performs ICL comparably to the original GPT-2 model in various statistical learning tasks including linear regression, teacher-student settings. Furthermore, a single block of our simplified transformer can be viewed as data dependent feature map followed by an MLP. This feature map on its own is a powerful predictor that is capable of context-scaling but is not capable of task-scaling. We show empirically that concatenating the output of this feature map with vectorized data as an input to MLPs enables both context-scaling and task-scaling. This finding provides a simple setting to study context and task-scaling for ICL.

Large Stepsize Gradient Descent for Non-Homogeneous Two-Layer Networks: Margin Improvement and Fast Optimization

The typical training of neural networks using large stepsize gradient descent (GD) under the logistic loss often involves two distinct phases, where the empirical risk oscillates in the first phase but decreases monotonically in the second phase. We investigate this phenomenon in two-layer networks that satisfy a near-homogeneity condition. We show that the second phase begins once the empirical risk falls below a certain threshold, dependent on the stepsize. Additionally, we show that the normalized margin grows nearly monotonically in the second phase, demonstrating an implicit bias of GD in training non-homogeneous predictors. If the dataset is linearly separable and the derivative of the activation function is bounded away from zero, we show that the average empirical risk decreases, implying that the first phase must stop in finite steps. Finally, we demonstrate that by choosing a suitably large stepsize, GD that undergoes this phase transition is more efficient than GD that monotonically decreases the risk. Our analysis applies to networks of any width, beyond the well-known neural tangent kernel and mean-field regimes.

Scaling Laws in Linear Regression: Compute, Parameters, and Data

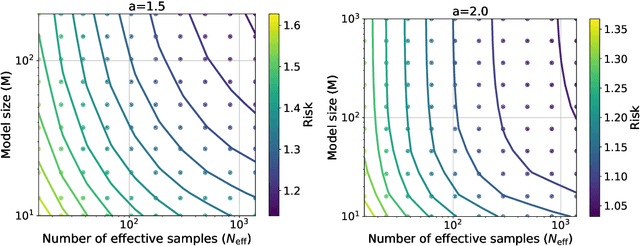
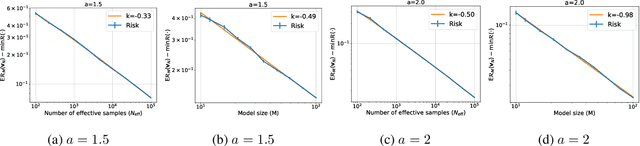
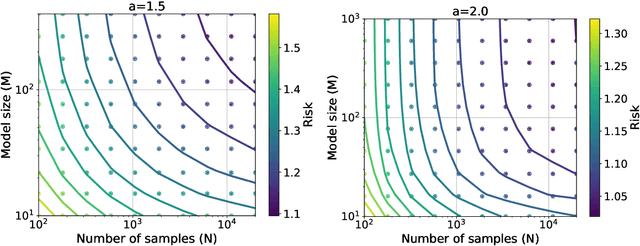
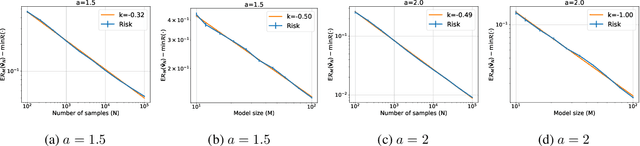
Empirically, large-scale deep learning models often satisfy a neural scaling law: the test error of the trained model improves polynomially as the model size and data size grow. However, conventional wisdom suggests the test error consists of approximation, bias, and variance errors, where the variance error increases with model size. This disagrees with the general form of neural scaling laws, which predict that increasing model size monotonically improves performance. We study the theory of scaling laws in an infinite dimensional linear regression setup. Specifically, we consider a model with $M$ parameters as a linear function of sketched covariates. The model is trained by one-pass stochastic gradient descent (SGD) using $N$ data. Assuming the optimal parameter satisfies a Gaussian prior and the data covariance matrix has a power-law spectrum of degree $a>1$, we show that the reducible part of the test error is $\Theta(M^{-(a-1)} + N^{-(a-1)/a})$. The variance error, which increases with $M$, is dominated by the other errors due to the implicit regularization of SGD, thus disappearing from the bound. Our theory is consistent with the empirical neural scaling laws and verified by numerical simulation.