The Potential of Second-Order Optimization for LLMs: A Study with Full Gauss-Newton

Recent efforts to accelerate LLM pretraining have focused on computationally-efficient approximations that exploit second-order structure. This raises a key question for large-scale training: how much performance is forfeited by these approximations? To probe this question, we establish a practical upper bound on iteration complexity by applying full Gauss-Newton (GN) preconditioning to transformer models of up to 150M parameters. Our experiments show that full GN updates yield substantial gains over existing optimizers, achieving a 5.4x reduction in training iterations compared to strong baselines like SOAP and Muon. Furthermore, we find that a precise layerwise GN preconditioner, which ignores cross-layer information, nearly matches the performance of the full GN method. Collectively, our results suggest: (1) the GN approximation is highly effective for preconditioning, implying higher-order loss terms may not be critical for convergence speed; (2) the layerwise Hessian structure contains sufficient information to achieve most of these potential gains; and (3) a significant performance gap exists between current approximate methods and an idealized layerwise oracle.

Connections between Schedule-Free Optimizers, AdEMAMix, and Accelerated SGD Variants

Recent advancements in deep learning optimization have introduced new algorithms, such as Schedule-Free optimizers, AdEMAMix, MARS and Lion which modify traditional momentum mechanisms. In a separate line of work, theoretical acceleration of stochastic gradient descent (SGD) in noise-dominated regime has been achieved by decoupling the momentum coefficient from the current gradient's weight. In this paper, we establish explicit connections between these two lines of work. We substantiate our theoretical findings with preliminary experiments on a 150m language modeling task. We find that AdEMAMix, which most closely resembles accelerated versions of stochastic gradient descent, exhibits superior performance. Building on these insights, we introduce a modification to AdEMAMix, termed Simplified-AdEMAMix, which maintains the same performance as AdEMAMix across both large and small batch-size settings while eliminating the need for two different momentum terms. The code for Simplified-AdEMAMix is available on the repository: https://github.com/DepenM/Simplified-AdEMAMix/.

Loss-to-Loss Prediction: Scaling Laws for All Datasets

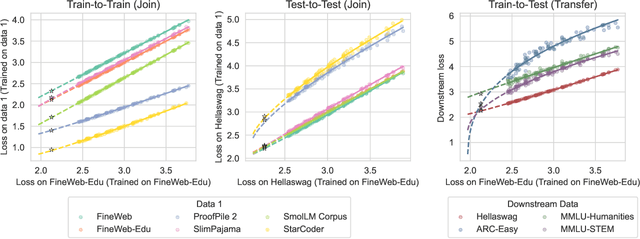
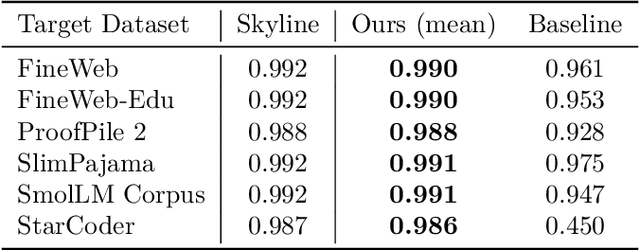
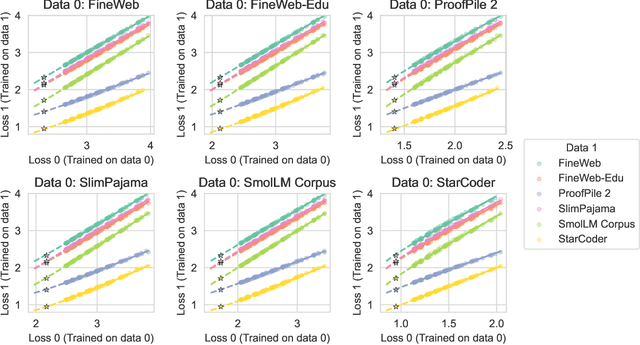
While scaling laws provide a reliable methodology for predicting train loss across compute scales for a single data distribution, less is known about how these predictions should change as we change the distribution. In this paper, we derive a strategy for predicting one loss from another and apply it to predict across different pre-training datasets and from pre-training data to downstream task data. Our predictions extrapolate well even at 20x the largest FLOP budget used to fit the curves. More precisely, we find that there are simple shifted power law relationships between (1) the train losses of two models trained on two separate datasets when the models are paired by training compute (train-to-train), (2) the train loss and the test loss on any downstream distribution for a single model (train-to-test), and (3) the test losses of two models trained on two separate train datasets (test-to-test). The results hold up for pre-training datasets that differ substantially (some are entirely code and others have no code at all) and across a variety of downstream tasks. Finally, we find that in some settings these shifted power law relationships can yield more accurate predictions than extrapolating single-dataset scaling laws.

How Does Critical Batch Size Scale in Pre-training?

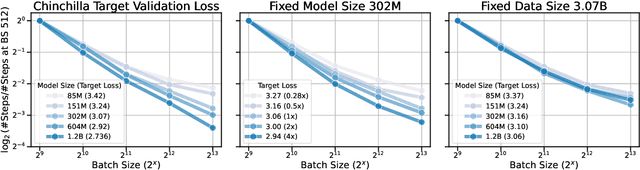
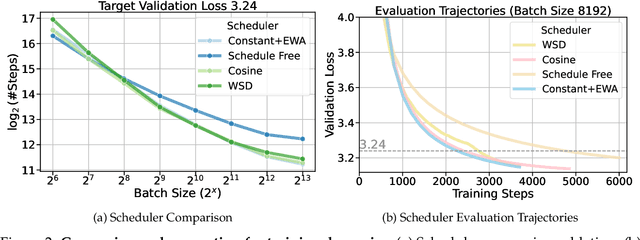
Training large-scale models under given resources requires careful design of parallelism strategies. In particular, the efficiency notion of critical batch size, concerning the compromise between time and compute, marks the threshold beyond which greater data parallelism leads to diminishing returns. To operationalize it, we propose a measure of CBS and pre-train a series of auto-regressive language models, ranging from 85 million to 1.2 billion parameters, on the C4 dataset. Through extensive hyper-parameter sweeps and careful control on factors such as batch size, momentum, and learning rate along with its scheduling, we systematically investigate the impact of scale on CBS. Then we fit scaling laws with respect to model and data sizes to decouple their effects. Overall, our results demonstrate that CBS scales primarily with data size rather than model size, a finding we justify theoretically through the analysis of infinite-width limits of neural networks and infinite-dimensional least squares regression. Of independent interest, we highlight the importance of common hyper-parameter choices and strategies for studying large-scale pre-training beyond fixed training durations.

Mixture of Parrots: Experts improve memorization more than reasoning

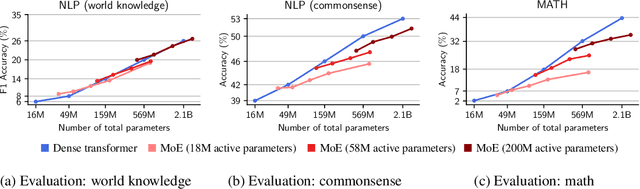
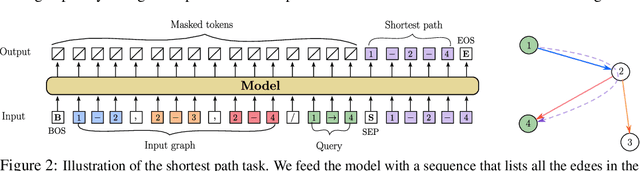
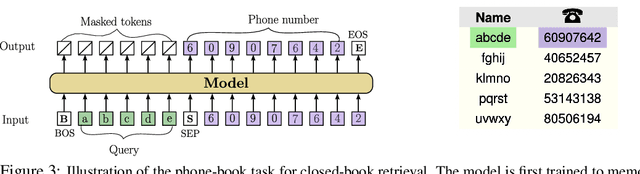
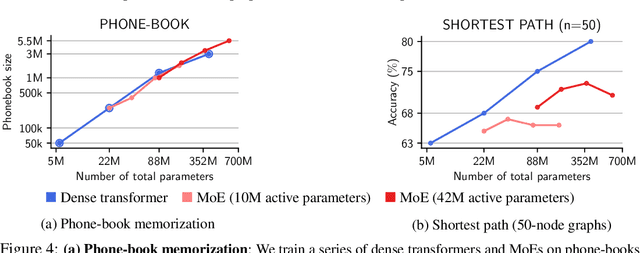
The Mixture-of-Experts (MoE) architecture enables a significant increase in the total number of model parameters with minimal computational overhead. However, it is not clear what performance tradeoffs, if any, exist between MoEs and standard dense transformers. In this paper, we show that as we increase the number of experts (while fixing the number of active parameters), the memorization performance consistently increases while the reasoning capabilities saturate. We begin by analyzing the theoretical limitations of MoEs at reasoning. We prove that there exist graph problems that cannot be solved by any number of experts of a certain width; however, the same task can be easily solved by a dense model with a slightly larger width. On the other hand, we find that on memory-intensive tasks, MoEs can effectively leverage a small number of active parameters with a large number of experts to memorize the data. We empirically validate these findings on synthetic graph problems and memory-intensive closed book retrieval tasks. Lastly, we pre-train a series of MoEs and dense transformers and evaluate them on commonly used benchmarks in math and natural language. We find that increasing the number of experts helps solve knowledge-intensive tasks, but fails to yield the same benefits for reasoning tasks.

SOAP: Improving and Stabilizing Shampoo using Adam

There is growing evidence of the effectiveness of Shampoo, a higher-order preconditioning method, over Adam in deep learning optimization tasks. However, Shampoo's drawbacks include additional hyperparameters and computational overhead when compared to Adam, which only updates running averages of first- and second-moment quantities. This work establishes a formal connection between Shampoo (implemented with the 1/2 power) and Adafactor -- a memory-efficient approximation of Adam -- showing that Shampoo is equivalent to running Adafactor in the eigenbasis of Shampoo's preconditioner. This insight leads to the design of a simpler and computationally efficient algorithm: $\textbf{S}$hampo$\textbf{O}$ with $\textbf{A}$dam in the $\textbf{P}$reconditioner's eigenbasis (SOAP). With regards to improving Shampoo's computational efficiency, the most straightforward approach would be to simply compute Shampoo's eigendecomposition less frequently. Unfortunately, as our empirical results show, this leads to performance degradation that worsens with this frequency. SOAP mitigates this degradation by continually updating the running average of the second moment, just as Adam does, but in the current (slowly changing) coordinate basis. Furthermore, since SOAP is equivalent to running Adam in a rotated space, it introduces only one additional hyperparameter (the preconditioning frequency) compared to Adam. We empirically evaluate SOAP on language model pre-training with 360m and 660m sized models. In the large batch regime, SOAP reduces the number of iterations by over 40% and wall clock time by over 35% compared to AdamW, with approximately 20% improvements in both metrics compared to Shampoo. An implementation of SOAP is available at https://github.com/nikhilvyas/SOAP.

Deconstructing What Makes a Good Optimizer for Language Models

Training language models becomes increasingly expensive with scale, prompting numerous attempts to improve optimization efficiency. Despite these efforts, the Adam optimizer remains the most widely used, due to a prevailing view that it is the most effective approach. We aim to compare several optimization algorithms, including SGD, Adafactor, Adam, and Lion, in the context of autoregressive language modeling across a range of model sizes, hyperparameters, and architecture variants. Our findings indicate that, except for SGD, these algorithms all perform comparably both in their optimal performance and also in terms of how they fare across a wide range of hyperparameter choices. Our results suggest to practitioners that the choice of optimizer can be guided by practical considerations like memory constraints and ease of implementation, as no single algorithm emerged as a clear winner in terms of performance or stability to hyperparameter misspecification. Given our findings, we further dissect these approaches, examining two simplified versions of Adam: a) signed momentum (Signum) which we see recovers both the performance and hyperparameter stability of Adam and b) Adalayer, a layerwise variant of Adam which we introduce to study Adam's preconditioning. Examining Adalayer leads us to the conclusion that the largest impact of Adam's preconditioning is restricted to the last layer and LayerNorm parameters, and, perhaps surprisingly, the remaining layers can be trained with SGD.

A New Perspective on Shampoo's Preconditioner

Shampoo, a second-order optimization algorithm which uses a Kronecker product preconditioner, has recently garnered increasing attention from the machine learning community. The preconditioner used by Shampoo can be viewed either as an approximation of the Gauss--Newton component of the Hessian or the covariance matrix of the gradients maintained by Adagrad. We provide an explicit and novel connection between the $\textit{optimal}$ Kronecker product approximation of these matrices and the approximation made by Shampoo. Our connection highlights a subtle but common misconception about Shampoo's approximation. In particular, the $\textit{square}$ of the approximation used by the Shampoo optimizer is equivalent to a single step of the power iteration algorithm for computing the aforementioned optimal Kronecker product approximation. Across a variety of datasets and architectures we empirically demonstrate that this is close to the optimal Kronecker product approximation. Additionally, for the Hessian approximation viewpoint, we empirically study the impact of various practical tricks to make Shampoo more computationally efficient (such as using the batch gradient and the empirical Fisher) on the quality of Hessian approximation.

Distinguishing the Knowable from the Unknowable with Language Models

We study the feasibility of identifying epistemic uncertainty (reflecting a lack of knowledge), as opposed to aleatoric uncertainty (reflecting entropy in the underlying distribution), in the outputs of large language models (LLMs) over free-form text. In the absence of ground-truth probabilities, we explore a setting where, in order to (approximately) disentangle a given LLM's uncertainty, a significantly larger model stands in as a proxy for the ground truth. We show that small linear probes trained on the embeddings of frozen, pretrained models accurately predict when larger models will be more confident at the token level and that probes trained on one text domain generalize to others. Going further, we propose a fully unsupervised method that achieves non-trivial accuracy on the same task. Taken together, we interpret these results as evidence that LLMs naturally contain internal representations of different types of uncertainty that could potentially be leveraged to devise more informative indicators of model confidence in diverse practical settings.

On Privileged and Convergent Bases in Neural Network Representations

In this study, we investigate whether the representations learned by neural networks possess a privileged and convergent basis. Specifically, we examine the significance of feature directions represented by individual neurons. First, we establish that arbitrary rotations of neural representations cannot be inverted (unlike linear networks), indicating that they do not exhibit complete rotational invariance. Subsequently, we explore the possibility of multiple bases achieving identical performance. To do this, we compare the bases of networks trained with the same parameters but with varying random initializations. Our study reveals two findings: (1) Even in wide networks such as WideResNets, neural networks do not converge to a unique basis; (2) Basis correlation increases significantly when a few early layers of the network are frozen identically. Furthermore, we analyze Linear Mode Connectivity, which has been studied as a measure of basis correlation. Our findings give evidence that while Linear Mode Connectivity improves with increased network width, this improvement is not due to an increase in basis correlation.