Structure-Informed Deep Reinforcement Learning for Inventory Management

This paper investigates the application of Deep Reinforcement Learning (DRL) to classical inventory management problems, with a focus on practical implementation considerations. We apply a DRL algorithm based on DirectBackprop to several fundamental inventory management scenarios including multi-period systems with lost sales (with and without lead times), perishable inventory management, dual sourcing, and joint inventory procurement and removal. The DRL approach learns policies across products using only historical information that would be available in practice, avoiding unrealistic assumptions about demand distributions or access to distribution parameters. We demonstrate that our generic DRL implementation performs competitively against or outperforms established benchmarks and heuristics across these diverse settings, while requiring minimal parameter tuning. Through examination of the learned policies, we show that the DRL approach naturally captures many known structural properties of optimal policies derived from traditional operations research methods. To further improve policy performance and interpretability, we propose a Structure-Informed Policy Network technique that explicitly incorporates analytically-derived characteristics of optimal policies into the learning process. This approach can help interpretability and add robustness to the policy in out-of-sample performance, as we demonstrate in an example with realistic demand data. Finally, we provide an illustrative application of DRL in a non-stationary setting. Our work bridges the gap between data-driven learning and analytical insights in inventory management while maintaining practical applicability.

Mind the Gap: Examining the Self-Improvement Capabilities of Large Language Models

Self-improvement is a mechanism in Large Language Model (LLM) pre-training, post-training and test-time inference. We explore a framework where the model verifies its own outputs, filters or reweights data based on this verification, and distills the filtered data. Despite several empirical successes, a fundamental understanding is still lacking. In this work, we initiate a comprehensive, modular and controlled study on LLM self-improvement. We provide a mathematical formulation for self-improvement, which is largely governed by a quantity which we formalize as the generation-verification gap. Through experiments with various model families and tasks, we discover a scaling phenomenon of self-improvement -- a variant of the generation-verification gap scales monotonically with the model pre-training flops. We also examine when self-improvement is possible, an iterative self-improvement procedure, and ways to improve its performance. Our findings not only advance understanding of LLM self-improvement with practical implications, but also open numerous avenues for future research into its capabilities and boundaries.

How Does Critical Batch Size Scale in Pre-training?

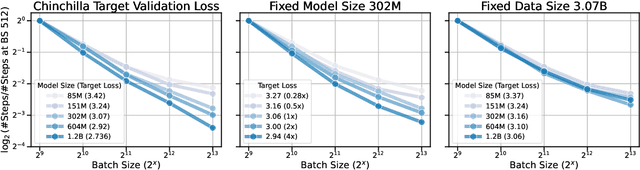
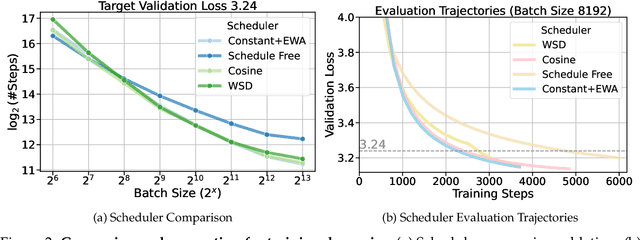
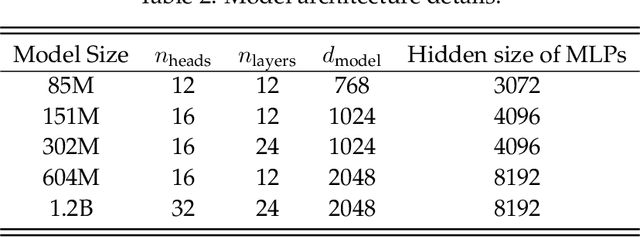
Training large-scale models under given resources requires careful design of parallelism strategies. In particular, the efficiency notion of critical batch size, concerning the compromise between time and compute, marks the threshold beyond which greater data parallelism leads to diminishing returns. To operationalize it, we propose a measure of CBS and pre-train a series of auto-regressive language models, ranging from 85 million to 1.2 billion parameters, on the C4 dataset. Through extensive hyper-parameter sweeps and careful control on factors such as batch size, momentum, and learning rate along with its scheduling, we systematically investigate the impact of scale on CBS. Then we fit scaling laws with respect to model and data sizes to decouple their effects. Overall, our results demonstrate that CBS scales primarily with data size rather than model size, a finding we justify theoretically through the analysis of infinite-width limits of neural networks and infinite-dimensional least squares regression. Of independent interest, we highlight the importance of common hyper-parameter choices and strategies for studying large-scale pre-training beyond fixed training durations.

A Study on the Calibration of In-context Learning

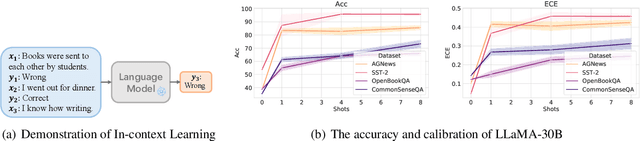
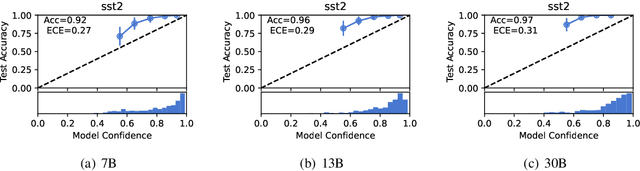
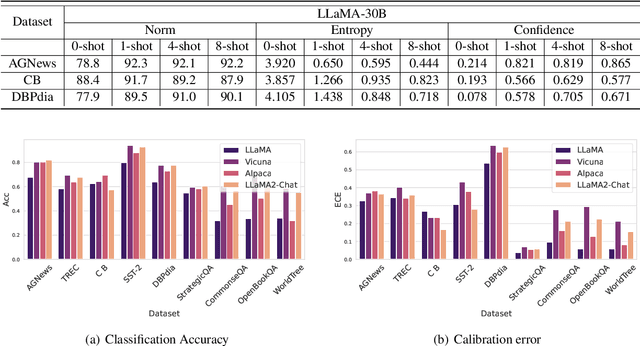
Modern auto-regressive language models are trained to minimize log loss on broad data by predicting the next token so they are expected to get calibrated answers in next-token prediction tasks. We study this for in-context learning (ICL), a widely used way to adapt frozen large language models (LLMs) via crafting prompts, and investigate the trade-offs between performance and calibration on a wide range of natural language understanding and reasoning tasks. We conduct extensive experiments to show that such trade-offs may get worse as we increase model size, incorporate more ICL examples, and fine-tune models using instruction, dialog, or reinforcement learning from human feedback (RLHF) on carefully curated datasets. Furthermore, we find that common recalibration techniques that are widely effective such as temperature scaling provide limited gains in calibration errors, suggesting that new methods may be required for settings where models are expected to be reliable.

AI safety by debate via regret minimization

We consider the setting of AI safety by debate as a repeated game. We consider the question of efficient regret minimization in this setting, when the players are either AIs or humans, equipped with access to computationally superior AIs. In such a setting, we characterize when internal and external regret can be minimized efficiently. We conclude with conditions in which a sequence of strategies converges to a correlated equilibrium.

Learning an Inventory Control Policy with General Inventory Arrival Dynamics

In this paper we address the problem of learning and backtesting inventory control policies in the presence of general arrival dynamics -- which we term as a quantity-over-time arrivals model (QOT). We also allow for order quantities to be modified as a post-processing step to meet vendor constraints such as order minimum and batch size constraints -- a common practice in real supply chains. To the best of our knowledge this is the first work to handle either arbitrary arrival dynamics or an arbitrary downstream post-processing of order quantities. Building upon recent work (Madeka et al., 2022) we similarly formulate the periodic review inventory control problem as an exogenous decision process, where most of the state is outside the control of the agent. Madeka et al. (2022) show how to construct a simulator that replays historic data to solve this class of problem. In our case, we incorporate a deep generative model for the arrivals process as part of the history replay. By formulating the problem as an exogenous decision process, we can apply results from Madeka et al. (2022) to obtain a reduction to supervised learning. Finally, we show via simulation studies that this approach yields statistically significant improvements in profitability over production baselines. Using data from an ongoing real-world A/B test, we show that Gen-QOT generalizes well to off-policy data.

Contextual Bandits for Evaluating and Improving Inventory Control Policies

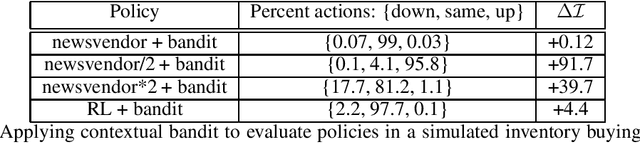
Solutions to address the periodic review inventory control problem with nonstationary random demand, lost sales, and stochastic vendor lead times typically involve making strong assumptions on the dynamics for either approximation or simulation, and applying methods such as optimization, dynamic programming, or reinforcement learning. Therefore, it is important to analyze and evaluate any inventory control policy, in particular to see if there is room for improvement. We introduce the concept of an equilibrium policy, a desirable property of a policy that intuitively means that, in hindsight, changing only a small fraction of actions does not result in materially more reward. We provide a light-weight contextual bandit-based algorithm to evaluate and occasionally tweak policies, and show that this method achieves favorable guarantees, both theoretically and in empirical studies.

Scaling Laws for Imitation Learning in NetHack

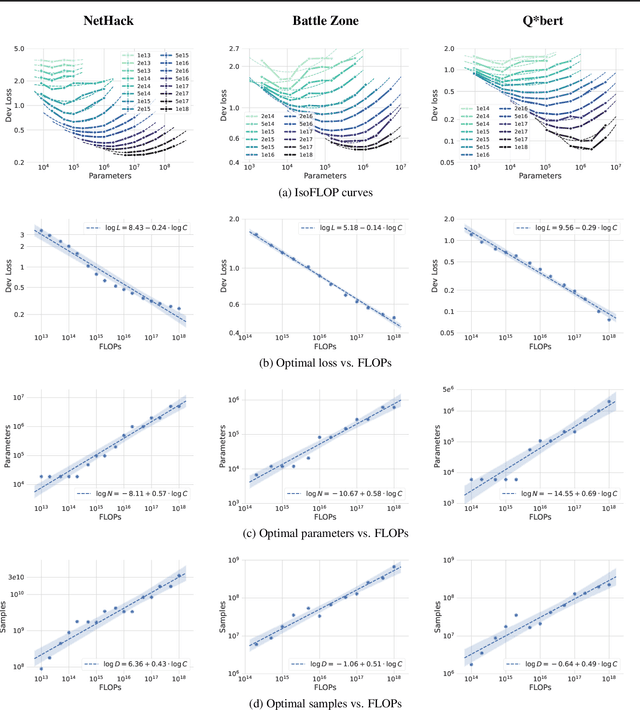
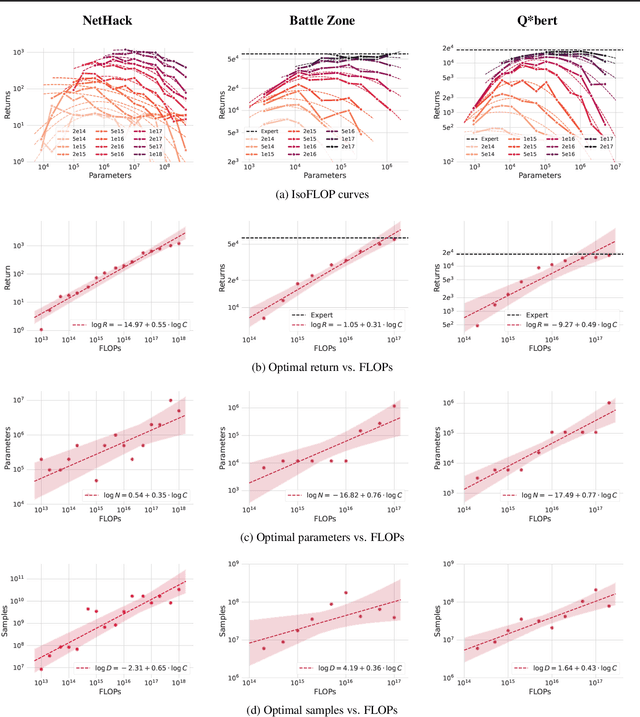
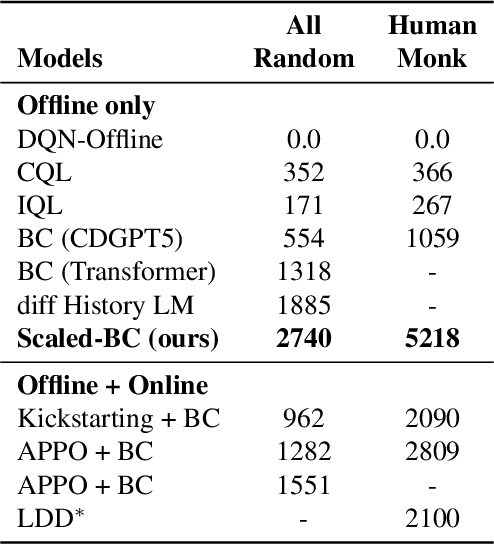
Imitation Learning (IL) is one of the most widely used methods in machine learning. Yet, while powerful, many works find it is often not able to fully recover the underlying expert behavior. However, none of these works deeply investigate the role of scaling up the model and data size. Inspired by recent work in Natural Language Processing (NLP) where "scaling up" has resulted in increasingly more capable LLMs, we investigate whether carefully scaling up model and data size can bring similar improvements in the imitation learning setting. To demonstrate our findings, we focus on the game of NetHack, a challenging environment featuring procedural generation, stochasticity, long-term dependencies, and partial observability. We find IL loss and mean return scale smoothly with the compute budget and are strongly correlated, resulting in power laws for training compute-optimal IL agents with respect to model size and number of samples. We forecast and train several NetHack agents with IL and find they outperform prior state-of-the-art by at least 2x in all settings. Our work both demonstrates the scaling behavior of imitation learning in a challenging domain, as well as the viability of scaling up current approaches for increasingly capable agents in NetHack, a game that remains elusively hard for current AI systems.

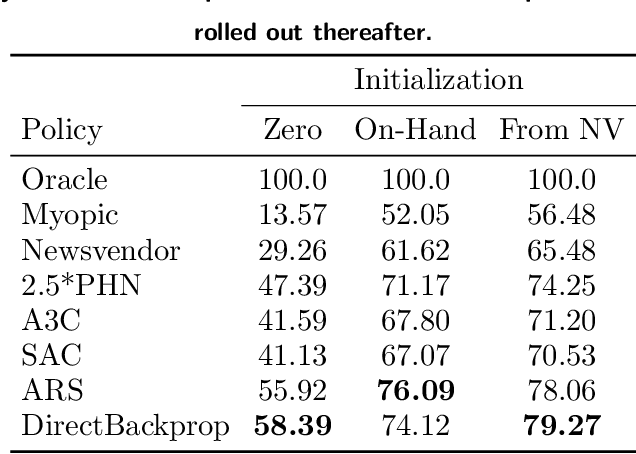
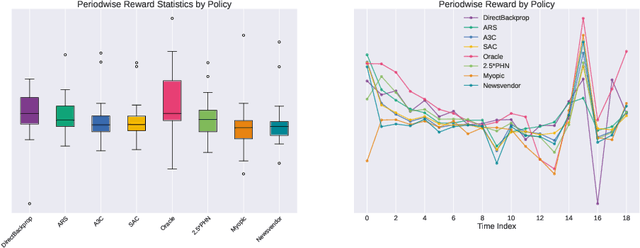
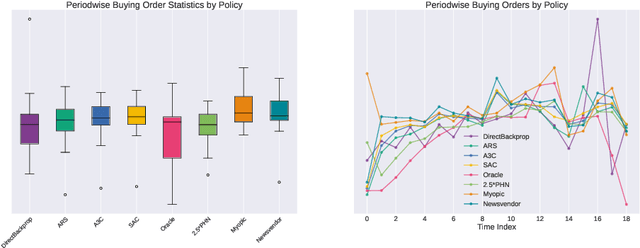
Deep Inventory Management

We present a Deep Reinforcement Learning approach to solving a periodic review inventory control system with stochastic vendor lead times, lost sales, correlated demand, and price matching. While this dynamic program has historically been considered intractable, we show that several policy learning approaches are competitive with or outperform classical baseline approaches. In order to train these algorithms, we develop novel techniques to convert historical data into a simulator. We also present a model-based reinforcement learning procedure (Direct Backprop) to solve the dynamic periodic review inventory control problem by constructing a differentiable simulator. Under a variety of metrics Direct Backprop outperforms model-free RL and newsvendor baselines, in both simulations and real-world deployments.

Assessment of Treatment Effect Estimators for Heavy-Tailed Data

A central obstacle in the objective assessment of treatment effect (TE) estimators in randomized control trials (RCTs) is the lack of ground truth (or validation set) to test their performance. In this paper, we provide a novel cross-validation-like methodology to address this challenge. The key insight of our procedure is that the noisy (but unbiased) difference-of-means estimate can be used as a ground truth "label" on a portion of the RCT, to test the performance of an estimator trained on the other portion. We combine this insight with an aggregation scheme, which borrows statistical strength across a large collection of RCTs, to present an end-to-end methodology for judging an estimator's ability to recover the underlying treatment effect. We evaluate our methodology across 709 RCTs implemented in the Amazon supply chain. In the corpus of AB tests at Amazon, we highlight the unique difficulties associated with recovering the treatment effect due to the heavy-tailed nature of the response variables. In this heavy-tailed setting, our methodology suggests that procedures that aggressively downweight or truncate large values, while introducing bias, lower the variance enough to ensure that the treatment effect is more accurately estimated.