Gemini 1.5: Unlocking multimodal understanding across millions of tokens of context

In this report, we present the latest model of the Gemini family, Gemini 1.5 Pro, a highly compute-efficient multimodal mixture-of-experts model capable of recalling and reasoning over fine-grained information from millions of tokens of context, including multiple long documents and hours of video and audio. Gemini 1.5 Pro achieves near-perfect recall on long-context retrieval tasks across modalities, improves the state-of-the-art in long-document QA, long-video QA and long-context ASR, and matches or surpasses Gemini 1.0 Ultra's state-of-the-art performance across a broad set of benchmarks. Studying the limits of Gemini 1.5 Pro's long-context ability, we find continued improvement in next-token prediction and near-perfect retrieval (>99%) up to at least 10M tokens, a generational leap over existing models such as Claude 2.1 (200k) and GPT-4 Turbo (128k). Finally, we highlight surprising new capabilities of large language models at the frontier; when given a grammar manual for Kalamang, a language with fewer than 200 speakers worldwide, the model learns to translate English to Kalamang at a similar level to a person who learned from the same content.

Gemini: A Family of Highly Capable Multimodal Models

This report introduces a new family of multimodal models, Gemini, that exhibit remarkable capabilities across image, audio, video, and text understanding. The Gemini family consists of Ultra, Pro, and Nano sizes, suitable for applications ranging from complex reasoning tasks to on-device memory-constrained use-cases. Evaluation on a broad range of benchmarks shows that our most-capable Gemini Ultra model advances the state of the art in 30 of 32 of these benchmarks - notably being the first model to achieve human-expert performance on the well-studied exam benchmark MMLU, and improving the state of the art in every one of the 20 multimodal benchmarks we examined. We believe that the new capabilities of Gemini models in cross-modal reasoning and language understanding will enable a wide variety of use cases and we discuss our approach toward deploying them responsibly to users.

Pretraining Data Mixtures Enable Narrow Model Selection Capabilities in Transformer Models

Transformer models, notably large language models (LLMs), have the remarkable ability to perform in-context learning (ICL) -- to perform new tasks when prompted with unseen input-output examples without any explicit model training. In this work, we study how effectively transformers can bridge between their pretraining data mixture, comprised of multiple distinct task families, to identify and learn new tasks in-context which are both inside and outside the pretraining distribution. Building on previous work, we investigate this question in a controlled setting, where we study transformer models trained on sequences of $(x, f(x))$ pairs rather than natural language. Our empirical results show transformers demonstrate near-optimal unsupervised model selection capabilities, in their ability to first in-context identify different task families and in-context learn within them when the task families are well-represented in their pretraining data. However when presented with tasks or functions which are out-of-domain of their pretraining data, we demonstrate various failure modes of transformers and degradation of their generalization for even simple extrapolation tasks. Together our results highlight that the impressive ICL abilities of high-capacity sequence models may be more closely tied to the coverage of their pretraining data mixtures than inductive biases that create fundamental generalization capabilities.

Choosing a Proxy Metric from Past Experiments

In many randomized experiments, the treatment effect of the long-term metric (i.e. the primary outcome of interest) is often difficult or infeasible to measure. Such long-term metrics are often slow to react to changes and sufficiently noisy they are challenging to faithfully estimate in short-horizon experiments. A common alternative is to measure several short-term proxy metrics in the hope they closely track the long-term metric -- so they can be used to effectively guide decision-making in the near-term. We introduce a new statistical framework to both define and construct an optimal proxy metric for use in a homogeneous population of randomized experiments. Our procedure first reduces the construction of an optimal proxy metric in a given experiment to a portfolio optimization problem which depends on the true latent treatment effects and noise level of experiment under consideration. We then denoise the observed treatment effects of the long-term metric and a set of proxies in a historical corpus of randomized experiments to extract estimates of the latent treatment effects for use in the optimization problem. One key insight derived from our approach is that the optimal proxy metric for a given experiment is not apriori fixed; rather it should depend on the sample size (or effective noise level) of the randomized experiment for which it is deployed. To instantiate and evaluate our framework, we employ our methodology in a large corpus of randomized experiments from an industrial recommendation system and construct proxy metrics that perform favorably relative to several baselines.

Assessment of Treatment Effect Estimators for Heavy-Tailed Data

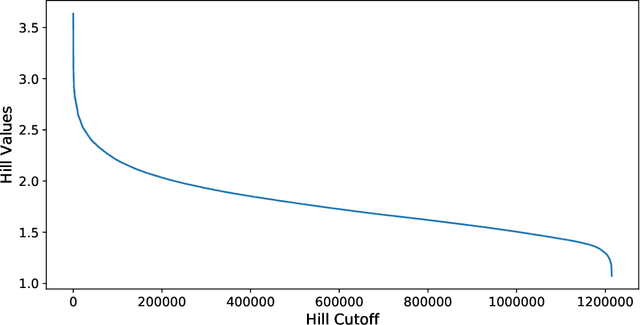
A central obstacle in the objective assessment of treatment effect (TE) estimators in randomized control trials (RCTs) is the lack of ground truth (or validation set) to test their performance. In this paper, we provide a novel cross-validation-like methodology to address this challenge. The key insight of our procedure is that the noisy (but unbiased) difference-of-means estimate can be used as a ground truth "label" on a portion of the RCT, to test the performance of an estimator trained on the other portion. We combine this insight with an aggregation scheme, which borrows statistical strength across a large collection of RCTs, to present an end-to-end methodology for judging an estimator's ability to recover the underlying treatment effect. We evaluate our methodology across 709 RCTs implemented in the Amazon supply chain. In the corpus of AB tests at Amazon, we highlight the unique difficulties associated with recovering the treatment effect due to the heavy-tailed nature of the response variables. In this heavy-tailed setting, our methodology suggests that procedures that aggressively downweight or truncate large values, while introducing bias, lower the variance enough to ensure that the treatment effect is more accurately estimated.

Covariate Shift in High-Dimensional Random Feature Regression

A significant obstacle in the development of robust machine learning models is covariate shift, a form of distribution shift that occurs when the input distributions of the training and test sets differ while the conditional label distributions remain the same. Despite the prevalence of covariate shift in real-world applications, a theoretical understanding in the context of modern machine learning has remained lacking. In this work, we examine the exact high-dimensional asymptotics of random feature regression under covariate shift and present a precise characterization of the limiting test error, bias, and variance in this setting. Our results motivate a natural partial order over covariate shifts that provides a sufficient condition for determining when the shift will harm (or even help) test performance. We find that overparameterized models exhibit enhanced robustness to covariate shift, providing one of the first theoretical explanations for this intriguing phenomenon. Additionally, our analysis reveals an exact linear relationship between in-distribution and out-of-distribution generalization performance, offering an explanation for this surprising recent empirical observation.

Parallelizing Contextual Linear Bandits

Standard approaches to decision-making under uncertainty focus on sequential exploration of the space of decisions. However, \textit{simultaneously} proposing a batch of decisions, which leverages available resources for parallel experimentation, has the potential to rapidly accelerate exploration. We present a family of (parallel) contextual linear bandit algorithms, whose regret is nearly identical to their perfectly sequential counterparts -- given access to the same total number of oracle queries -- up to a lower-order "burn-in" term that is dependent on the context-set geometry. We provide matching information-theoretic lower bounds on parallel regret performance to establish our algorithms are asymptotically optimal in the time horizon. Finally, we also present an empirical evaluation of these parallel algorithms in several domains, including materials discovery and biological sequence design problems, to demonstrate the utility of parallelized bandits in practical settings.

Optimal Mean Estimation without a Variance

We study the problem of heavy-tailed mean estimation in settings where the variance of the data-generating distribution does not exist. Concretely, given a sample $\mathbf{X} = \{X_i\}_{i = 1}^n$ from a distribution $\mathcal{D}$ over $\mathbb{R}^d$ with mean $\mu$ which satisfies the following \emph{weak-moment} assumption for some ${\alpha \in [0, 1]}$: \begin{equation*} \forall \|v\| = 1: \mathbb{E}_{X \thicksim \mathcal{D}}[\lvert \langle X - \mu, v\rangle \rvert^{1 + \alpha}] \leq 1, \end{equation*} and given a target failure probability, $\delta$, our goal is to design an estimator which attains the smallest possible confidence interval as a function of $n,d,\delta$. For the specific case of $\alpha = 1$, foundational work of Lugosi and Mendelson exhibits an estimator achieving subgaussian confidence intervals, and subsequent work has led to computationally efficient versions of this estimator. Here, we study the case of general $\alpha$, and establish the following information-theoretic lower bound on the optimal attainable confidence interval: \begin{equation*} \Omega \left(\sqrt{\frac{d}{n}} + \left(\frac{d}{n}\right)^{\frac{\alpha}{(1 + \alpha)}} + \left(\frac{\log 1 / \delta}{n}\right)^{\frac{\alpha}{(1 + \alpha)}}\right). \end{equation*} Moreover, we devise a computationally-efficient estimator which achieves this lower bound.

Optimal Robust Linear Regression in Nearly Linear Time

We study the problem of high-dimensional robust linear regression where a learner is given access to $n$ samples from the generative model $Y = \langle X,w^* \rangle + \epsilon$ (with $X \in \mathbb{R}^d$ and $\epsilon$ independent), in which an $\eta$ fraction of the samples have been adversarially corrupted. We propose estimators for this problem under two settings: (i) $X$ is L4-L2 hypercontractive, $\mathbb{E} [XX^\top]$ has bounded condition number and $\epsilon$ has bounded variance and (ii) $X$ is sub-Gaussian with identity second moment and $\epsilon$ is sub-Gaussian. In both settings, our estimators: (a) Achieve optimal sample complexities and recovery guarantees up to log factors and (b) Run in near linear time ($\tilde{O}(nd / \eta^6)$). Prior to our work, polynomial time algorithms achieving near optimal sample complexities were only known in the setting where $X$ is Gaussian with identity covariance and $\epsilon$ is Gaussian, and no linear time estimators were known for robust linear regression in any setting. Our estimators and their analysis leverage recent developments in the construction of faster algorithms for robust mean estimation to improve runtimes, and refined concentration of measure arguments alongside Gaussian rounding techniques to improve statistical sample complexities.

On the Theory of Transfer Learning: The Importance of Task Diversity

We provide new statistical guarantees for transfer learning via representation learning--when transfer is achieved by learning a feature representation shared across different tasks. This enables learning on new tasks using far less data than is required to learn them in isolation. Formally, we consider $t+1$ tasks parameterized by functions of the form $f_j \circ h$ in a general function class $\mathcal{F} \circ \mathcal{H}$, where each $f_j$ is a task-specific function in $\mathcal{F}$ and $h$ is the shared representation in $\mathcal{H}$. Letting $C(\cdot)$ denote the complexity measure of the function class, we show that for diverse training tasks (1) the sample complexity needed to learn the shared representation across the first $t$ training tasks scales as $C(\mathcal{H}) + t C(\mathcal{F})$, despite no explicit access to a signal from the feature representation and (2) with an accurate estimate of the representation, the sample complexity needed to learn a new task scales only with $C(\mathcal{F})$. Our results depend upon a new general notion of task diversity--applicable to models with general tasks, features, and losses--as well as a novel chain rule for Gaussian complexities. Finally, we exhibit the utility of our general framework in several models of importance in the literature.