Training Language Models on the Knowledge Graph: Insights on Hallucinations and Their Detectability

While many capabilities of language models (LMs) improve with increased training budget, the influence of scale on hallucinations is not yet fully understood. Hallucinations come in many forms, and there is no universally accepted definition. We thus focus on studying only those hallucinations where a correct answer appears verbatim in the training set. To fully control the training data content, we construct a knowledge graph (KG)-based dataset, and use it to train a set of increasingly large LMs. We find that for a fixed dataset, larger and longer-trained LMs hallucinate less. However, hallucinating on $\leq5$% of the training data requires an order of magnitude larger model, and thus an order of magnitude more compute, than Hoffmann et al. (2022) reported was optimal. Given this costliness, we study how hallucination detectors depend on scale. While we see detector size improves performance on fixed LM's outputs, we find an inverse relationship between the scale of the LM and the detectability of its hallucinations.

Scaling Exponents Across Parameterizations and Optimizers

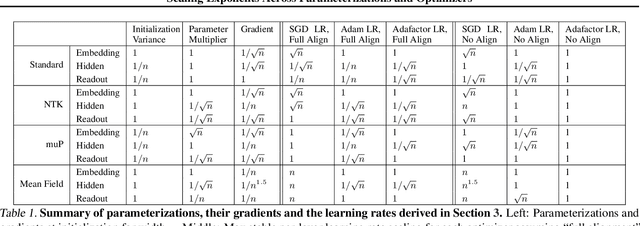
Robust and effective scaling of models from small to large width typically requires the precise adjustment of many algorithmic and architectural details, such as parameterization and optimizer choices. In this work, we propose a new perspective on parameterization by investigating a key assumption in prior work about the alignment between parameters and data and derive new theoretical results under weaker assumptions and a broader set of optimizers. Our extensive empirical investigation includes tens of thousands of models trained with all combinations of three optimizers, four parameterizations, several alignment assumptions, more than a dozen learning rates, and fourteen model sizes up to 26.8B parameters. We find that the best learning rate scaling prescription would often have been excluded by the assumptions in prior work. Our results show that all parameterizations, not just maximal update parameterization (muP), can achieve hyperparameter transfer; moreover, our novel per-layer learning rate prescription for standard parameterization outperforms muP. Finally, we demonstrate that an overlooked aspect of parameterization, the epsilon parameter in Adam, must be scaled correctly to avoid gradient underflow and propose Adam-atan2, a new numerically stable, scale-invariant version of Adam that eliminates the epsilon hyperparameter entirely.

4+3 Phases of Compute-Optimal Neural Scaling Laws

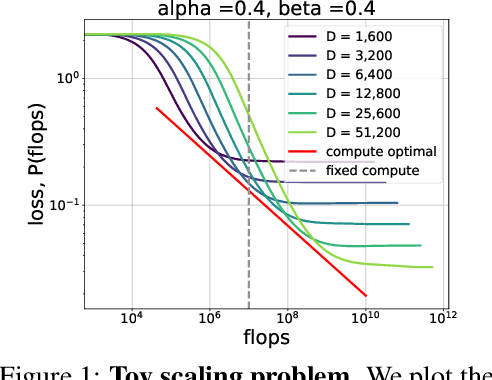
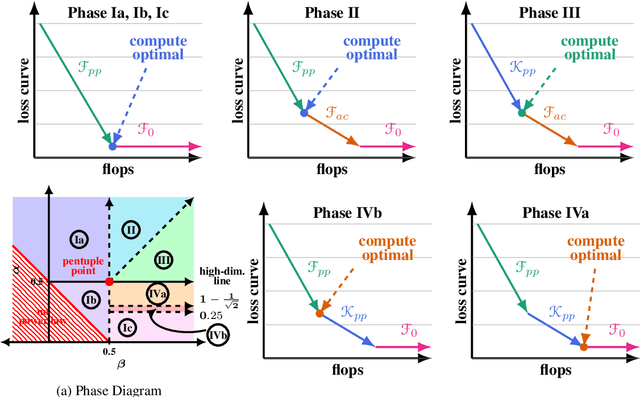
We consider the three parameter solvable neural scaling model introduced by Maloney, Roberts, and Sully. The model has three parameters: data complexity, target complexity, and model-parameter-count. We use this neural scaling model to derive new predictions about the compute-limited, infinite-data scaling law regime. To train the neural scaling model, we run one-pass stochastic gradient descent on a mean-squared loss. We derive a representation of the loss curves which holds over all iteration counts and improves in accuracy as the model parameter count grows. We then analyze the compute-optimal model-parameter-count, and identify 4 phases (+3 subphases) in the data-complexity/target-complexity phase-plane. The phase boundaries are determined by the relative importance of model capacity, optimizer noise, and embedding of the features. We furthermore derive, with mathematical proof and extensive numerical evidence, the scaling-law exponents in all of these phases, in particular computing the optimal model-parameter-count as a function of floating point operation budget.

High dimensional analysis reveals conservative sharpening and a stochastic edge of stability

Recent empirical and theoretical work has shown that the dynamics of the large eigenvalues of the training loss Hessian have some remarkably robust features across models and datasets in the full batch regime. There is often an early period of progressive sharpening where the large eigenvalues increase, followed by stabilization at a predictable value known as the edge of stability. Previous work showed that in the stochastic setting, the eigenvalues increase more slowly - a phenomenon we call conservative sharpening. We provide a theoretical analysis of a simple high-dimensional model which shows the origin of this slowdown. We also show that there is an alternative stochastic edge of stability which arises at small batch size that is sensitive to the trace of the Neural Tangent Kernel rather than the large Hessian eigenvalues. We conduct an experimental study which highlights the qualitative differences from the full batch phenomenology, and suggests that controlling the stochastic edge of stability can help optimization.

Training LLMs over Neurally Compressed Text

In this paper, we explore the idea of training large language models (LLMs) over highly compressed text. While standard subword tokenizers compress text by a small factor, neural text compressors can achieve much higher rates of compression. If it were possible to train LLMs directly over neurally compressed text, this would confer advantages in training and serving efficiency, as well as easier handling of long text spans. The main obstacle to this goal is that strong compression tends to produce opaque outputs that are not well-suited for learning. In particular, we find that text na\"ively compressed via Arithmetic Coding is not readily learnable by LLMs. To overcome this, we propose Equal-Info Windows, a novel compression technique whereby text is segmented into blocks that each compress to the same bit length. Using this method, we demonstrate effective learning over neurally compressed text that improves with scale, and outperforms byte-level baselines by a wide margin on perplexity and inference speed benchmarks. While our method delivers worse perplexity than subword tokenizers for models trained with the same parameter count, it has the benefit of shorter sequence lengths. Shorter sequence lengths require fewer autoregressive generation steps, and reduce latency. Finally, we provide extensive analysis of the properties that contribute to learnability, and offer concrete suggestions for how to further improve the performance of high-compression tokenizers.

Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

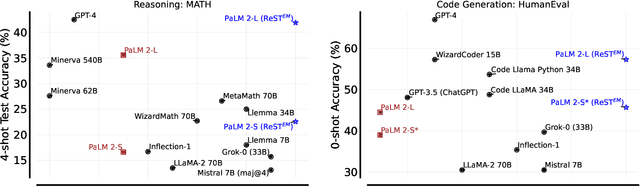
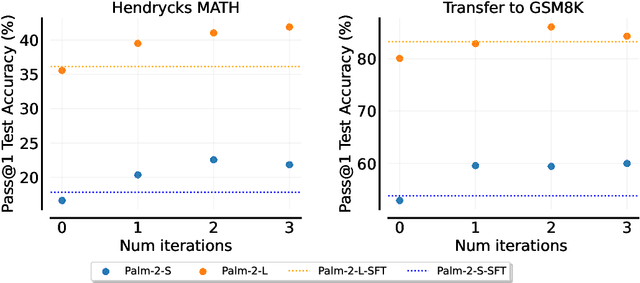
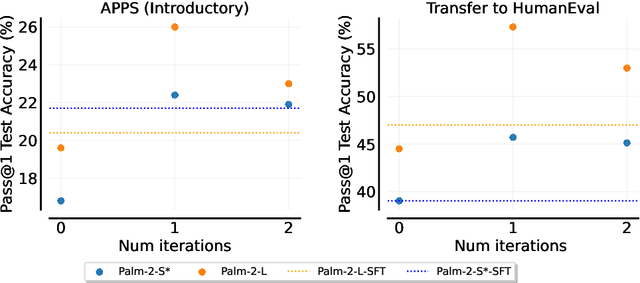
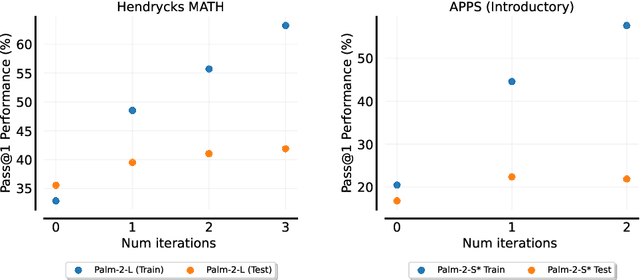
Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.

Frontier Language Models are not Robust to Adversarial Arithmetic, or "What do I need to say so you agree 2+2=5?

We introduce and study the problem of adversarial arithmetic, which provides a simple yet challenging testbed for language model alignment. This problem is comprised of arithmetic questions posed in natural language, with an arbitrary adversarial string inserted before the question is complete. Even in the simple setting of 1-digit addition problems, it is easy to find adversarial prompts that make all tested models (including PaLM2, GPT4, Claude2) misbehave, and even to steer models to a particular wrong answer. We additionally provide a simple algorithm for finding successful attacks by querying those same models, which we name "prompt inversion rejection sampling" (PIRS). We finally show that models can be partially hardened against these attacks via reinforcement learning and via agentic constitutional loops. However, we were not able to make a language model fully robust against adversarial arithmetic attacks.

Small-scale proxies for large-scale Transformer training instabilities

Teams that have trained large Transformer-based models have reported training instabilities at large scale that did not appear when training with the same hyperparameters at smaller scales. Although the causes of such instabilities are of scientific interest, the amount of resources required to reproduce them has made investigation difficult. In this work, we seek ways to reproduce and study training stability and instability at smaller scales. First, we focus on two sources of training instability described in previous work: the growth of logits in attention layers (Dehghani et al., 2023) and divergence of the output logits from the log probabilities (Chowdhery et al., 2022). By measuring the relationship between learning rate and loss across scales, we show that these instabilities also appear in small models when training at high learning rates, and that mitigations previously employed at large scales are equally effective in this regime. This prompts us to investigate the extent to which other known optimizer and model interventions influence the sensitivity of the final loss to changes in the learning rate. To this end, we study methods such as warm-up, weight decay, and the $\mu$Param (Yang et al., 2022), and combine techniques to train small models that achieve similar losses across orders of magnitude of learning rate variation. Finally, to conclude our exploration we study two cases where instabilities can be predicted before they emerge by examining the scaling behavior of model activation and gradient norms.

Second-order regression models exhibit progressive sharpening to the edge of stability

Recent studies of gradient descent with large step sizes have shown that there is often a regime with an initial increase in the largest eigenvalue of the loss Hessian (progressive sharpening), followed by a stabilization of the eigenvalue near the maximum value which allows convergence (edge of stability). These phenomena are intrinsically non-linear and do not happen for models in the constant Neural Tangent Kernel (NTK) regime, for which the predictive function is approximately linear in the parameters. As such, we consider the next simplest class of predictive models, namely those that are quadratic in the parameters, which we call second-order regression models. For quadratic objectives in two dimensions, we prove that this second-order regression model exhibits progressive sharpening of the NTK eigenvalue towards a value that differs slightly from the edge of stability, which we explicitly compute. In higher dimensions, the model generically shows similar behavior, even without the specific structure of a neural network, suggesting that progressive sharpening and edge-of-stability behavior aren't unique features of neural networks, and could be a more general property of discrete learning algorithms in high-dimensional non-linear models.

Synergy and Symmetry in Deep Learning: Interactions between the Data, Model, and Inference Algorithm

Although learning in high dimensions is commonly believed to suffer from the curse of dimensionality, modern machine learning methods often exhibit an astonishing power to tackle a wide range of challenging real-world learning problems without using abundant amounts of data. How exactly these methods break this curse remains a fundamental open question in the theory of deep learning. While previous efforts have investigated this question by studying the data (D), model (M), and inference algorithm (I) as independent modules, in this paper, we analyze the triplet (D, M, I) as an integrated system and identify important synergies that help mitigate the curse of dimensionality. We first study the basic symmetries associated with various learning algorithms (M, I), focusing on four prototypical architectures in deep learning: fully-connected networks (FCN), locally-connected networks (LCN), and convolutional networks with and without pooling (GAP/VEC). We find that learning is most efficient when these symmetries are compatible with those of the data distribution and that performance significantly deteriorates when any member of the (D, M, I) triplet is inconsistent or suboptimal.