Reproducibility in the Control of Autonomous Mobility-on-Demand Systems

Autonomous Mobility-on-Demand (AMoD) systems, powered by advances in robotics, control, and Machine Learning (ML), offer a promising paradigm for future urban transportation. AMoD offers fast and personalized travel services by leveraging centralized control of autonomous vehicle fleets to optimize operations and enhance service performance. However, the rapid growth of this field has outpaced the development of standardized practices for evaluating and reporting results, leading to significant challenges in reproducibility. As AMoD control algorithms become increasingly complex and data-driven, a lack of transparency in modeling assumptions, experimental setups, and algorithmic implementation hinders scientific progress and undermines confidence in the results. This paper presents a systematic study of reproducibility in AMoD research. We identify key components across the research pipeline, spanning system modeling, control problems, simulation design, algorithm specification, and evaluation, and analyze common sources of irreproducibility. We survey prevalent practices in the literature, highlight gaps, and propose a structured framework to assess and improve reproducibility. Specifically, concrete guidelines are offered, along with a "reproducibility checklist", to support future work in achieving replicable, comparable, and extensible results. While focused on AMoD, the principles and practices we advocate generalize to a broader class of cyber-physical systems that rely on networked autonomy and data-driven control. This work aims to lay the foundation for a more transparent and reproducible research culture in the design and deployment of intelligent mobility systems.

Robo-taxi Fleet Coordination at Scale via Reinforcement Learning

Fleets of robo-taxis offering on-demand transportation services, commonly known as Autonomous Mobility-on-Demand (AMoD) systems, hold significant promise for societal benefits, such as reducing pollution, energy consumption, and urban congestion. However, orchestrating these systems at scale remains a critical challenge, with existing coordination algorithms often failing to exploit the systems' full potential. This work introduces a novel decision-making framework that unites mathematical modeling with data-driven techniques. In particular, we present the AMoD coordination problem through the lens of reinforcement learning and propose a graph network-based framework that exploits the main strengths of graph representation learning, reinforcement learning, and classical operations research tools. Extensive evaluations across diverse simulation fidelities and scenarios demonstrate the flexibility of our approach, achieving superior system performance, computational efficiency, and generalizability compared to prior methods. Finally, motivated by the need to democratize research efforts in this area, we release publicly available benchmarks, datasets, and simulators for network-level coordination alongside an open-source codebase designed to provide accessible simulation platforms and establish a standardized validation process for comparing methodologies. Code available at: https://github.com/StanfordASL/RL4AMOD

Bayesian Optimization via Continual Variational Last Layer Training

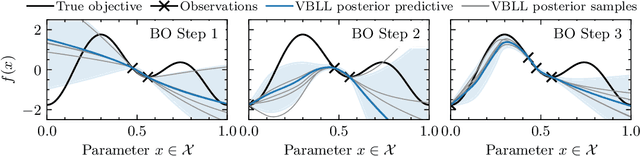
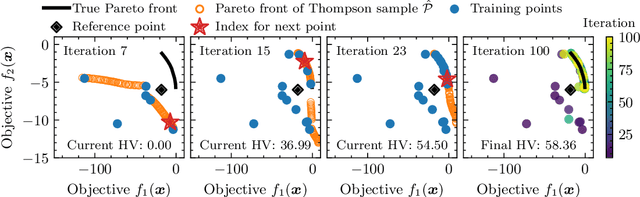
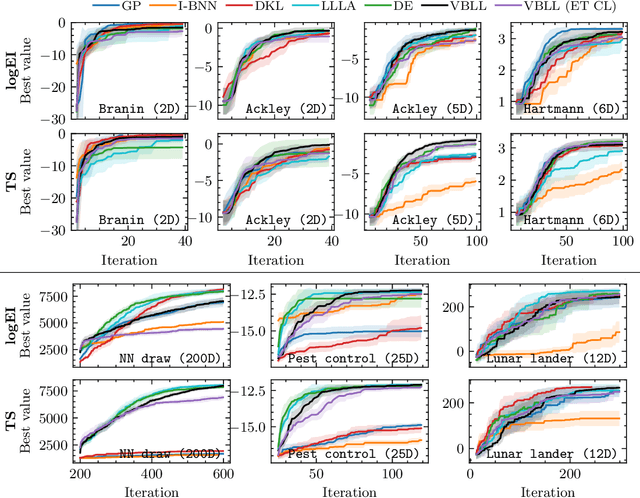
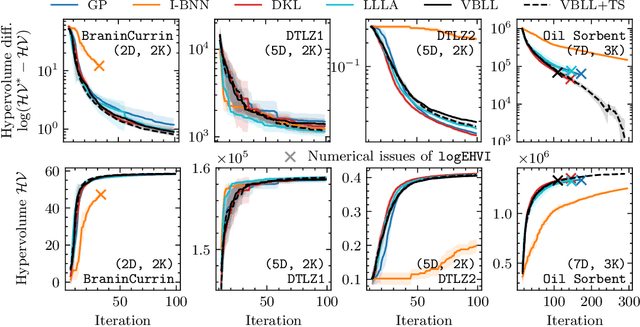
Gaussian Processes (GPs) are widely seen as the state-of-the-art surrogate models for Bayesian optimization (BO) due to their ability to model uncertainty and their performance on tasks where correlations are easily captured (such as those defined by Euclidean metrics) and their ability to be efficiently updated online. However, the performance of GPs depends on the choice of kernel, and kernel selection for complex correlation structures is often difficult or must be made bespoke. While Bayesian neural networks (BNNs) are a promising direction for higher capacity surrogate models, they have so far seen limited use due to poor performance on some problem types. In this paper, we propose an approach which shows competitive performance on many problem types, including some that BNNs typically struggle with. We build on variational Bayesian last layers (VBLLs), and connect training of these models to exact conditioning in GPs. We exploit this connection to develop an efficient online training algorithm that interleaves conditioning and optimization. Our findings suggest that VBLL networks significantly outperform GPs and other BNN architectures on tasks with complex input correlations, and match the performance of well-tuned GPs on established benchmark tasks.

Applications of fractional calculus in learned optimization

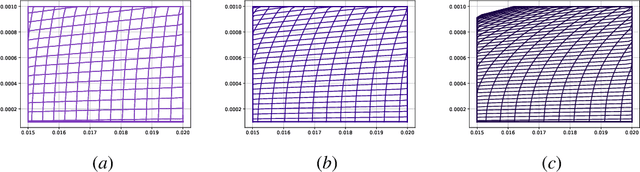
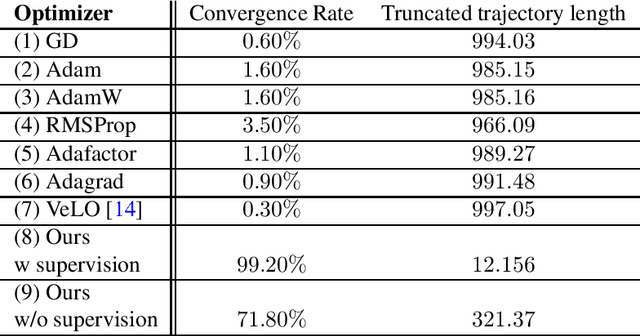
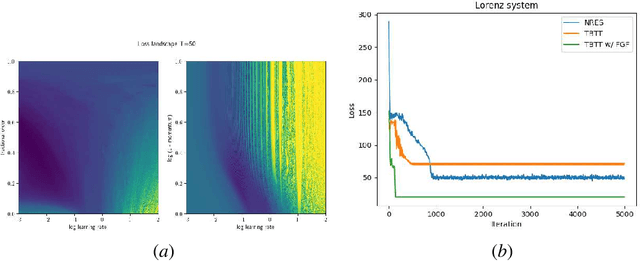
Fractional gradient descent has been studied extensively, with a focus on its ability to extend traditional gradient descent methods by incorporating fractional-order derivatives. This approach allows for more flexibility in navigating complex optimization landscapes and offers advantages in certain types of problems, particularly those involving non-linearities and chaotic dynamics. Yet, the challenge of fine-tuning the fractional order parameters remains unsolved. In this work, we demonstrate that it is possible to train a neural network to predict the order of the gradient effectively.

Offline Hierarchical Reinforcement Learning via Inverse Optimization

Hierarchical policies enable strong performance in many sequential decision-making problems, such as those with high-dimensional action spaces, those requiring long-horizon planning, and settings with sparse rewards. However, learning hierarchical policies from static offline datasets presents a significant challenge. Crucially, actions taken by higher-level policies may not be directly observable within hierarchical controllers, and the offline dataset might have been generated using a different policy structure, hindering the use of standard offline learning algorithms. In this work, we propose OHIO: a framework for offline reinforcement learning (RL) of hierarchical policies. Our framework leverages knowledge of the policy structure to solve the inverse problem, recovering the unobservable high-level actions that likely generated the observed data under our hierarchical policy. This approach constructs a dataset suitable for off-the-shelf offline training. We demonstrate our framework on robotic and network optimization problems and show that it substantially outperforms end-to-end RL methods and improves robustness. We investigate a variety of instantiations of our framework, both in direct deployment of policies trained offline and when online fine-tuning is performed.

Long-Horizon Planning for Multi-Agent Robots in Partially Observable Environments

The ability of Language Models (LMs) to understand natural language makes them a powerful tool for parsing human instructions into task plans for autonomous robots. Unlike traditional planning methods that rely on domain-specific knowledge and handcrafted rules, LMs generalize from diverse data and adapt to various tasks with minimal tuning, acting as a compressed knowledge base. However, LMs in their standard form face challenges with long-horizon tasks, particularly in partially observable multi-agent settings. We propose an LM-based Long-Horizon Planner for Multi-Agent Robotics (LLaMAR), a cognitive architecture for planning that achieves state-of-the-art results in long-horizon tasks within partially observable environments. LLaMAR employs a plan-act-correct-verify framework, allowing self-correction from action execution feedback without relying on oracles or simulators. Additionally, we present MAP-THOR, a comprehensive test suite encompassing household tasks of varying complexity within the AI2-THOR environment. Experiments show that LLaMAR achieves a 30% higher success rate compared to other state-of-the-art LM-based multi-agent planners.

Variational Bayesian Last Layers

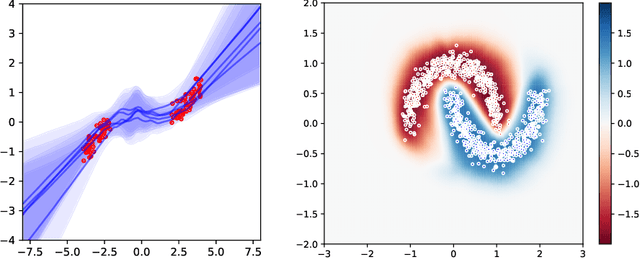
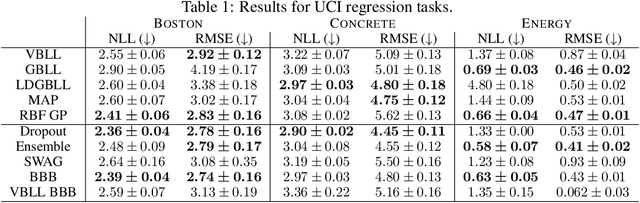
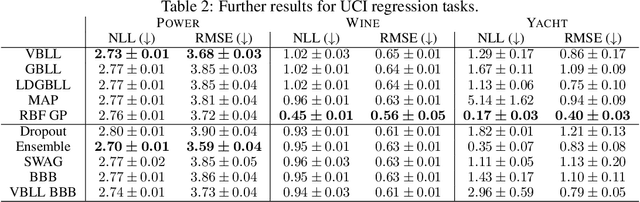
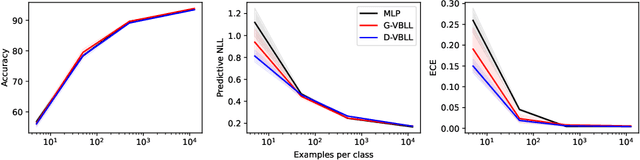
We introduce a deterministic variational formulation for training Bayesian last layer neural networks. This yields a sampling-free, single-pass model and loss that effectively improves uncertainty estimation. Our variational Bayesian last layer (VBLL) can be trained and evaluated with only quadratic complexity in last layer width, and is thus (nearly) computationally free to add to standard architectures. We experimentally investigate VBLLs, and show that they improve predictive accuracy, calibration, and out of distribution detection over baselines across both regression and classification. Finally, we investigate combining VBLL layers with variational Bayesian feature learning, yielding a lower variance collapsed variational inference method for Bayesian neural networks.

Risk-Sensitive Soft Actor-Critic for Robust Deep Reinforcement Learning under Distribution Shifts

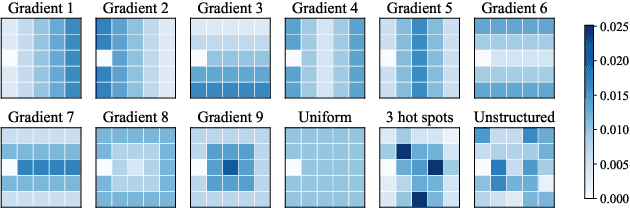
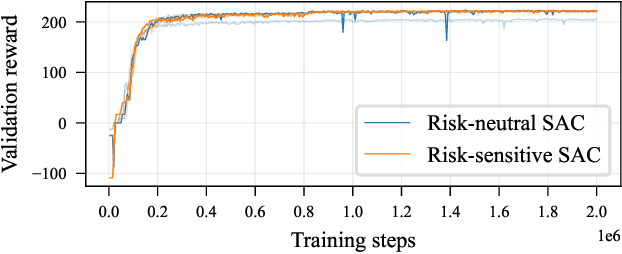
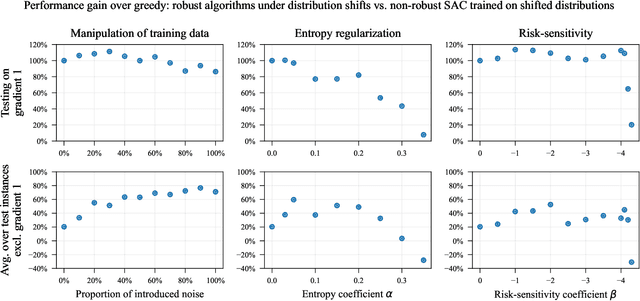
We study the robustness of deep reinforcement learning algorithms against distribution shifts within contextual multi-stage stochastic combinatorial optimization problems from the operations research domain. In this context, risk-sensitive algorithms promise to learn robust policies. While this field is of general interest to the reinforcement learning community, most studies up-to-date focus on theoretical results rather than real-world performance. With this work, we aim to bridge this gap by formally deriving a novel risk-sensitive deep reinforcement learning algorithm while providing numerical evidence for its efficacy. Specifically, we introduce discrete Soft Actor-Critic for the entropic risk measure by deriving a version of the Bellman equation for the respective Q-values. We establish a corresponding policy improvement result and infer a practical algorithm. We introduce an environment that represents typical contextual multi-stage stochastic combinatorial optimization problems and perform numerical experiments to empirically validate our algorithm's robustness against realistic distribution shifts, without compromising performance on the training distribution. We show that our algorithm is superior to risk-neutral Soft Actor-Critic as well as to two benchmark approaches for robust deep reinforcement learning. Thereby, we provide the first structured analysis on the robustness of reinforcement learning under distribution shifts in the realm of contextual multi-stage stochastic combinatorial optimization problems.

Universal Neural Functionals

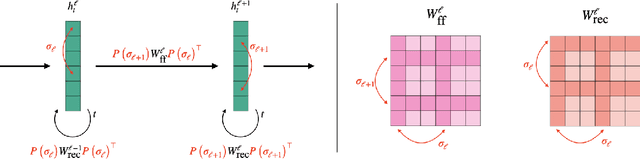
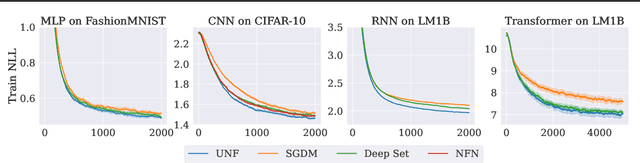
A challenging problem in many modern machine learning tasks is to process weight-space features, i.e., to transform or extract information from the weights and gradients of a neural network. Recent works have developed promising weight-space models that are equivariant to the permutation symmetries of simple feedforward networks. However, they are not applicable to general architectures, since the permutation symmetries of a weight space can be complicated by recurrence or residual connections. This work proposes an algorithm that automatically constructs permutation equivariant models, which we refer to as universal neural functionals (UNFs), for any weight space. Among other applications, we demonstrate how UNFs can be substituted into existing learned optimizer designs, and find promising improvements over prior methods when optimizing small image classifiers and language models. Our results suggest that learned optimizers can benefit from considering the (symmetry) structure of the weight space they optimize. We open-source our library for constructing UNFs at https://github.com/AllanYangZhou/universal_neural_functional.

Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

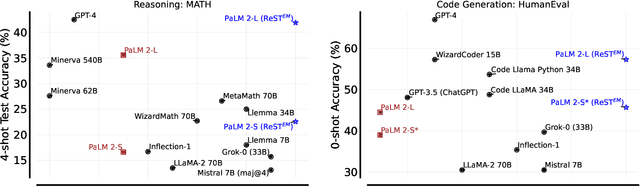
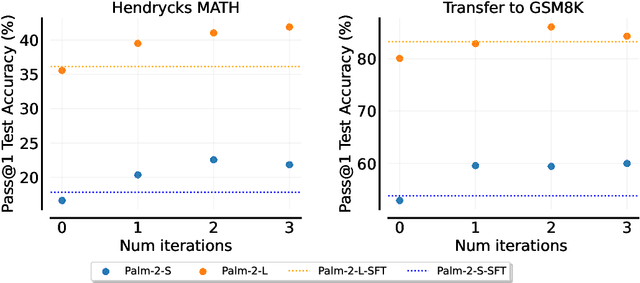
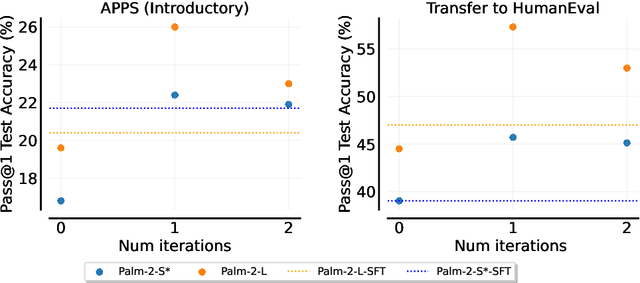
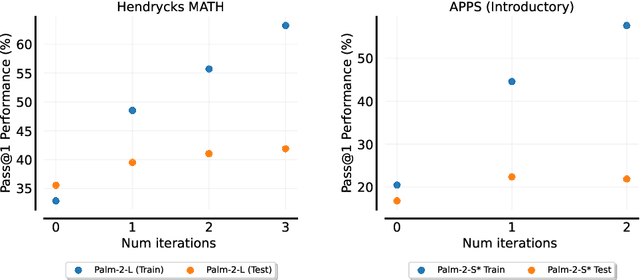
Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.