BayeSQP: Bayesian Optimization through Sequential Quadratic Programming

We introduce BayeSQP, a novel algorithm for general black-box optimization that merges the structure of sequential quadratic programming with concepts from Bayesian optimization. BayeSQP employs second-order Gaussian process surrogates for both the objective and constraints to jointly model the function values, gradients, and Hessian from only zero-order information. At each iteration, a local subproblem is constructed using the GP posterior estimates and solved to obtain a search direction. Crucially, the formulation of the subproblem explicitly incorporates uncertainty in both the function and derivative estimates, resulting in a tractable second-order cone program for high probability improvements under model uncertainty. A subsequent one-dimensional line search via constrained Thompson sampling selects the next evaluation point. Empirical results show thatBayeSQP outperforms state-of-the-art methods in specific high-dimensional settings. Our algorithm offers a principled and flexible framework that bridges classical optimization techniques with modern approaches to black-box optimization.

Vision-Conditioned Variational Bayesian Last Layer Dynamics Models

Agile control of robotic systems often requires anticipating how the environment affects system behavior. For example, a driver must perceive the road ahead to anticipate available friction and plan actions accordingly. Achieving such proactive adaptation within autonomous frameworks remains a challenge, particularly under rapidly changing conditions. Traditional modeling approaches often struggle to capture abrupt variations in system behavior, while adaptive methods are inherently reactive and may adapt too late to ensure safety. We propose a vision-conditioned variational Bayesian last-layer dynamics model that leverages visual context to anticipate changes in the environment. The model first learns nominal vehicle dynamics and is then fine-tuned with feature-wise affine transformations of latent features, enabling context-aware dynamics prediction. The resulting model is integrated into an optimal controller for vehicle racing. We validate our method on a Lexus LC500 racing through water puddles. With vision-conditioning, the system completed all 12 attempted laps under varying conditions. In contrast, all baselines without visual context consistently lost control, demonstrating the importance of proactive dynamics adaptation in high-performance applications.

The Mini Wheelbot Dataset: High-Fidelity Data for Robot Learning

The development of robust learning-based control algorithms for unstable systems requires high-quality, real-world data, yet access to specialized robotic hardware remains a significant barrier for many researchers. This paper introduces a comprehensive dynamics dataset for the Mini Wheelbot, an open-source, quasi-symmetric balancing reaction wheel unicycle. The dataset provides 1 kHz synchronized data encompassing all onboard sensor readings, state estimates, ground-truth poses from a motion capture system, and third-person video logs. To ensure data diversity, we include experiments across multiple hardware instances and surfaces using various control paradigms, including pseudo-random binary excitation, nonlinear model predictive control, and reinforcement learning agents. We include several example applications in dynamics model learning, state estimation, and time-series classification to illustrate common robotics algorithms that can be benchmarked on our dataset.

Fine-Tuning of Neural Network Approximate MPC without Retraining via Bayesian Optimization

Approximate model-predictive control (AMPC) aims to imitate an MPC's behavior with a neural network, removing the need to solve an expensive optimization problem at runtime. However, during deployment, the parameters of the underlying MPC must usually be fine-tuned. This often renders AMPC impractical as it requires repeatedly generating a new dataset and retraining the neural network. Recent work addresses this problem by adapting AMPC without retraining using approximated sensitivities of the MPC's optimization problem. Currently, this adaption must be done by hand, which is labor-intensive and can be unintuitive for high-dimensional systems. To solve this issue, we propose using Bayesian optimization to tune the parameters of AMPC policies based on experimental data. By combining model-based control with direct and local learning, our approach achieves superior performance to nominal AMPC on hardware, with minimal experimentation. This allows automatic and data-efficient adaptation of AMPC to new system instances and fine-tuning to cost functions that are difficult to directly implement in MPC. We demonstrate the proposed method in hardware experiments for the swing-up maneuver on an inverted cartpole and yaw control of an under-actuated balancing unicycle robot, a challenging control problem.

Bayesian Optimization via Continual Variational Last Layer Training

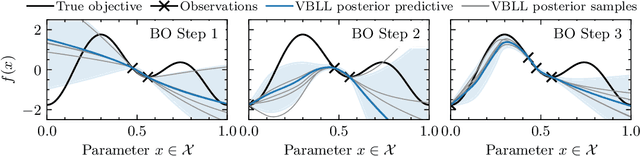
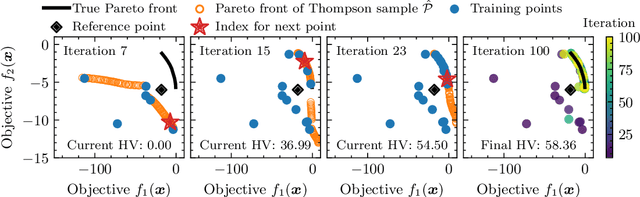
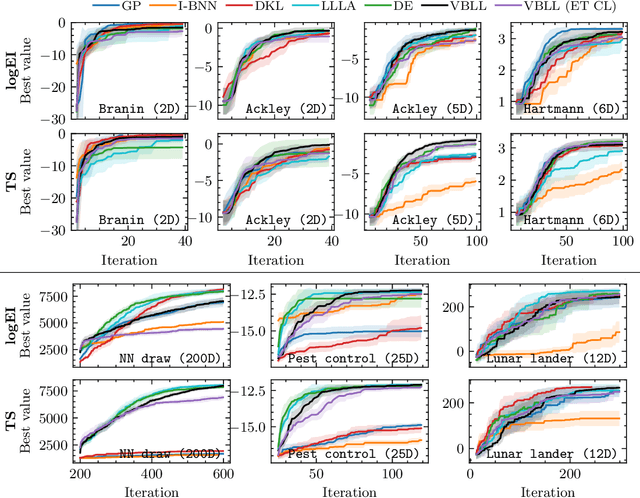
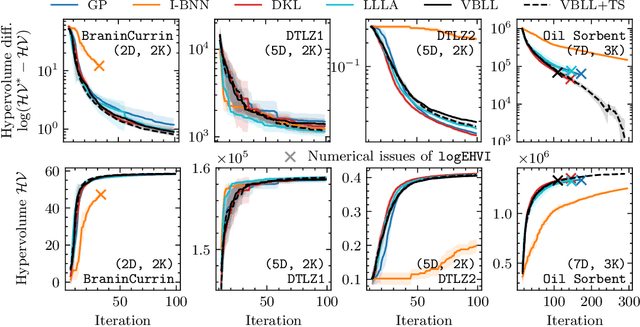
Gaussian Processes (GPs) are widely seen as the state-of-the-art surrogate models for Bayesian optimization (BO) due to their ability to model uncertainty and their performance on tasks where correlations are easily captured (such as those defined by Euclidean metrics) and their ability to be efficiently updated online. However, the performance of GPs depends on the choice of kernel, and kernel selection for complex correlation structures is often difficult or must be made bespoke. While Bayesian neural networks (BNNs) are a promising direction for higher capacity surrogate models, they have so far seen limited use due to poor performance on some problem types. In this paper, we propose an approach which shows competitive performance on many problem types, including some that BNNs typically struggle with. We build on variational Bayesian last layers (VBLLs), and connect training of these models to exact conditioning in GPs. We exploit this connection to develop an efficient online training algorithm that interleaves conditioning and optimization. Our findings suggest that VBLL networks significantly outperform GPs and other BNN architectures on tasks with complex input correlations, and match the performance of well-tuned GPs on established benchmark tasks.

Event-Triggered Time-Varying Bayesian Optimization

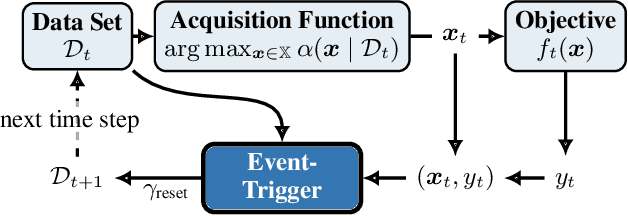
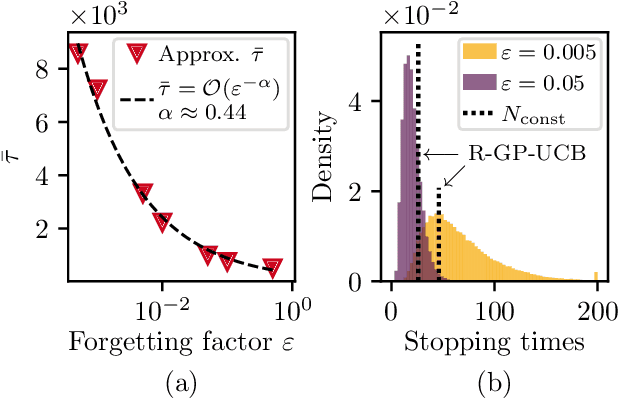
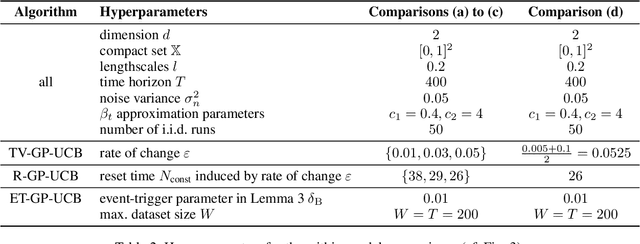
We consider the problem of sequentially optimizing a time-varying objective function using time-varying Bayesian optimization (TVBO). Here, the key challenge is to cope with old data. Current approaches to TVBO require prior knowledge of a constant rate of change. However, the rate of change is usually neither known nor constant. We propose an event-triggered algorithm, ET-GP-UCB, that detects changes in the objective function online. The event-trigger is based on probabilistic uniform error bounds used in Gaussian process regression. The trigger automatically detects when significant change in the objective functions occurs. The algorithm then adapts to the temporal change by resetting the accumulated dataset. We provide regret bounds for ET-GP-UCB and show in numerical experiments that it is competitive with state-of-the-art algorithms even though it requires no knowledge about the temporal changes. Further, ET-GP-UCB outperforms these competitive baselines if the rate of change is misspecified and we demonstrate that it is readily applicable to various settings without tuning hyperparameters.

On Controller Tuning with Time-Varying Bayesian Optimization

Changing conditions or environments can cause system dynamics to vary over time. To ensure optimal control performance, controllers should adapt to these changes. When the underlying cause and time of change is unknown, we need to rely on online data for this adaptation. In this paper, we will use time-varying Bayesian optimization (TVBO) to tune controllers online in changing environments using appropriate prior knowledge on the control objective and its changes. Two properties are characteristic of many online controller tuning problems: First, they exhibit incremental and lasting changes in the objective due to changes to the system dynamics, e.g., through wear and tear. Second, the optimization problem is convex in the tuning parameters. Current TVBO methods do not explicitly account for these properties, resulting in poor tuning performance and many unstable controllers through over-exploration of the parameter space. We propose a novel TVBO forgetting strategy using Uncertainty-Injection (UI), which incorporates the assumption of incremental and lasting changes. The control objective is modeled as a spatio-temporal Gaussian process (GP) with UI through a Wiener process in the temporal domain. Further, we explicitly model the convexity assumptions in the spatial dimension through GP models with linear inequality constraints. In numerical experiments, we show that our model outperforms the state-of-the-art method in TVBO, exhibiting reduced regret and fewer unstable parameter configurations.