Risk-Sensitive Soft Actor-Critic for Robust Deep Reinforcement Learning under Distribution Shifts
Paper and Code
Feb 15, 2024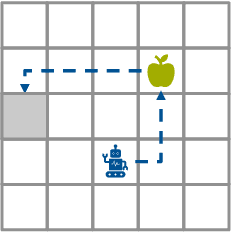
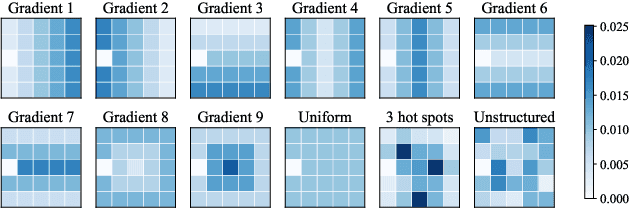
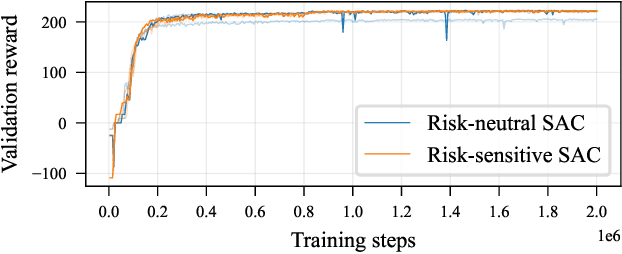
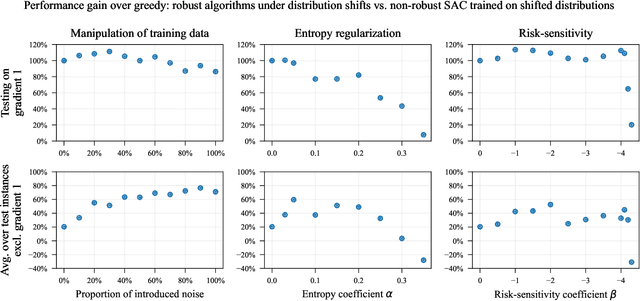
We study the robustness of deep reinforcement learning algorithms against distribution shifts within contextual multi-stage stochastic combinatorial optimization problems from the operations research domain. In this context, risk-sensitive algorithms promise to learn robust policies. While this field is of general interest to the reinforcement learning community, most studies up-to-date focus on theoretical results rather than real-world performance. With this work, we aim to bridge this gap by formally deriving a novel risk-sensitive deep reinforcement learning algorithm while providing numerical evidence for its efficacy. Specifically, we introduce discrete Soft Actor-Critic for the entropic risk measure by deriving a version of the Bellman equation for the respective Q-values. We establish a corresponding policy improvement result and infer a practical algorithm. We introduce an environment that represents typical contextual multi-stage stochastic combinatorial optimization problems and perform numerical experiments to empirically validate our algorithm's robustness against realistic distribution shifts, without compromising performance on the training distribution. We show that our algorithm is superior to risk-neutral Soft Actor-Critic as well as to two benchmark approaches for robust deep reinforcement learning. Thereby, we provide the first structured analysis on the robustness of reinforcement learning under distribution shifts in the realm of contextual multi-stage stochastic combinatorial optimization problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge