Applications of fractional calculus in learned optimization
Paper and Code
Nov 22, 2024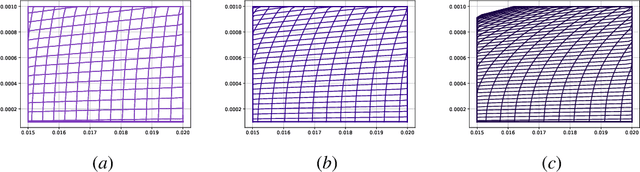
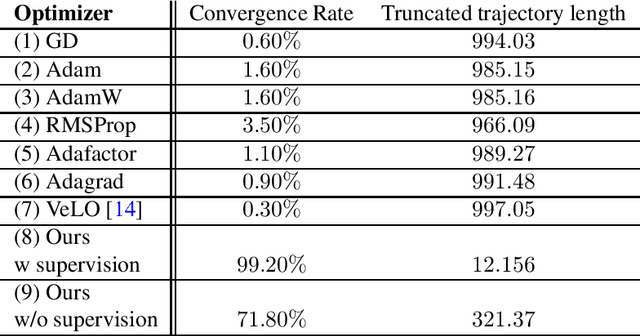
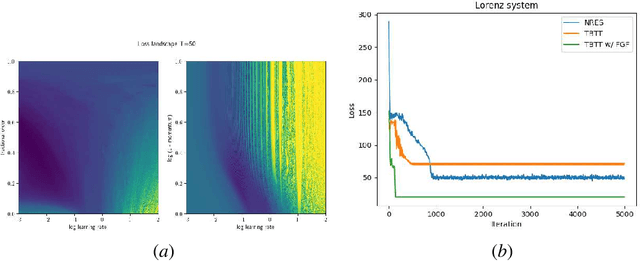
Fractional gradient descent has been studied extensively, with a focus on its ability to extend traditional gradient descent methods by incorporating fractional-order derivatives. This approach allows for more flexibility in navigating complex optimization landscapes and offers advantages in certain types of problems, particularly those involving non-linearities and chaotic dynamics. Yet, the challenge of fine-tuning the fractional order parameters remains unsolved. In this work, we demonstrate that it is possible to train a neural network to predict the order of the gradient effectively.
* NeurIPS Workshop on Optimization for Machine Learning
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge