Training Language Models on the Knowledge Graph: Insights on Hallucinations and Their Detectability

While many capabilities of language models (LMs) improve with increased training budget, the influence of scale on hallucinations is not yet fully understood. Hallucinations come in many forms, and there is no universally accepted definition. We thus focus on studying only those hallucinations where a correct answer appears verbatim in the training set. To fully control the training data content, we construct a knowledge graph (KG)-based dataset, and use it to train a set of increasingly large LMs. We find that for a fixed dataset, larger and longer-trained LMs hallucinate less. However, hallucinating on $\leq5$% of the training data requires an order of magnitude larger model, and thus an order of magnitude more compute, than Hoffmann et al. (2022) reported was optimal. Given this costliness, we study how hallucination detectors depend on scale. While we see detector size improves performance on fixed LM's outputs, we find an inverse relationship between the scale of the LM and the detectability of its hallucinations.

Scaling Exponents Across Parameterizations and Optimizers

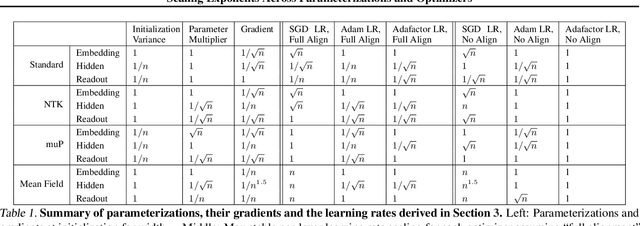
Robust and effective scaling of models from small to large width typically requires the precise adjustment of many algorithmic and architectural details, such as parameterization and optimizer choices. In this work, we propose a new perspective on parameterization by investigating a key assumption in prior work about the alignment between parameters and data and derive new theoretical results under weaker assumptions and a broader set of optimizers. Our extensive empirical investigation includes tens of thousands of models trained with all combinations of three optimizers, four parameterizations, several alignment assumptions, more than a dozen learning rates, and fourteen model sizes up to 26.8B parameters. We find that the best learning rate scaling prescription would often have been excluded by the assumptions in prior work. Our results show that all parameterizations, not just maximal update parameterization (muP), can achieve hyperparameter transfer; moreover, our novel per-layer learning rate prescription for standard parameterization outperforms muP. Finally, we demonstrate that an overlooked aspect of parameterization, the epsilon parameter in Adam, must be scaled correctly to avoid gradient underflow and propose Adam-atan2, a new numerically stable, scale-invariant version of Adam that eliminates the epsilon hyperparameter entirely.

4+3 Phases of Compute-Optimal Neural Scaling Laws

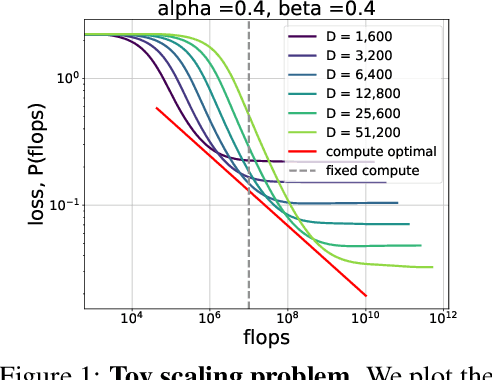
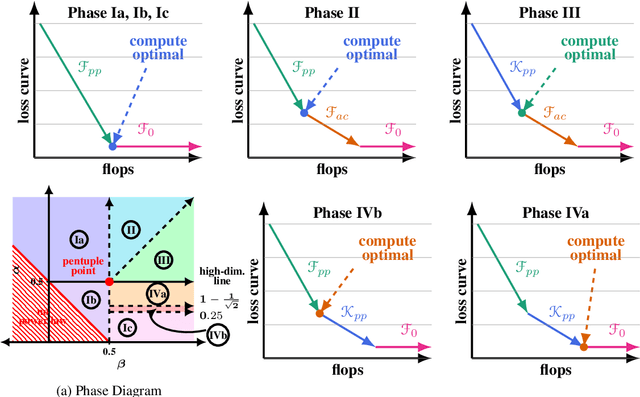
We consider the three parameter solvable neural scaling model introduced by Maloney, Roberts, and Sully. The model has three parameters: data complexity, target complexity, and model-parameter-count. We use this neural scaling model to derive new predictions about the compute-limited, infinite-data scaling law regime. To train the neural scaling model, we run one-pass stochastic gradient descent on a mean-squared loss. We derive a representation of the loss curves which holds over all iteration counts and improves in accuracy as the model parameter count grows. We then analyze the compute-optimal model-parameter-count, and identify 4 phases (+3 subphases) in the data-complexity/target-complexity phase-plane. The phase boundaries are determined by the relative importance of model capacity, optimizer noise, and embedding of the features. We furthermore derive, with mathematical proof and extensive numerical evidence, the scaling-law exponents in all of these phases, in particular computing the optimal model-parameter-count as a function of floating point operation budget.

Beyond Human Data: Scaling Self-Training for Problem-Solving with Language Models

Fine-tuning language models~(LMs) on human-generated data remains a prevalent practice. However, the performance of such models is often limited by the quantity and diversity of high-quality human data. In this paper, we explore whether we can go beyond human data on tasks where we have access to scalar feedback, for example, on math problems where one can verify correctness. To do so, we investigate a simple self-training method based on expectation-maximization, which we call ReST$^{EM}$, where we (1) generate samples from the model and filter them using binary feedback, (2) fine-tune the model on these samples, and (3) repeat this process a few times. Testing on advanced MATH reasoning and APPS coding benchmarks using PaLM-2 models, we find that ReST$^{EM}$ scales favorably with model size and significantly surpasses fine-tuning only on human data. Overall, our findings suggest self-training with feedback can substantially reduce dependence on human-generated data.

Frontier Language Models are not Robust to Adversarial Arithmetic, or "What do I need to say so you agree 2+2=5?

We introduce and study the problem of adversarial arithmetic, which provides a simple yet challenging testbed for language model alignment. This problem is comprised of arithmetic questions posed in natural language, with an arbitrary adversarial string inserted before the question is complete. Even in the simple setting of 1-digit addition problems, it is easy to find adversarial prompts that make all tested models (including PaLM2, GPT4, Claude2) misbehave, and even to steer models to a particular wrong answer. We additionally provide a simple algorithm for finding successful attacks by querying those same models, which we name "prompt inversion rejection sampling" (PIRS). We finally show that models can be partially hardened against these attacks via reinforcement learning and via agentic constitutional loops. However, we were not able to make a language model fully robust against adversarial arithmetic attacks.

Small-scale proxies for large-scale Transformer training instabilities

Teams that have trained large Transformer-based models have reported training instabilities at large scale that did not appear when training with the same hyperparameters at smaller scales. Although the causes of such instabilities are of scientific interest, the amount of resources required to reproduce them has made investigation difficult. In this work, we seek ways to reproduce and study training stability and instability at smaller scales. First, we focus on two sources of training instability described in previous work: the growth of logits in attention layers (Dehghani et al., 2023) and divergence of the output logits from the log probabilities (Chowdhery et al., 2022). By measuring the relationship between learning rate and loss across scales, we show that these instabilities also appear in small models when training at high learning rates, and that mitigations previously employed at large scales are equally effective in this regime. This prompts us to investigate the extent to which other known optimizer and model interventions influence the sensitivity of the final loss to changes in the learning rate. To this end, we study methods such as warm-up, weight decay, and the $\mu$Param (Yang et al., 2022), and combine techniques to train small models that achieve similar losses across orders of magnitude of learning rate variation. Finally, to conclude our exploration we study two cases where instabilities can be predicted before they emerge by examining the scaling behavior of model activation and gradient norms.

Fast Neural Kernel Embeddings for General Activations

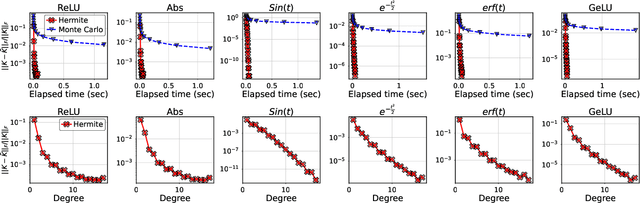
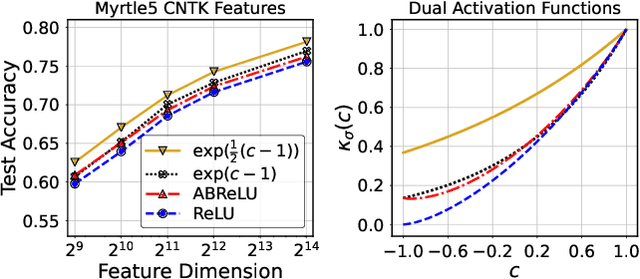
Infinite width limit has shed light on generalization and optimization aspects of deep learning by establishing connections between neural networks and kernel methods. Despite their importance, the utility of these kernel methods was limited in large-scale learning settings due to their (super-)quadratic runtime and memory complexities. Moreover, most prior works on neural kernels have focused on the ReLU activation, mainly due to its popularity but also due to the difficulty of computing such kernels for general activations. In this work, we overcome such difficulties by providing methods to work with general activations. First, we compile and expand the list of activation functions admitting exact dual activation expressions to compute neural kernels. When the exact computation is unknown, we present methods to effectively approximate them. We propose a fast sketching method that approximates any multi-layered Neural Network Gaussian Process (NNGP) kernel and Neural Tangent Kernel (NTK) matrices for a wide range of activation functions, going beyond the commonly analyzed ReLU activation. This is done by showing how to approximate the neural kernels using the truncated Hermite expansion of any desired activation functions. While most prior works require data points on the unit sphere, our methods do not suffer from such limitations and are applicable to any dataset of points in $\mathbb{R}^d$. Furthermore, we provide a subspace embedding for NNGP and NTK matrices with near input-sparsity runtime and near-optimal target dimension which applies to any \emph{homogeneous} dual activation functions with rapidly convergent Taylor expansion. Empirically, with respect to exact convolutional NTK (CNTK) computation, our method achieves $106\times$ speedup for approximate CNTK of a 5-layer Myrtle network on CIFAR-10 dataset.

Synergy and Symmetry in Deep Learning: Interactions between the Data, Model, and Inference Algorithm

Although learning in high dimensions is commonly believed to suffer from the curse of dimensionality, modern machine learning methods often exhibit an astonishing power to tackle a wide range of challenging real-world learning problems without using abundant amounts of data. How exactly these methods break this curse remains a fundamental open question in the theory of deep learning. While previous efforts have investigated this question by studying the data (D), model (M), and inference algorithm (I) as independent modules, in this paper, we analyze the triplet (D, M, I) as an integrated system and identify important synergies that help mitigate the curse of dimensionality. We first study the basic symmetries associated with various learning algorithms (M, I), focusing on four prototypical architectures in deep learning: fully-connected networks (FCN), locally-connected networks (LCN), and convolutional networks with and without pooling (GAP/VEC). We find that learning is most efficient when these symmetries are compatible with those of the data distribution and that performance significantly deteriorates when any member of the (D, M, I) triplet is inconsistent or suboptimal.

Precise Learning Curves and Higher-Order Scaling Limits for Dot Product Kernel Regression

As modern machine learning models continue to advance the computational frontier, it has become increasingly important to develop precise estimates for expected performance improvements under different model and data scaling regimes. Currently, theoretical understanding of the learning curves that characterize how the prediction error depends on the number of samples is restricted to either large-sample asymptotics ($m\to\infty$) or, for certain simple data distributions, to the high-dimensional asymptotics in which the number of samples scales linearly with the dimension ($m\propto d$). There is a wide gulf between these two regimes, including all higher-order scaling relations $m\propto d^r$, which are the subject of the present paper. We focus on the problem of kernel ridge regression for dot-product kernels and present precise formulas for the test error, bias, and variance, for data drawn uniformly from the sphere in the $r$th-order asymptotic scaling regime $m\to\infty$ with $m/d^r$ held constant. We observe a peak in the learning curve whenever $m \approx d^r/r!$ for any integer $r$, leading to multiple sample-wise descent and nontrivial behavior at multiple scales.

Eigenspace Restructuring: a Principle of Space and Frequency in Neural Networks

Understanding the fundamental principles behind the massive success of neural networks is one of the most important open questions in deep learning. However, due to the highly complex nature of the problem, progress has been relatively slow. In this note, through the lens of infinite-width networks, a.k.a. neural kernels, we present one such principle resulting from hierarchical localities. It is well-known that the eigenstructure of infinite-width multilayer perceptrons (MLPs) depends solely on the concept frequency, which measures the order of interactions. We show that the topologies from deep convolutional networks (CNNs) restructure the associated eigenspaces into finer subspaces. In addition to frequency, the new structure also depends on the concept space, which measures the spatial distance among nonlinear interaction terms. The resulting fine-grained eigenstructure dramatically improves the network's learnability, empowering them to simultaneously model a much richer class of interactions, including Long-Range-Low-Frequency interactions, Short-Range-High-Frequency interactions, and various interpolations and extrapolations in-between. Additionally, model scaling can improve the resolutions of interpolations and extrapolations and, therefore, the network's learnability. Finally, we prove a sharp characterization of the generalization error for infinite-width CNNs of any depth in the high-dimensional setting. Two corollaries follow: (1) infinite-width deep CNNs can break the curse of dimensionality without losing their expressivity, and (2) scaling improves performance in both the finite and infinite data regimes.