Fast Neural Kernel Embeddings for General Activations
Paper and Code
Sep 09, 2022
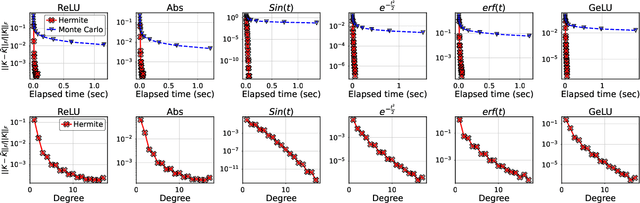
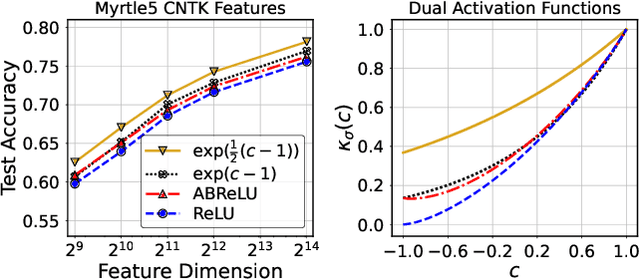

Infinite width limit has shed light on generalization and optimization aspects of deep learning by establishing connections between neural networks and kernel methods. Despite their importance, the utility of these kernel methods was limited in large-scale learning settings due to their (super-)quadratic runtime and memory complexities. Moreover, most prior works on neural kernels have focused on the ReLU activation, mainly due to its popularity but also due to the difficulty of computing such kernels for general activations. In this work, we overcome such difficulties by providing methods to work with general activations. First, we compile and expand the list of activation functions admitting exact dual activation expressions to compute neural kernels. When the exact computation is unknown, we present methods to effectively approximate them. We propose a fast sketching method that approximates any multi-layered Neural Network Gaussian Process (NNGP) kernel and Neural Tangent Kernel (NTK) matrices for a wide range of activation functions, going beyond the commonly analyzed ReLU activation. This is done by showing how to approximate the neural kernels using the truncated Hermite expansion of any desired activation functions. While most prior works require data points on the unit sphere, our methods do not suffer from such limitations and are applicable to any dataset of points in $\mathbb{R}^d$. Furthermore, we provide a subspace embedding for NNGP and NTK matrices with near input-sparsity runtime and near-optimal target dimension which applies to any \emph{homogeneous} dual activation functions with rapidly convergent Taylor expansion. Empirically, with respect to exact convolutional NTK (CNTK) computation, our method achieves $106\times$ speedup for approximate CNTK of a 5-layer Myrtle network on CIFAR-10 dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge