Amin Karbasi
EPFL
Think Before You Retrieve: Learning Test-Time Adaptive Search with Small Language Models
Nov 10, 2025Abstract:Effective information retrieval requires reasoning over partial evidence and refining strategies as information emerges. Yet current approaches fall short: neural retrievers lack reasoning capabilities, large language models (LLMs) provide semantic depth but at prohibitive cost, and query rewriting or decomposition limits improvement to static transformations. As a result, existing methods fail to capture the iterative dynamics of exploration, feedback, and revision that complex user queries demand. We introduce Orion, a training framework that enables compact models (350M-1.2B parameters) to perform iterative retrieval through learned search strategies. Orion combines: (1) synthetic trajectory generation and supervised fine-tuning to encourage diverse exploration patterns in models, (2) reinforcement learning (RL) that rewards effective query refinement and backtracking behaviors, and (3) inference-time beam search algorithms that exploit the self-reflection capabilities learned during RL. Despite using only 3% of the training data available, our 1.2B model achieves 77.6% success on SciFact (vs. 72.6% for prior retrievers), 25.2% on BRIGHT (vs. 22.1%), 63.2% on NFCorpus (vs. 57.8%), and remains competitive on FEVER, HotpotQA, and MSMarco. It outperforms retrievers up to 200-400x larger on five of six benchmarks. These findings suggest that retrieval performance can emerge from learned strategies, not just model scale, when models are trained to search, reflect, and revise.
Llama-3.1-FoundationAI-SecurityLLM-Base-8B Technical Report
Apr 28, 2025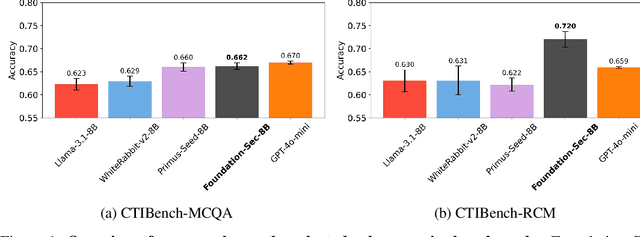
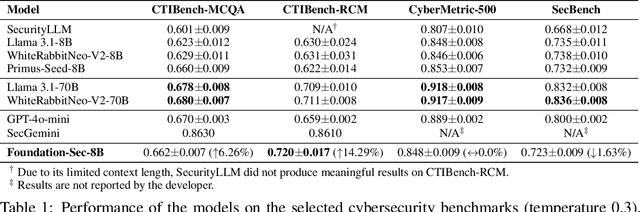
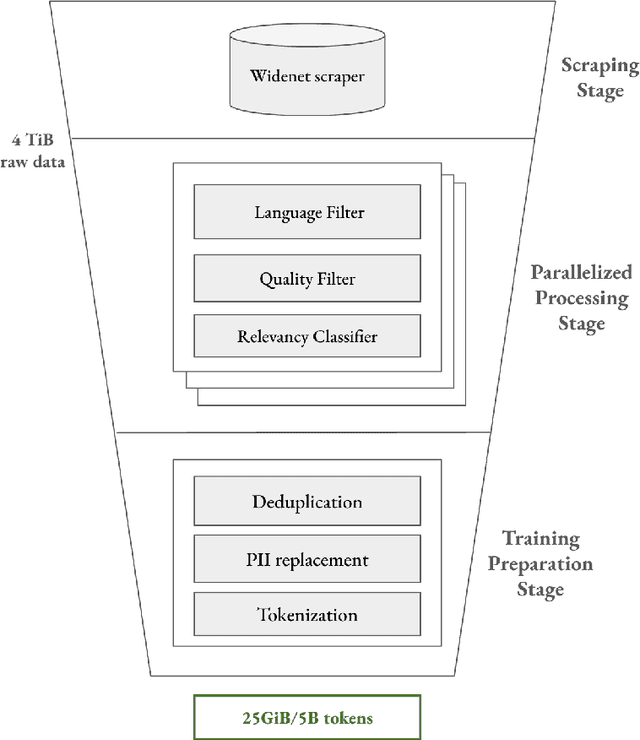

Abstract:As transformer-based large language models (LLMs) increasingly permeate society, they have revolutionized domains such as software engineering, creative writing, and digital arts. However, their adoption in cybersecurity remains limited due to challenges like scarcity of specialized training data and complexity of representing cybersecurity-specific knowledge. To address these gaps, we present Foundation-Sec-8B, a cybersecurity-focused LLM built on the Llama 3.1 architecture and enhanced through continued pretraining on a carefully curated cybersecurity corpus. We evaluate Foundation-Sec-8B across both established and new cybersecurity benchmarks, showing that it matches Llama 3.1-70B and GPT-4o-mini in certain cybersecurity-specific tasks. By releasing our model to the public, we aim to accelerate progress and adoption of AI-driven tools in both public and private cybersecurity contexts.
(Im)possibility of Automated Hallucination Detection in Large Language Models
Apr 23, 2025Abstract:Is automated hallucination detection possible? In this work, we introduce a theoretical framework to analyze the feasibility of automatically detecting hallucinations produced by large language models (LLMs). Inspired by the classical Gold-Angluin framework for language identification and its recent adaptation to language generation by Kleinberg and Mullainathan, we investigate whether an algorithm, trained on examples drawn from an unknown target language $K$ (selected from a countable collection) and given access to an LLM, can reliably determine whether the LLM's outputs are correct or constitute hallucinations. First, we establish an equivalence between hallucination detection and the classical task of language identification. We prove that any hallucination detection method can be converted into a language identification method, and conversely, algorithms solving language identification can be adapted for hallucination detection. Given the inherent difficulty of language identification, this implies that hallucination detection is fundamentally impossible for most language collections if the detector is trained using only correct examples from the target language. Second, we show that the use of expert-labeled feedback, i.e., training the detector with both positive examples (correct statements) and negative examples (explicitly labeled incorrect statements), dramatically changes this conclusion. Under this enriched training regime, automated hallucination detection becomes possible for all countable language collections. These results highlight the essential role of expert-labeled examples in training hallucination detectors and provide theoretical support for feedback-based methods, such as reinforcement learning with human feedback (RLHF), which have proven critical for reliable LLM deployment.
Learning Task Representations from In-Context Learning
Feb 08, 2025Abstract:Large language models (LLMs) have demonstrated remarkable proficiency in in-context learning (ICL), where models adapt to new tasks through example-based prompts without requiring parameter updates. However, understanding how tasks are internally encoded and generalized remains a challenge. To address some of the empirical and technical gaps in the literature, we introduce an automated formulation for encoding task information in ICL prompts as a function of attention heads within the transformer architecture. This approach computes a single task vector as a weighted sum of attention heads, with the weights optimized causally via gradient descent. Our findings show that existing methods fail to generalize effectively to modalities beyond text. In response, we also design a benchmark to evaluate whether a task vector can preserve task fidelity in functional regression tasks. The proposed method successfully extracts task-specific information from in-context demonstrations and excels in both text and regression tasks, demonstrating its generalizability across modalities. Moreover, ablation studies show that our method's effectiveness stems from aligning the distribution of the last hidden state with that of an optimally performing in-context-learned model.
PolarQuant: Quantizing KV Caches with Polar Transformation
Feb 04, 2025Abstract:Large language models (LLMs) require significant memory to store Key-Value (KV) embeddings in their KV cache, especially when handling long-range contexts. Quantization of these KV embeddings is a common technique to reduce memory consumption. This work introduces PolarQuant, a novel quantization method employing random preconditioning and polar transformation. Our method transforms the KV embeddings into polar coordinates using an efficient recursive algorithm and then quantizes resulting angles. Our key insight is that, after random preconditioning, the angles in the polar representation exhibit a tightly bounded and highly concentrated distribution with an analytically computable form. This nice distribution eliminates the need for explicit normalization, a step required by traditional quantization methods which introduces significant memory overhead because quantization parameters (e.g., zero point and scale) must be stored in full precision per each data block. PolarQuant bypasses this normalization step, enabling substantial memory savings. The long-context evaluation demonstrates that PolarQuant compresses the KV cache by over x4.2 while achieving the best quality scores compared to the state-of-the-art methods.
Adversarial Reasoning at Jailbreaking Time
Feb 03, 2025Abstract:As large language models (LLMs) are becoming more capable and widespread, the study of their failure cases is becoming increasingly important. Recent advances in standardizing, measuring, and scaling test-time compute suggest new methodologies for optimizing models to achieve high performance on hard tasks. In this paper, we apply these advances to the task of model jailbreaking: eliciting harmful responses from aligned LLMs. We develop an adversarial reasoning approach to automatic jailbreaking via test-time computation that achieves SOTA attack success rates (ASR) against many aligned LLMs, even the ones that aim to trade inference-time compute for adversarial robustness. Our approach introduces a new paradigm in understanding LLM vulnerabilities, laying the foundation for the development of more robust and trustworthy AI systems.
Criteria and Bias of Parameterized Linear Regression under Edge of Stability Regime
Dec 11, 2024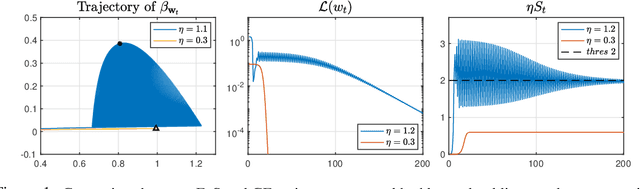
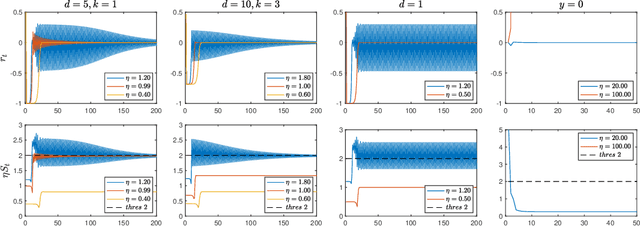

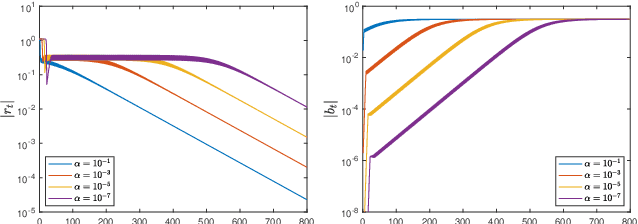
Abstract:Classical optimization theory requires a small step-size for gradient-based methods to converge. Nevertheless, recent findings challenge the traditional idea by empirically demonstrating Gradient Descent (GD) converges even when the step-size $\eta$ exceeds the threshold of $2/L$, where $L$ is the global smooth constant. This is usually known as the Edge of Stability (EoS) phenomenon. A widely held belief suggests that an objective function with subquadratic growth plays an important role in incurring EoS. In this paper, we provide a more comprehensive answer by considering the task of finding linear interpolator $\beta \in R^{d}$ for regression with loss function $l(\cdot)$, where $\beta$ admits parameterization as $\beta = w^2_{+} - w^2_{-}$. Contrary to the previous work that suggests a subquadratic $l$ is necessary for EoS, our novel finding reveals that EoS occurs even when $l$ is quadratic under proper conditions. This argument is made rigorous by both empirical and theoretical evidence, demonstrating the GD trajectory converges to a linear interpolator in a non-asymptotic way. Moreover, the model under quadratic $l$, also known as a depth-$2$ diagonal linear network, remains largely unexplored under the EoS regime. Our analysis then sheds some new light on the implicit bias of diagonal linear networks when a larger step-size is employed, enriching the understanding of EoS on more practical models.
Procurement Auctions via Approximately Optimal Submodular Optimization
Nov 20, 2024Abstract:We study procurement auctions, where an auctioneer seeks to acquire services from strategic sellers with private costs. The quality of services is measured by a submodular function known to the auctioneer. Our goal is to design computationally efficient procurement auctions that (approximately) maximize the difference between the quality of the acquired services and the total cost of the sellers, while ensuring incentive compatibility (IC), individual rationality (IR) for sellers, and non-negative surplus (NAS) for the auctioneer. Our contributions are twofold: (i) we provide an improved analysis of existing algorithms for non-positive submodular function maximization, and (ii) we design efficient frameworks that transform submodular optimization algorithms into mechanisms that are IC, IR, NAS, and approximation-preserving. These frameworks apply to both the offline setting, where all sellers' bids and services are available simultaneously, and the online setting, where sellers arrive in an adversarial order, requiring the auctioneer to make irrevocable decisions. We also explore whether state-of-the-art submodular optimization algorithms can be converted into descending auctions in adversarial settings, where the schedule of descending prices is determined by an adversary. We show that a submodular optimization algorithm satisfying bi-criteria $(1/2, 1)$-approximation in welfare can be effectively adapted to a descending auction. Additionally, we establish a connection between descending auctions and online submodular optimization. Finally, we demonstrate the practical applications of our frameworks by instantiating them with state-of-the-art submodular optimization algorithms and empirically comparing their welfare performance on publicly available datasets with thousands of sellers.
A Flow-based Truncated Denoising Diffusion Model for Super-resolution Magnetic Resonance Spectroscopic Imaging
Oct 25, 2024Abstract:Magnetic Resonance Spectroscopic Imaging (MRSI) is a non-invasive imaging technique for studying metabolism and has become a crucial tool for understanding neurological diseases, cancers and diabetes. High spatial resolution MRSI is needed to characterize lesions, but in practice MRSI is acquired at low resolution due to time and sensitivity restrictions caused by the low metabolite concentrations. Therefore, there is an imperative need for a post-processing approach to generate high-resolution MRSI from low-resolution data that can be acquired fast and with high sensitivity. Deep learning-based super-resolution methods provided promising results for improving the spatial resolution of MRSI, but they still have limited capability to generate accurate and high-quality images. Recently, diffusion models have demonstrated superior learning capability than other generative models in various tasks, but sampling from diffusion models requires iterating through a large number of diffusion steps, which is time-consuming. This work introduces a Flow-based Truncated Denoising Diffusion Model (FTDDM) for super-resolution MRSI, which shortens the diffusion process by truncating the diffusion chain, and the truncated steps are estimated using a normalizing flow-based network. The network is conditioned on upscaling factors to enable multi-scale super-resolution. To train and evaluate the deep learning models, we developed a 1H-MRSI dataset acquired from 25 high-grade glioma patients. We demonstrate that FTDDM outperforms existing generative models while speeding up the sampling process by over 9-fold compared to the baseline diffusion model. Neuroradiologists' evaluations confirmed the clinical advantages of our method, which also supports uncertainty estimation and sharpness adjustment, extending its potential clinical applications.
* Accepted by Medical Image Analysis (MedIA)
TSDS: Data Selection for Task-Specific Model Finetuning
Oct 23, 2024



Abstract:Finetuning foundation models for specific tasks is an emerging paradigm in modern machine learning. The efficacy of task-specific finetuning largely depends on the selection of appropriate training data. We present TSDS (Task-Specific Data Selection), a framework to select data for task-specific model finetuning, guided by a small but representative set of examples from the target task. To do so, we formulate data selection for task-specific finetuning as an optimization problem with a distribution alignment loss based on optimal transport to capture the discrepancy between the selected data and the target distribution. In addition, we add a regularizer to encourage the diversity of the selected data and incorporate kernel density estimation into the regularizer to reduce the negative effects of near-duplicates among the candidate data. We connect our optimization problem to nearest neighbor search and design efficient algorithms to compute the optimal solution based on approximate nearest neighbor search techniques. We evaluate our method on data selection for both continued pretraining and instruction tuning of language models. We show that instruction tuning using data selected by our method with a 1% selection ratio often outperforms using the full dataset and beats the baseline selection methods by 1.5 points in F1 score on average.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge