Towards X-embodiment safety: A control theory perspective on transferring safety certificates across dynamical systems

Control barrier functions (CBFs) provide a powerful tool for enforcing safety constraints in control systems, but their direct application to complex, high-dimensional dynamics is often challenging. In many settings, safety certificates are more naturally designed for simplified or alternative system models that do not exactly match the dynamics of interest. This paper addresses the problem of transferring safety guarantees between dynamical systems with mismatched dynamics. We propose a transferred control barrier function (tCBF) framework that enables safety constraints defined on one system to be systematically enforced on another system using a simulation function and an explicit margin term. The resulting transferred barrier accounts for model mismatch and induces a safety condition that can be enforced on the target system via a quadratic-program-based safety filter. The proposed approach is general and does not require the two systems to share the same state dimension or dynamics. We demonstrate the effectiveness of the framework on a quadrotor navigation task with the transferred barrier ensuring collision avoidance for the target system, while remaining minimally invasive to a nominal controller. These results highlight the potential of transferred control barrier functions as a general mechanism for enforcing safety across heterogeneous dynamical systems.

eCP: Informative uncertainty quantification via Equivariantized Conformal Prediction with pre-trained models

We study the effect of group symmetrization of pre-trained models on conformal prediction (CP), a post-hoc, distribution-free, finite-sample method of uncertainty quantification that offers formal coverage guarantees under the assumption of data exchangeability. Unfortunately, CP uncertainty regions can grow significantly in long horizon missions, rendering the statistical guarantees uninformative. To that end, we propose infusing CP with geometric information via group-averaging of the pretrained predictor to distribute the non-conformity mass across the orbits. Each sample now is treated as a representative of an orbit, thus uncertainty can be mitigated by other samples entangled to it via the orbit inducing elements of the symmetry group. Our approach provably yields contracted non-conformity scores in increasing convex order, implying improved exponential-tail bounds and sharper conformal prediction sets in expectation, especially at high confidence levels. We then propose an experimental design to test these theoretical claims in pedestrian trajectory prediction.

Deep Equivariant Multi-Agent Control Barrier Functions

With multi-agent systems increasingly deployed autonomously at scale in complex environments, ensuring safety of the data-driven policies is critical. Control Barrier Functions have emerged as an effective tool for enforcing safety constraints, yet existing learning-based methods often lack in scalability, generalization and sampling efficiency as they overlook inherent geometric structures of the system. To address this gap, we introduce symmetries-infused distributed Control Barrier Functions, enforcing the satisfaction of intrinsic symmetries on learnable graph-based safety certificates. We theoretically motivate the need for equivariant parametrization of CBFs and policies, and propose a simple, yet efficient and adaptable methodology for constructing such equivariant group-modular networks via the compatible group actions. This approach encodes safety constraints in a distributed data-efficient manner, enabling zero-shot generalization to larger and denser swarms. Through extensive simulations on multi-robot navigation tasks, we demonstrate that our method outperforms state-of-the-art baselines in terms of safety, scalability, and task success rates, highlighting the importance of embedding symmetries in safe distributed neural policies.

Conformal Prediction Beyond the Seen: A Missing Mass Perspective for Uncertainty Quantification in Generative Models

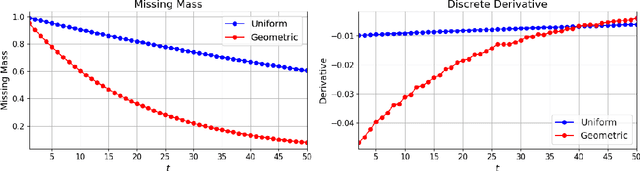
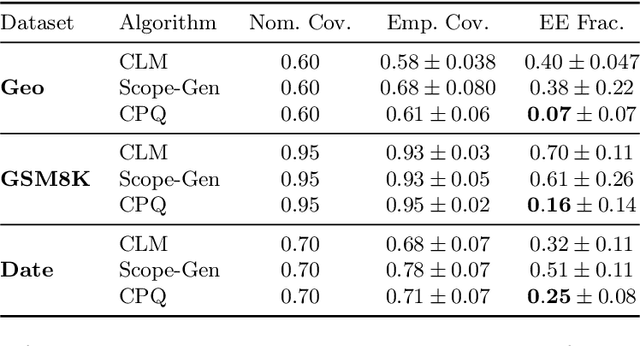
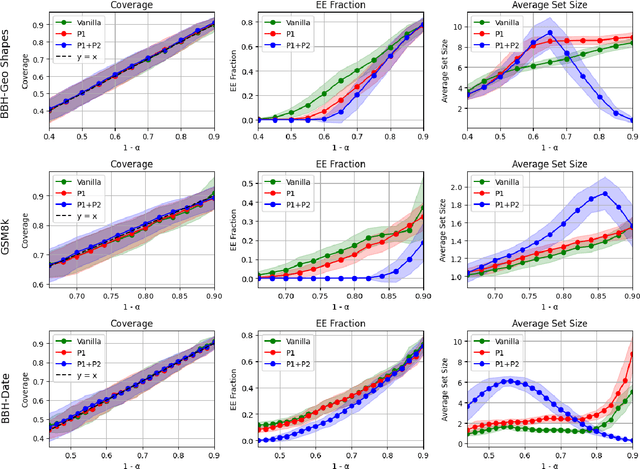
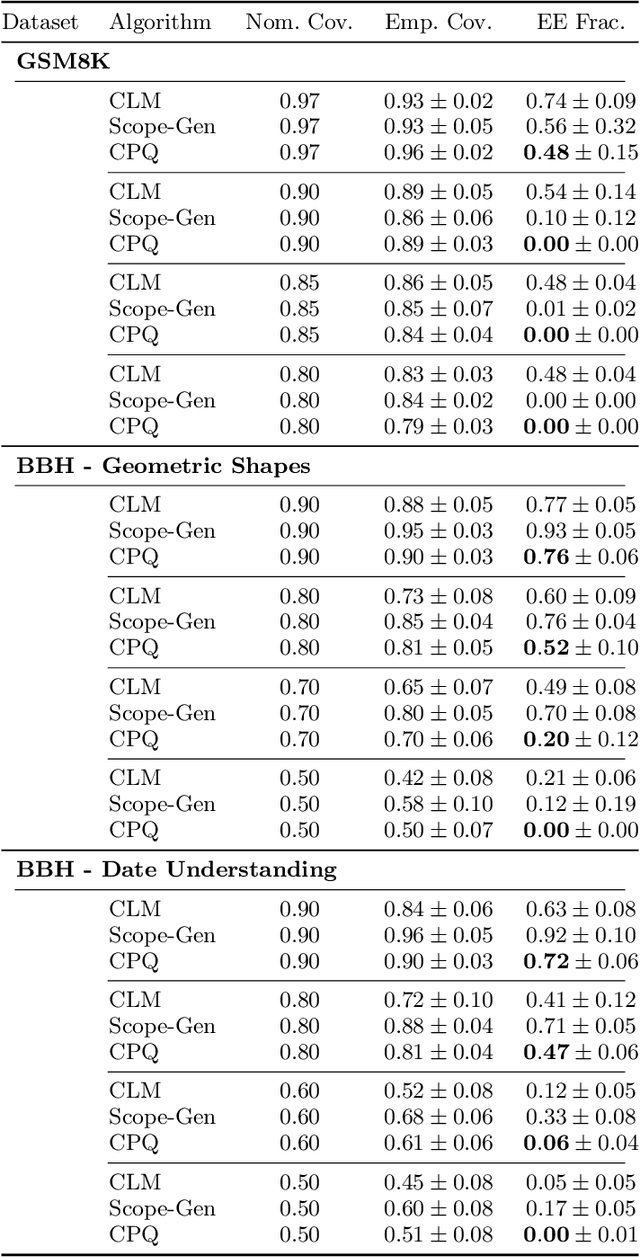
Uncertainty quantification (UQ) is essential for safe deployment of generative AI models such as large language models (LLMs), especially in high stakes applications. Conformal prediction (CP) offers a principled uncertainty quantification framework, but classical methods focus on regression and classification, relying on geometric distances or softmax scores: tools that presuppose structured outputs. We depart from this paradigm by studying CP in a query only setting, where prediction sets must be constructed solely from finite queries to a black box generative model, introducing a new trade off between coverage, test time query budget, and informativeness. We introduce Conformal Prediction with Query Oracle (CPQ), a framework characterizing the optimal interplay between these objectives. Our finite sample algorithm is built on two core principles: one governs the optimal query policy, and the other defines the optimal mapping from queried samples to prediction sets. Remarkably, both are rooted in the classical missing mass problem in statistics. Specifically, the optimal query policy depends on the rate of decay, or the derivative, of the missing mass, for which we develop a novel estimator. Meanwhile, the optimal mapping hinges on the missing mass itself, which we estimate using Good Turing estimators. We then turn our focus to implementing our method for language models, where outputs are vast, variable, and often under specified. Fine grained experiments on three real world open ended tasks and two LLMs, show CPQ applicability to any black box LLM and highlight: (1) individual contribution of each principle to CPQ performance, and (2) CPQ ability to yield significantly more informative prediction sets than existing conformal methods for language uncertainty quantification.

Likelihood-Ratio Regularized Quantile Regression: Adapting Conformal Prediction to High-Dimensional Covariate Shifts

We consider the problem of conformal prediction under covariate shift. Given labeled data from a source domain and unlabeled data from a covariate shifted target domain, we seek to construct prediction sets with valid marginal coverage in the target domain. Most existing methods require estimating the unknown likelihood ratio function, which can be prohibitive for high-dimensional data such as images. To address this challenge, we introduce the likelihood ratio regularized quantile regression (LR-QR) algorithm, which combines the pinball loss with a novel choice of regularization in order to construct a threshold function without directly estimating the unknown likelihood ratio. We show that the LR-QR method has coverage at the desired level in the target domain, up to a small error term that we can control. Our proofs draw on a novel analysis of coverage via stability bounds from learning theory. Our experiments demonstrate that the LR-QR algorithm outperforms existing methods on high-dimensional prediction tasks, including a regression task for the Communities and Crime dataset, and an image classification task from the WILDS repository.

Decision Theoretic Foundations for Conformal Prediction: Optimal Uncertainty Quantification for Risk-Averse Agents

A fundamental question in data-driven decision making is how to quantify the uncertainty of predictions in ways that can usefully inform downstream action. This interface between prediction uncertainty and decision-making is especially important in risk-sensitive domains, such as medicine. In this paper, we develop decision-theoretic foundations that connect uncertainty quantification using prediction sets with risk-averse decision-making. Specifically, we answer three fundamental questions: (1) What is the correct notion of uncertainty quantification for risk-averse decision makers? We prove that prediction sets are optimal for decision makers who wish to optimize their value at risk. (2) What is the optimal policy that a risk averse decision maker should use to map prediction sets to actions? We show that a simple max-min decision policy is optimal for risk-averse decision makers. Finally, (3) How can we derive prediction sets that are optimal for such decision makers? We provide an exact characterization in the population regime and a distribution free finite-sample construction. Answering these questions naturally leads to an algorithm, Risk-Averse Calibration (RAC), which follows a provably optimal design for deriving action policies from predictions. RAC is designed to be both practical-capable of leveraging the quality of predictions in a black-box manner to enhance downstream utility-and safe-adhering to a user-defined risk threshold and optimizing the corresponding risk quantile of the user's downstream utility. Finally, we experimentally demonstrate the significant advantages of RAC in applications such as medical diagnosis and recommendation systems. Specifically, we show that RAC achieves a substantially improved trade-off between safety and utility, offering higher utility compared to existing methods while maintaining the safety guarantee.

Adversarial Reasoning at Jailbreaking Time

As large language models (LLMs) are becoming more capable and widespread, the study of their failure cases is becoming increasingly important. Recent advances in standardizing, measuring, and scaling test-time compute suggest new methodologies for optimizing models to achieve high performance on hard tasks. In this paper, we apply these advances to the task of model jailbreaking: eliciting harmful responses from aligned LLMs. We develop an adversarial reasoning approach to automatic jailbreaking via test-time computation that achieves SOTA attack success rates (ASR) against many aligned LLMs, even the ones that aim to trade inference-time compute for adversarial robustness. Our approach introduces a new paradigm in understanding LLM vulnerabilities, laying the foundation for the development of more robust and trustworthy AI systems.

Symmetries-enhanced Multi-Agent Reinforcement Learning

Multi-agent reinforcement learning has emerged as a powerful framework for enabling agents to learn complex, coordinated behaviors but faces persistent challenges regarding its generalization, scalability and sample efficiency. Recent advancements have sought to alleviate those issues by embedding intrinsic symmetries of the systems in the policy. Yet, most dynamical systems exhibit little to no symmetries to exploit. This paper presents a novel framework for embedding extrinsic symmetries in multi-agent system dynamics that enables the use of symmetry-enhanced methods to address systems with insufficient intrinsic symmetries, expanding the scope of equivariant learning to a wide variety of MARL problems. Central to our framework is the Group Equivariant Graphormer, a group-modular architecture specifically designed for distributed swarming tasks. Extensive experiments on a swarm of symmetry-breaking quadrotors validate the effectiveness of our approach, showcasing its potential for improved generalization and zero-shot scalability. Our method achieves significant reductions in collision rates and enhances task success rates across a diverse range of scenarios and varying swarm sizes.

STLGame: Signal Temporal Logic Games in Adversarial Multi-Agent Systems

We study how to synthesize a robust and safe policy for autonomous systems under signal temporal logic (STL) tasks in adversarial settings against unknown dynamic agents. To ensure the worst-case STL satisfaction, we propose STLGame, a framework that models the multi-agent system as a two-player zero-sum game, where the ego agents try to maximize the STL satisfaction and other agents minimize it. STLGame aims to find a Nash equilibrium policy profile, which is the best case in terms of robustness against unseen opponent policies, by using the fictitious self-play (FSP) framework. FSP iteratively converges to a Nash profile, even in games set in continuous state-action spaces. We propose a gradient-based method with differentiable STL formulas, which is crucial in continuous settings to approximate the best responses at each iteration of FSP. We show this key aspect experimentally by comparing with reinforcement learning-based methods to find the best response. Experiments on two standard dynamical system benchmarks, Ackermann steering vehicles and autonomous drones, demonstrate that our converged policy is almost unexploitable and robust to various unseen opponents' policies. All code and additional experimental results can be found on our project website: https://sites.google.com/view/stlgame

Length Optimization in Conformal Prediction

Conditional validity and length efficiency are two crucial aspects of conformal prediction (CP). Achieving conditional validity ensures accurate uncertainty quantification for data subpopulations, while proper length efficiency ensures that the prediction sets remain informative and non-trivial. Despite significant efforts to address each of these issues individually, a principled framework that reconciles these two objectives has been missing in the CP literature. In this paper, we develop Conformal Prediction with Length-Optimization (CPL) - a novel framework that constructs prediction sets with (near-) optimal length while ensuring conditional validity under various classes of covariate shifts, including the key cases of marginal and group-conditional coverage. In the infinite sample regime, we provide strong duality results which indicate that CPL achieves conditional validity and length optimality. In the finite sample regime, we show that CPL constructs conditionally valid prediction sets. Our extensive empirical evaluations demonstrate the superior prediction set size performance of CPL compared to state-of-the-art methods across diverse real-world and synthetic datasets in classification, regression, and text-related settings.