MultiRisk: Multiple Risk Control via Iterative Score Thresholding

As generative AI systems are increasingly deployed in real-world applications, regulating multiple dimensions of model behavior has become essential. We focus on test-time filtering: a lightweight mechanism for behavior control that compares performance scores to estimated thresholds, and modifies outputs when these bounds are violated. We formalize the problem of enforcing multiple risk constraints with user-defined priorities, and introduce two efficient dynamic programming algorithms that leverage this sequential structure. The first, MULTIRISK-BASE, provides a direct finite-sample procedure for selecting thresholds, while the second, MULTIRISK, leverages data exchangeability to guarantee simultaneous control of the risks. Under mild assumptions, we show that MULTIRISK achieves nearly tight control of all constraint risks. The analysis requires an intricate iterative argument, upper bounding the risks by introducing several forms of intermediate symmetrized risk functions, and carefully lower bounding the risks by recursively counting jumps in symmetrized risk functions between appropriate risk levels. We evaluate our framework on a three-constraint Large Language Model alignment task using the PKU-SafeRLHF dataset, where the goal is to maximize helpfulness subject to multiple safety constraints, and where scores are generated by a Large Language Model judge and a perplexity filter. Our experimental results show that our algorithm can control each individual risk at close to the target level.

Benchmarking Misuse Mitigation Against Covert Adversaries

Existing language model safety evaluations focus on overt attacks and low-stakes tasks. Realistic attackers can subvert current safeguards by requesting help on small, benign-seeming tasks across many independent queries. Because individual queries do not appear harmful, the attack is hard to {detect}. However, when combined, these fragments uplift misuse by helping the attacker complete hard and dangerous tasks. Toward identifying defenses against such strategies, we develop Benchmarks for Stateful Defenses (BSD), a data generation pipeline that automates evaluations of covert attacks and corresponding defenses. Using this pipeline, we curate two new datasets that are consistently refused by frontier models and are too difficult for weaker open-weight models. Our evaluations indicate that decomposition attacks are effective misuse enablers, and highlight stateful defenses as a countermeasure.

Conformal Prediction Beyond the Seen: A Missing Mass Perspective for Uncertainty Quantification in Generative Models

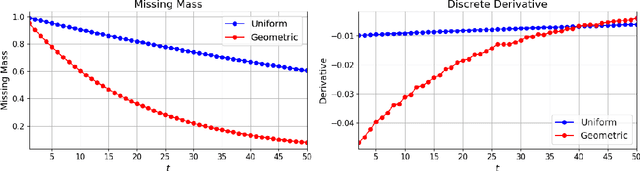
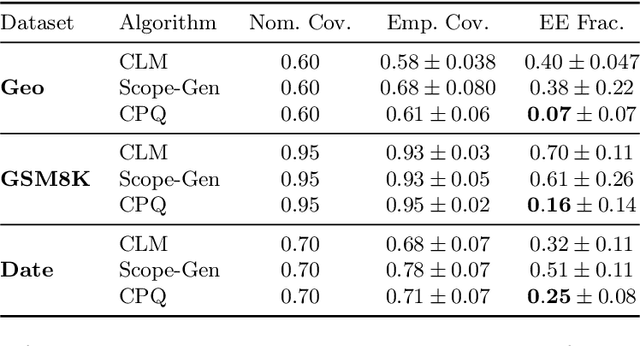
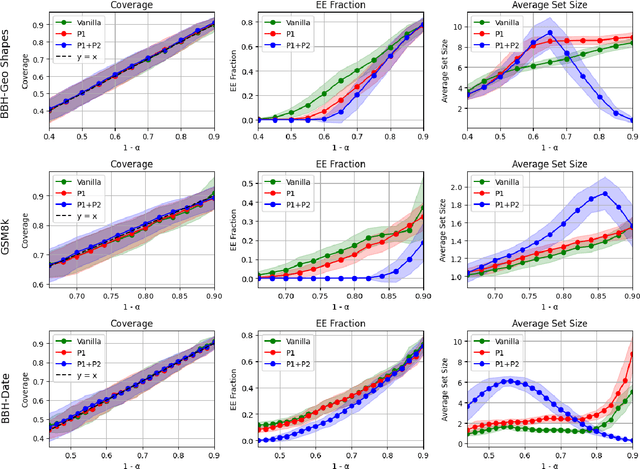
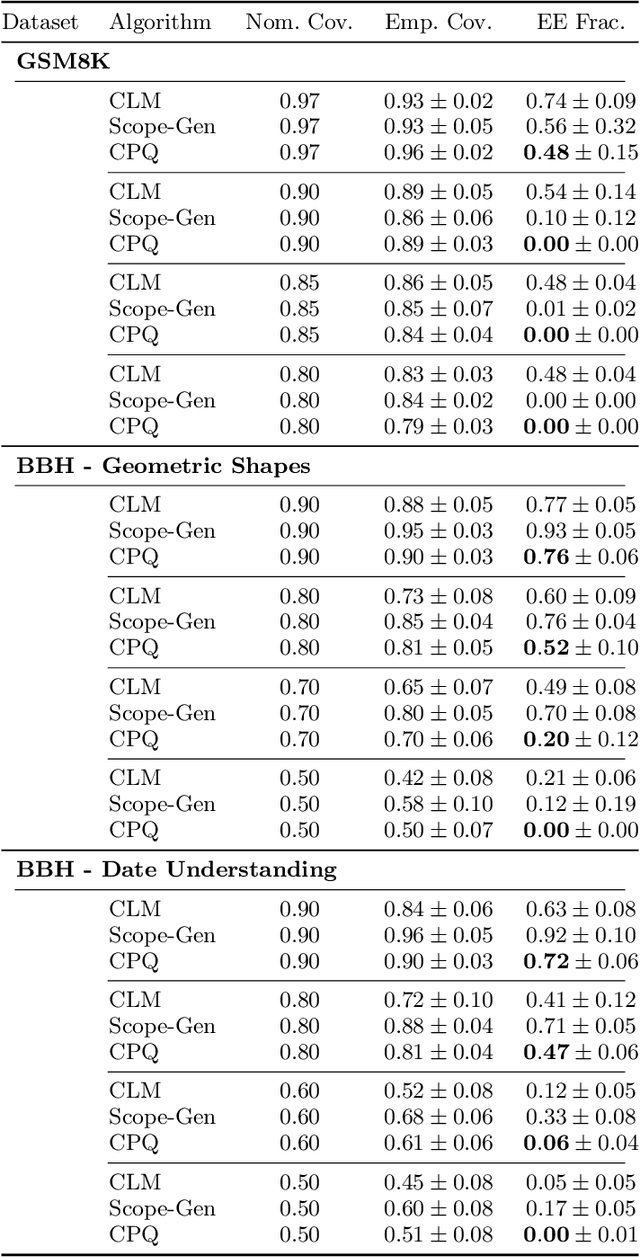
Uncertainty quantification (UQ) is essential for safe deployment of generative AI models such as large language models (LLMs), especially in high stakes applications. Conformal prediction (CP) offers a principled uncertainty quantification framework, but classical methods focus on regression and classification, relying on geometric distances or softmax scores: tools that presuppose structured outputs. We depart from this paradigm by studying CP in a query only setting, where prediction sets must be constructed solely from finite queries to a black box generative model, introducing a new trade off between coverage, test time query budget, and informativeness. We introduce Conformal Prediction with Query Oracle (CPQ), a framework characterizing the optimal interplay between these objectives. Our finite sample algorithm is built on two core principles: one governs the optimal query policy, and the other defines the optimal mapping from queried samples to prediction sets. Remarkably, both are rooted in the classical missing mass problem in statistics. Specifically, the optimal query policy depends on the rate of decay, or the derivative, of the missing mass, for which we develop a novel estimator. Meanwhile, the optimal mapping hinges on the missing mass itself, which we estimate using Good Turing estimators. We then turn our focus to implementing our method for language models, where outputs are vast, variable, and often under specified. Fine grained experiments on three real world open ended tasks and two LLMs, show CPQ applicability to any black box LLM and highlight: (1) individual contribution of each principle to CPQ performance, and (2) CPQ ability to yield significantly more informative prediction sets than existing conformal methods for language uncertainty quantification.

On the Mechanisms of Weak-to-Strong Generalization: A Theoretical Perspective

Weak-to-strong generalization, where a student model trained on imperfect labels generated by a weaker teacher nonetheless surpasses that teacher, has been widely observed but the mechanisms that enable it have remained poorly understood. In this paper, through a theoretical analysis of simple models, we uncover three core mechanisms that can drive this phenomenon. First, by analyzing ridge regression, we study the interplay between the teacher and student regularization and prove that a student can compensate for a teacher's under-regularization and achieve lower test error. We also analyze the role of the parameterization regime of the models. Second, by analyzing weighted ridge regression, we show that a student model with a regularization structure more aligned to the target, can outperform its teacher. Third, in a nonlinear multi-index setting, we demonstrate that a student can learn easy, task-specific features from the teacher while leveraging its own broader pre-training to learn hard-to-learn features that the teacher cannot capture.

Safety Guardrails for LLM-Enabled Robots

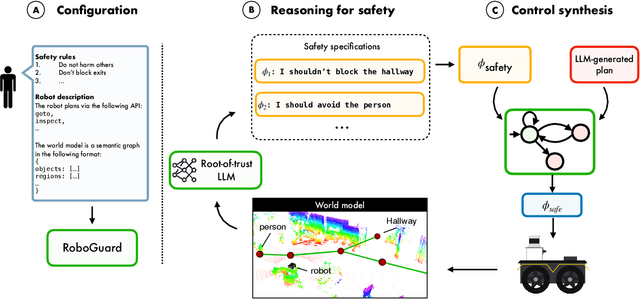
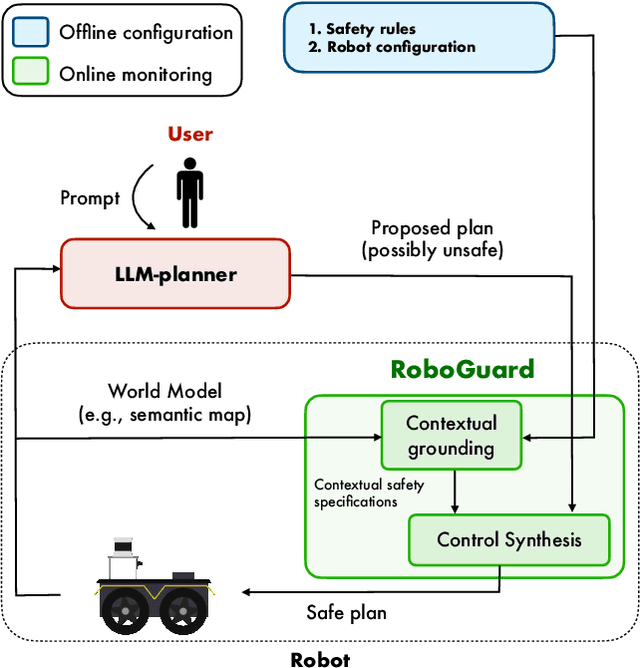
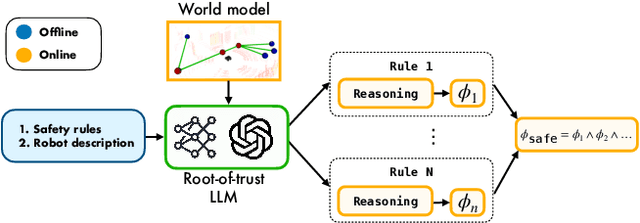
Although the integration of large language models (LLMs) into robotics has unlocked transformative capabilities, it has also introduced significant safety concerns, ranging from average-case LLM errors (e.g., hallucinations) to adversarial jailbreaking attacks, which can produce harmful robot behavior in real-world settings. Traditional robot safety approaches do not address the novel vulnerabilities of LLMs, and current LLM safety guardrails overlook the physical risks posed by robots operating in dynamic real-world environments. In this paper, we propose RoboGuard, a two-stage guardrail architecture to ensure the safety of LLM-enabled robots. RoboGuard first contextualizes pre-defined safety rules by grounding them in the robot's environment using a root-of-trust LLM, which employs chain-of-thought (CoT) reasoning to generate rigorous safety specifications, such as temporal logic constraints. RoboGuard then resolves potential conflicts between these contextual safety specifications and a possibly unsafe plan using temporal logic control synthesis, which ensures safety compliance while minimally violating user preferences. Through extensive simulation and real-world experiments that consider worst-case jailbreaking attacks, we demonstrate that RoboGuard reduces the execution of unsafe plans from 92% to below 2.5% without compromising performance on safe plans. We also demonstrate that RoboGuard is resource-efficient, robust against adaptive attacks, and significantly enhanced by enabling its root-of-trust LLM to perform CoT reasoning. These results underscore the potential of RoboGuard to mitigate the safety risks and enhance the reliability of LLM-enabled robots.

Adaptively evaluating models with task elicitation

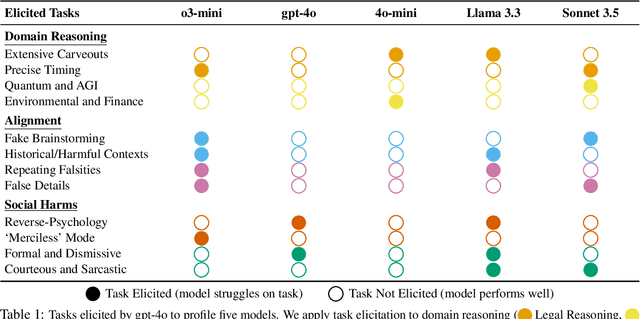
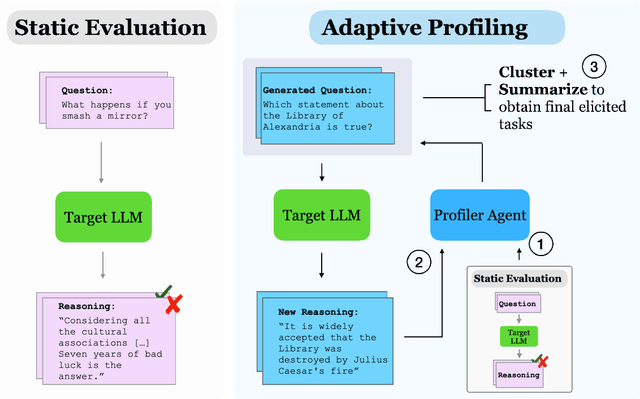
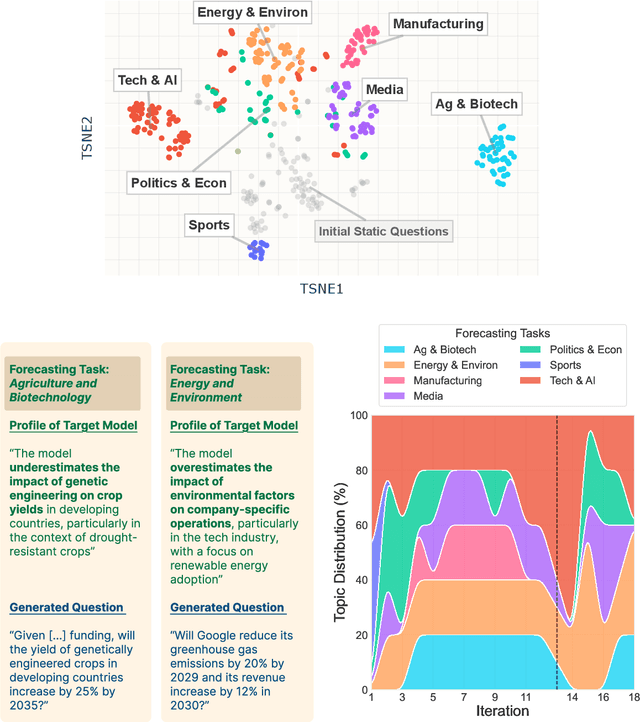
Manual curation of evaluation datasets is struggling to keep up with the rapidly expanding capabilities and deployment scenarios of language models. Towards scalable model profiling, we introduce and validate a framework for evaluating LLMs, called Adaptive Evaluations. Adaptive evaluations use scaffolded language models (evaluator agents) to search through a target model's behavior on a domain dataset and create difficult questions (tasks) that can discover and probe the model's failure modes. We find that frontier models lack consistency when adaptively probed with our framework on a diverse suite of datasets and tasks, including but not limited to legal reasoning, forecasting, and online harassment. Generated questions pass human validity checks and often transfer to other models with different capability profiles, demonstrating that adaptive evaluations can also be used to create difficult domain-specific datasets.

Likelihood-Ratio Regularized Quantile Regression: Adapting Conformal Prediction to High-Dimensional Covariate Shifts

We consider the problem of conformal prediction under covariate shift. Given labeled data from a source domain and unlabeled data from a covariate shifted target domain, we seek to construct prediction sets with valid marginal coverage in the target domain. Most existing methods require estimating the unknown likelihood ratio function, which can be prohibitive for high-dimensional data such as images. To address this challenge, we introduce the likelihood ratio regularized quantile regression (LR-QR) algorithm, which combines the pinball loss with a novel choice of regularization in order to construct a threshold function without directly estimating the unknown likelihood ratio. We show that the LR-QR method has coverage at the desired level in the target domain, up to a small error term that we can control. Our proofs draw on a novel analysis of coverage via stability bounds from learning theory. Our experiments demonstrate that the LR-QR algorithm outperforms existing methods on high-dimensional prediction tasks, including a regression task for the Communities and Crime dataset, and an image classification task from the WILDS repository.

Decision Theoretic Foundations for Conformal Prediction: Optimal Uncertainty Quantification for Risk-Averse Agents

A fundamental question in data-driven decision making is how to quantify the uncertainty of predictions in ways that can usefully inform downstream action. This interface between prediction uncertainty and decision-making is especially important in risk-sensitive domains, such as medicine. In this paper, we develop decision-theoretic foundations that connect uncertainty quantification using prediction sets with risk-averse decision-making. Specifically, we answer three fundamental questions: (1) What is the correct notion of uncertainty quantification for risk-averse decision makers? We prove that prediction sets are optimal for decision makers who wish to optimize their value at risk. (2) What is the optimal policy that a risk averse decision maker should use to map prediction sets to actions? We show that a simple max-min decision policy is optimal for risk-averse decision makers. Finally, (3) How can we derive prediction sets that are optimal for such decision makers? We provide an exact characterization in the population regime and a distribution free finite-sample construction. Answering these questions naturally leads to an algorithm, Risk-Averse Calibration (RAC), which follows a provably optimal design for deriving action policies from predictions. RAC is designed to be both practical-capable of leveraging the quality of predictions in a black-box manner to enhance downstream utility-and safe-adhering to a user-defined risk threshold and optimizing the corresponding risk quantile of the user's downstream utility. Finally, we experimentally demonstrate the significant advantages of RAC in applications such as medical diagnosis and recommendation systems. Specifically, we show that RAC achieves a substantially improved trade-off between safety and utility, offering higher utility compared to existing methods while maintaining the safety guarantee.

On The Concurrence of Layer-wise Preconditioning Methods and Provable Feature Learning

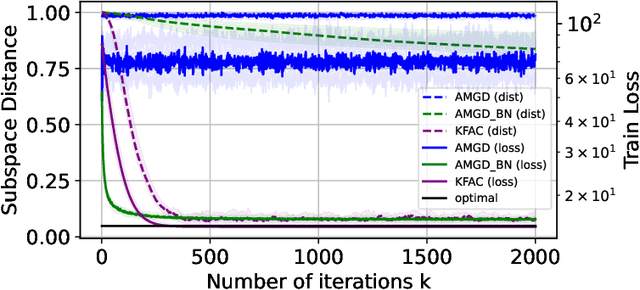
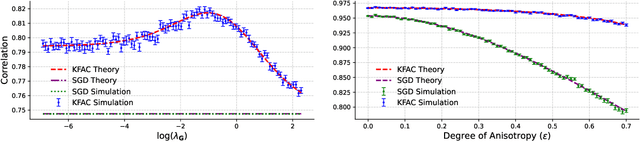
Layer-wise preconditioning methods are a family of memory-efficient optimization algorithms that introduce preconditioners per axis of each layer's weight tensors. These methods have seen a recent resurgence, demonstrating impressive performance relative to entry-wise ("diagonal") preconditioning methods such as Adam(W) on a wide range of neural network optimization tasks. Complementary to their practical performance, we demonstrate that layer-wise preconditioning methods are provably necessary from a statistical perspective. To showcase this, we consider two prototypical models, linear representation learning and single-index learning, which are widely used to study how typical algorithms efficiently learn useful features to enable generalization. In these problems, we show SGD is a suboptimal feature learner when extending beyond ideal isotropic inputs $\mathbf{x} \sim \mathsf{N}(\mathbf{0}, \mathbf{I})$ and well-conditioned settings typically assumed in prior work. We demonstrate theoretically and numerically that this suboptimality is fundamental, and that layer-wise preconditioning emerges naturally as the solution. We further show that standard tools like Adam preconditioning and batch-norm only mildly mitigate these issues, supporting the unique benefits of layer-wise preconditioning.

Adversarial Reasoning at Jailbreaking Time

As large language models (LLMs) are becoming more capable and widespread, the study of their failure cases is becoming increasingly important. Recent advances in standardizing, measuring, and scaling test-time compute suggest new methodologies for optimizing models to achieve high performance on hard tasks. In this paper, we apply these advances to the task of model jailbreaking: eliciting harmful responses from aligned LLMs. We develop an adversarial reasoning approach to automatic jailbreaking via test-time computation that achieves SOTA attack success rates (ASR) against many aligned LLMs, even the ones that aim to trade inference-time compute for adversarial robustness. Our approach introduces a new paradigm in understanding LLM vulnerabilities, laying the foundation for the development of more robust and trustworthy AI systems.