On The Concurrence of Layer-wise Preconditioning Methods and Provable Feature Learning

Layer-wise preconditioning methods are a family of memory-efficient optimization algorithms that introduce preconditioners per axis of each layer's weight tensors. These methods have seen a recent resurgence, demonstrating impressive performance relative to entry-wise ("diagonal") preconditioning methods such as Adam(W) on a wide range of neural network optimization tasks. Complementary to their practical performance, we demonstrate that layer-wise preconditioning methods are provably necessary from a statistical perspective. To showcase this, we consider two prototypical models, linear representation learning and single-index learning, which are widely used to study how typical algorithms efficiently learn useful features to enable generalization. In these problems, we show SGD is a suboptimal feature learner when extending beyond ideal isotropic inputs $\mathbf{x} \sim \mathsf{N}(\mathbf{0}, \mathbf{I})$ and well-conditioned settings typically assumed in prior work. We demonstrate theoretically and numerically that this suboptimality is fundamental, and that layer-wise preconditioning emerges naturally as the solution. We further show that standard tools like Adam preconditioning and batch-norm only mildly mitigate these issues, supporting the unique benefits of layer-wise preconditioning.

Asymptotics of Linear Regression with Linearly Dependent Data

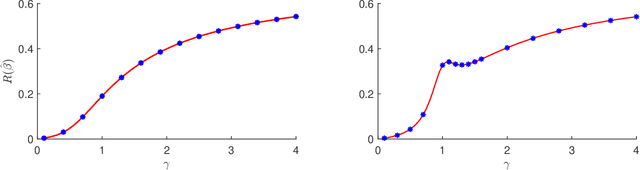
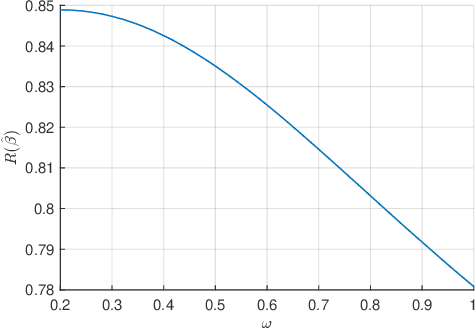
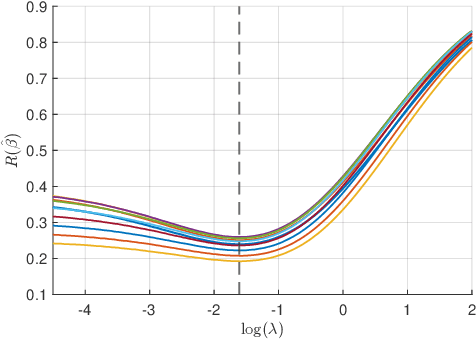
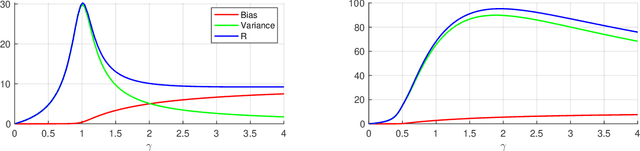
In this paper we study the asymptotics of linear regression in settings where the covariates exhibit a linear dependency structure, departing from the standard assumption of independence. We model the covariates using stochastic processes with spatio-temporal covariance and analyze the performance of ridge regression in the high-dimensional proportional regime, where the number of samples and feature dimensions grow proportionally. A Gaussian universality theorem is proven, demonstrating that the asymptotics are invariant under replacing the covariates with Gaussian vectors preserving mean and covariance. Next, leveraging tools from random matrix theory, we derive precise characterizations of the estimation error. The estimation error is characterized by a fixed-point equation involving the spectral properties of the spatio-temporal covariance matrices, enabling efficient computation. We then study optimal regularization, overparameterization, and the double descent phenomenon in the context of dependent data. Simulations validate our theoretical predictions, shedding light on how dependencies influence estimation error and the choice of regularization parameters.

Signal-Plus-Noise Decomposition of Nonlinear Spiked Random Matrix Models

In this paper, we study a nonlinear spiked random matrix model where a nonlinear function is applied element-wise to a noise matrix perturbed by a rank-one signal. We establish a signal-plus-noise decomposition for this model and identify precise phase transitions in the structure of the signal components at critical thresholds of signal strength. To demonstrate the applicability of this decomposition, we then utilize it to study new phenomena in the problems of signed signal recovery in nonlinear models and community detection in transformed stochastic block models. Finally, we validate our results through a series of numerical simulations.

A Theory of Non-Linear Feature Learning with One Gradient Step in Two-Layer Neural Networks

Feature learning is thought to be one of the fundamental reasons for the success of deep neural networks. It is rigorously known that in two-layer fully-connected neural networks under certain conditions, one step of gradient descent on the first layer followed by ridge regression on the second layer can lead to feature learning; characterized by the appearance of a separated rank-one component -- spike -- in the spectrum of the feature matrix. However, with a constant gradient descent step size, this spike only carries information from the linear component of the target function and therefore learning non-linear components is impossible. We show that with a learning rate that grows with the sample size, such training in fact introduces multiple rank-one components, each corresponding to a specific polynomial feature. We further prove that the limiting large-dimensional and large sample training and test errors of the updated neural networks are fully characterized by these spikes. By precisely analyzing the improvement in the loss, we demonstrate that these non-linear features can enhance learning.

Demystifying Disagreement-on-the-Line in High Dimensions

Evaluating the performance of machine learning models under distribution shift is challenging, especially when we only have unlabeled data from the shifted (target) domain, along with labeled data from the original (source) domain. Recent work suggests that the notion of disagreement, the degree to which two models trained with different randomness differ on the same input, is a key to tackle this problem. Experimentally, disagreement and prediction error have been shown to be strongly connected, which has been used to estimate model performance. Experiments have lead to the discovery of the disagreement-on-the-line phenomenon, whereby the classification error under the target domain is often a linear function of the classification error under the source domain; and whenever this property holds, disagreement under the source and target domain follow the same linear relation. In this work, we develop a theoretical foundation for analyzing disagreement in high-dimensional random features regression; and study under what conditions the disagreement-on-the-line phenomenon occurs in our setting. Experiments on CIFAR-10-C, Tiny ImageNet-C, and Camelyon17 are consistent with our theory and support the universality of the theoretical findings.

Information-Theoretic Analysis of Minimax Excess Risk

Two main concepts studied in machine learning theory are generalization gap (difference between train and test error) and excess risk (difference between test error and the minimum possible error). While information-theoretic tools have been used extensively to study the generalization gap of learning algorithms, the information-theoretic nature of excess risk has not yet been fully investigated. In this paper, some steps are taken toward this goal. We consider the frequentist problem of minimax excess risk as a zero-sum game between algorithm designer and the world. Then, we argue that it is desirable to modify this game in a way that the order of play can be swapped. We prove that, under some regularity conditions, if the world and designer can play randomly the duality gap is zero and the order of play can be changed. In this case, a Bayesian problem surfaces in the dual representation. This makes it possible to utilize recent information-theoretic results on minimum excess risk in Bayesian learning to provide bounds on the minimax excess risk. We demonstrate the applicability of the results by providing information theoretic insight on two important classes of problems: classification when the hypothesis space has finite VC-dimension, and regularized least squares.

Rate-Distortion Analysis of Minimum Excess Risk in Bayesian Learning

Minimum Excess Risk (MER) in Bayesian learning is defined as the difference between the minimum expected loss achievable when learning from data and the minimum expected loss that could be achieved if the underlying parameter $W$ was observed. In this paper, we build upon and extend the recent results of (Xu & Raginsky, 2020) to analyze the MER in Bayesian learning and derive information-theoretic bounds on it. We formulate the problem as a (constrained) rate-distortion optimization and show how the solution can be bounded above and below by two other rate-distortion functions that are easier to study. The lower bound represents the minimum possible excess risk achievable by \emph{any} process using $R$ bits of information from the parameter $W$. For the upper bound, the optimization is further constrained to use $R$ bits from the training set, a setting which relates MER to information-theoretic bounds on the generalization gap in frequentist learning. We derive information-theoretic bounds on the difference between these upper and lower bounds and show that they can provide order-wise tight rates for MER. This analysis gives more insight into the information-theoretic nature of Bayesian learning as well as providing novel bounds.