SPARKLE: A Unified Single-Loop Primal-Dual Framework for Decentralized Bilevel Optimization

This paper studies decentralized bilevel optimization, in which multiple agents collaborate to solve problems involving nested optimization structures with neighborhood communications. Most existing literature primarily utilizes gradient tracking to mitigate the influence of data heterogeneity, without exploring other well-known heterogeneity-correction techniques such as EXTRA or Exact Diffusion. Additionally, these studies often employ identical decentralized strategies for both upper- and lower-level problems, neglecting to leverage distinct mechanisms across different levels. To address these limitations, this paper proposes SPARKLE, a unified Single-loop Primal-dual AlgoRithm frameworK for decentraLized bilEvel optimization. SPARKLE offers the flexibility to incorporate various heterogeneitycorrection strategies into the algorithm. Moreover, SPARKLE allows for different strategies to solve upper- and lower-level problems. We present a unified convergence analysis for SPARKLE, applicable to all its variants, with state-of-the-art convergence rates compared to existing decentralized bilevel algorithms. Our results further reveal that EXTRA and Exact Diffusion are more suitable for decentralized bilevel optimization, and using mixed strategies in bilevel algorithms brings more benefits than relying solely on gradient tracking.

One-Shot Safety Alignment for Large Language Models via Optimal Dualization

The growing safety concerns surrounding Large Language Models (LLMs) raise an urgent need to align them with diverse human preferences to simultaneously enhance their helpfulness and safety. A promising approach is to enforce safety constraints through Reinforcement Learning from Human Feedback (RLHF). For such constrained RLHF, common Lagrangian-based primal-dual policy optimization methods are computationally expensive and often unstable. This paper presents a dualization perspective that reduces constrained alignment to an equivalent unconstrained alignment problem. We do so by pre-optimizing a smooth and convex dual function that has a closed form. This shortcut eliminates the need for cumbersome primal-dual policy iterations, thus greatly reducing the computational burden and improving training stability. Our strategy leads to two practical algorithms in model-based and preference-based scenarios (MoCAN and PeCAN, respectively). A broad range of experiments demonstrate the effectiveness of our methods.

Uncertainty in Language Models: Assessment through Rank-Calibration

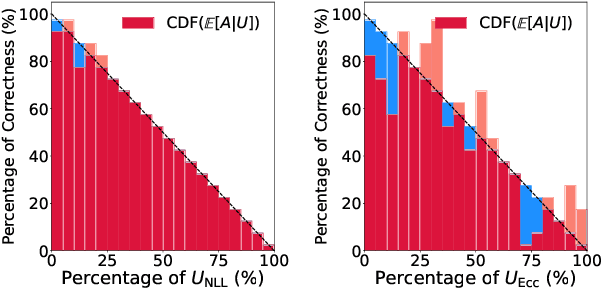
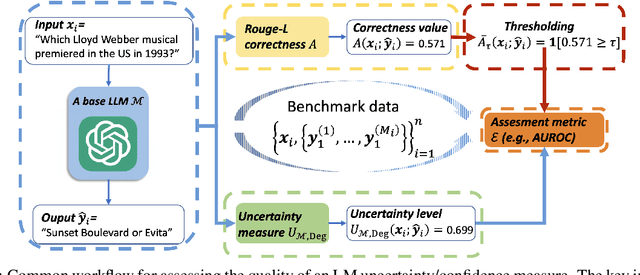
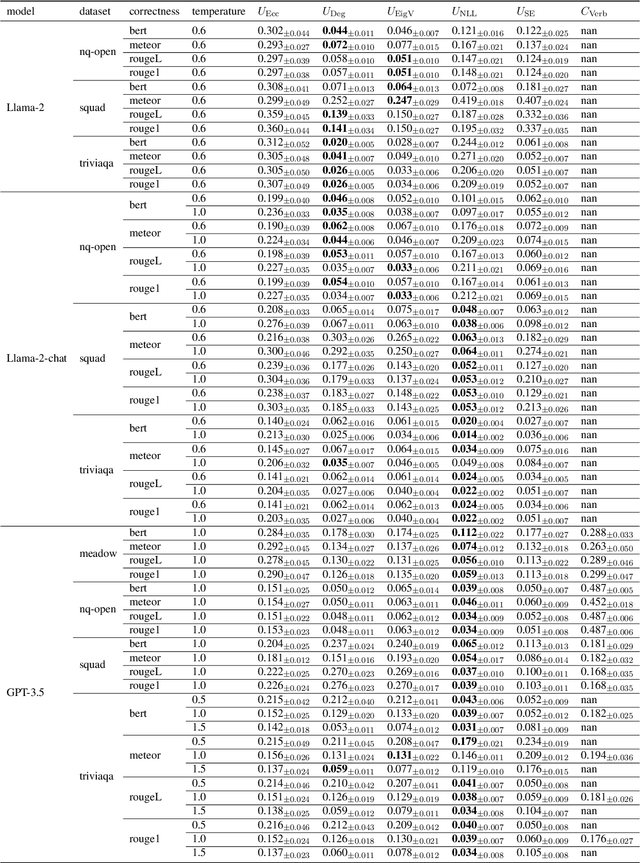
Language Models (LMs) have shown promising performance in natural language generation. However, as LMs often generate incorrect or hallucinated responses, it is crucial to correctly quantify their uncertainty in responding to given inputs. In addition to verbalized confidence elicited via prompting, many uncertainty measures ($e.g.$, semantic entropy and affinity-graph-based measures) have been proposed. However, these measures can differ greatly, and it is unclear how to compare them, partly because they take values over different ranges ($e.g.$, $[0,\infty)$ or $[0,1]$). In this work, we address this issue by developing a novel and practical framework, termed $Rank$-$Calibration$, to assess uncertainty and confidence measures for LMs. Our key tenet is that higher uncertainty (or lower confidence) should imply lower generation quality, on average. Rank-calibration quantifies deviations from this ideal relationship in a principled manner, without requiring ad hoc binary thresholding of the correctness score ($e.g.$, ROUGE or METEOR). The broad applicability and the granular interpretability of our methods are demonstrated empirically.

Decentralized Bilevel Optimization over Graphs: Loopless Algorithmic Update and Transient Iteration Complexity

Stochastic bilevel optimization (SBO) is becoming increasingly essential in machine learning due to its versatility in handling nested structures. To address large-scale SBO, decentralized approaches have emerged as effective paradigms in which nodes communicate with immediate neighbors without a central server, thereby improving communication efficiency and enhancing algorithmic robustness. However, current decentralized SBO algorithms face challenges, including expensive inner-loop updates and unclear understanding of the influence of network topology, data heterogeneity, and the nested bilevel algorithmic structures. In this paper, we introduce a single-loop decentralized SBO (D-SOBA) algorithm and establish its transient iteration complexity, which, for the first time, clarifies the joint influence of network topology and data heterogeneity on decentralized bilevel algorithms. D-SOBA achieves the state-of-the-art asymptotic rate, asymptotic gradient/Hessian complexity, and transient iteration complexity under more relaxed assumptions compared to existing methods. Numerical experiments validate our theoretical findings.

Stochastic Controlled Averaging for Federated Learning with Communication Compression

Communication compression, a technique aiming to reduce the information volume to be transmitted over the air, has gained great interests in Federated Learning (FL) for the potential of alleviating its communication overhead. However, communication compression brings forth new challenges in FL due to the interplay of compression-incurred information distortion and inherent characteristics of FL such as partial participation and data heterogeneity. Despite the recent development, the performance of compressed FL approaches has not been fully exploited. The existing approaches either cannot accommodate arbitrary data heterogeneity or partial participation, or require stringent conditions on compression. In this paper, we revisit the seminal stochastic controlled averaging method by proposing an equivalent but more efficient/simplified formulation with halved uplink communication costs. Building upon this implementation, we propose two compressed FL algorithms, SCALLION and SCAFCOM, to support unbiased and biased compression, respectively. Both the proposed methods outperform the existing compressed FL methods in terms of communication and computation complexities. Moreover, SCALLION and SCAFCOM accommodates arbitrary data heterogeneity and do not make any additional assumptions on compression errors. Experiments show that SCALLION and SCAFCOM can match the performance of corresponding full-precision FL approaches with substantially reduced uplink communication, and outperform recent compressed FL methods under the same communication budget.

Momentum Benefits Non-IID Federated Learning Simply and Provably

Federated learning is a powerful paradigm for large-scale machine learning, but it faces significant challenges due to unreliable network connections, slow communication, and substantial data heterogeneity across clients. FedAvg and SCAFFOLD are two fundamental algorithms to address these challenges. In particular, FedAvg employs multiple local updates before communicating with a central server, while SCAFFOLD maintains a control variable on each client to compensate for "client drift" in its local updates. Various methods have been proposed in literature to enhance the convergence of these two algorithms, but they either make impractical adjustments to algorithmic structure, or rely on the assumption of bounded data heterogeneity. This paper explores the utilization of momentum to enhance the performance of FedAvg and SCAFFOLD. When all clients participate in the training process, we demonstrate that incorporating momentum allows FedAvg to converge without relying on the assumption of bounded data heterogeneity even using a constant local learning rate. This is a novel result since existing analyses for FedAvg require bounded data heterogeneity even with diminishing local learning rates. In the case of partial client participation, we show that momentum enables SCAFFOLD to converge provably faster without imposing any additional assumptions. Furthermore, we use momentum to develop new variance-reduced extensions of FedAvg and SCAFFOLD, which exhibit state-of-the-art convergence rates. Our experimental results support all theoretical findings.

Optimal Heterogeneous Collaborative Linear Regression and Contextual Bandits

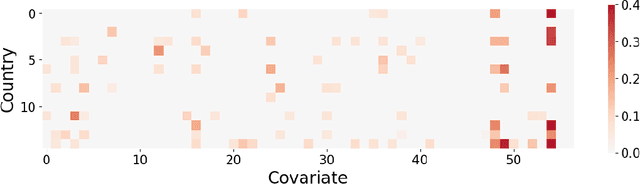
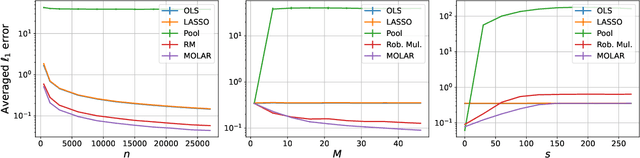
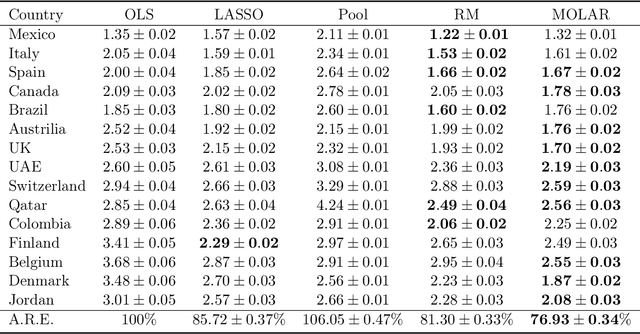
Large and complex datasets are often collected from several, possibly heterogeneous sources. Collaborative learning methods improve efficiency by leveraging commonalities across datasets while accounting for possible differences among them. Here we study collaborative linear regression and contextual bandits, where each instance's associated parameters are equal to a global parameter plus a sparse instance-specific term. We propose a novel two-stage estimator called MOLAR that leverages this structure by first constructing an entry-wise median of the instances' linear regression estimates, and then shrinking the instance-specific estimates towards the median. MOLAR improves the dependence of the estimation error on the data dimension, compared to independent least squares estimates. We then apply MOLAR to develop methods for sparsely heterogeneous collaborative contextual bandits, which lead to improved regret guarantees compared to independent bandit methods. We further show that our methods are minimax optimal by providing a number of lower bounds. Finally, we support the efficiency of our methods by performing experiments on both synthetic data and the PISA dataset on student educational outcomes from heterogeneous countries.

Unbiased Compression Saves Communication in Distributed Optimization: When and How Much?

Communication compression is a common technique in distributed optimization that can alleviate communication overhead by transmitting compressed gradients and model parameters. However, compression can introduce information distortion, which slows down convergence and incurs more communication rounds to achieve desired solutions. Given the trade-off between lower per-round communication costs and additional rounds of communication, it is unclear whether communication compression reduces the total communication cost. This paper explores the conditions under which unbiased compression, a widely used form of compression, can reduce the total communication cost, as well as the extent to which it can do so. To this end, we present the first theoretical formulation for characterizing the total communication cost in distributed optimization with communication compression. We demonstrate that unbiased compression alone does not necessarily save the total communication cost, but this outcome can be achieved if the compressors used by all workers are further assumed independent. We establish lower bounds on the communication rounds required by algorithms using independent unbiased compressors to minimize smooth convex functions, and show that these lower bounds are tight by refining the analysis for ADIANA. Our results reveal that using independent unbiased compression can reduce the total communication cost by a factor of up to $\Theta(\sqrt{\min\{n, \kappa\}})$, where $n$ is the number of workers and $\kappa$ is the condition number of the functions being minimized. These theoretical findings are supported by experimental results.

Lower Bounds and Accelerated Algorithms in Distributed Stochastic Optimization with Communication Compression

Communication compression is an essential strategy for alleviating communication overhead by reducing the volume of information exchanged between computing nodes in large-scale distributed stochastic optimization. Although numerous algorithms with convergence guarantees have been obtained, the optimal performance limit under communication compression remains unclear. In this paper, we investigate the performance limit of distributed stochastic optimization algorithms employing communication compression. We focus on two main types of compressors, unbiased and contractive, and address the best-possible convergence rates one can obtain with these compressors. We establish the lower bounds for the convergence rates of distributed stochastic optimization in six different settings, combining strongly-convex, generally-convex, or non-convex functions with unbiased or contractive compressor types. To bridge the gap between lower bounds and existing algorithms' rates, we propose NEOLITHIC, a nearly optimal algorithm with compression that achieves the established lower bounds up to logarithmic factors under mild conditions. Extensive experimental results support our theoretical findings. This work provides insights into the theoretical limitations of existing compressors and motivates further research into fundamentally new compressor properties.

Demystifying Disagreement-on-the-Line in High Dimensions

Evaluating the performance of machine learning models under distribution shift is challenging, especially when we only have unlabeled data from the shifted (target) domain, along with labeled data from the original (source) domain. Recent work suggests that the notion of disagreement, the degree to which two models trained with different randomness differ on the same input, is a key to tackle this problem. Experimentally, disagreement and prediction error have been shown to be strongly connected, which has been used to estimate model performance. Experiments have lead to the discovery of the disagreement-on-the-line phenomenon, whereby the classification error under the target domain is often a linear function of the classification error under the source domain; and whenever this property holds, disagreement under the source and target domain follow the same linear relation. In this work, we develop a theoretical foundation for analyzing disagreement in high-dimensional random features regression; and study under what conditions the disagreement-on-the-line phenomenon occurs in our setting. Experiments on CIFAR-10-C, Tiny ImageNet-C, and Camelyon17 are consistent with our theory and support the universality of the theoretical findings.