Composition and Alignment of Diffusion Models using Constrained Learning

Diffusion models have become prevalent in generative modeling due to their ability to sample from complex distributions. To improve the quality of generated samples and their compliance with user requirements, two commonly used methods are: (i) Alignment, which involves fine-tuning a diffusion model to align it with a reward; and (ii) Composition, which combines several pre-trained diffusion models, each emphasizing a desirable attribute in the generated outputs. However, trade-offs often arise when optimizing for multiple rewards or combining multiple models, as they can often represent competing properties. Existing methods cannot guarantee that the resulting model faithfully generates samples with all the desired properties. To address this gap, we propose a constrained optimization framework that unifies alignment and composition of diffusion models by enforcing that the aligned model satisfies reward constraints and/or remains close to (potentially multiple) pre-trained models. We provide a theoretical characterization of the solutions to the constrained alignment and composition problems and develop a Lagrangian-based primal-dual training algorithm to approximate these solutions. Empirically, we demonstrate the effectiveness and merits of our proposed approach in image generation, applying it to alignment and composition, and show that our aligned or composed model satisfies constraints effectively, and improves on the equally-weighted approach. Our implementation can be found at https://github.com/shervinkhalafi/constrained_comp_align.

Alignment of large language models with constrained learning

We study the problem of computing an optimal large language model (LLM) policy for a constrained alignment problem, where the goal is to maximize a primary reward objective while satisfying constraints on secondary utilities. Despite the popularity of Lagrangian-based LLM policy search in constrained alignment, iterative primal-dual methods often fail to converge, and non-iterative dual-based methods do not achieve optimality in the LLM parameter space. To address these challenges, we employ Lagrangian duality to develop an iterative dual-based alignment method that alternates between updating the LLM policy via Lagrangian maximization and updating the dual variable via dual descent. In theory, we characterize the primal-dual gap between the primal value in the distribution space and the dual value in the LLM parameter space. We further quantify the optimality gap of the learned LLM policies at near-optimal dual variables with respect to both the objective and the constraint functions. These results prove that dual-based alignment methods can find an optimal constrained LLM policy, up to an LLM parametrization gap. We demonstrate the effectiveness and merits of our approach through extensive experiments conducted on the PKU-SafeRLHF dataset.

Constrained Diffusion Models via Dual Training

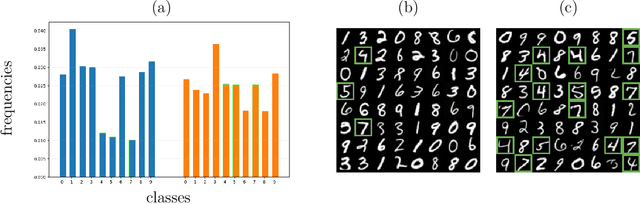
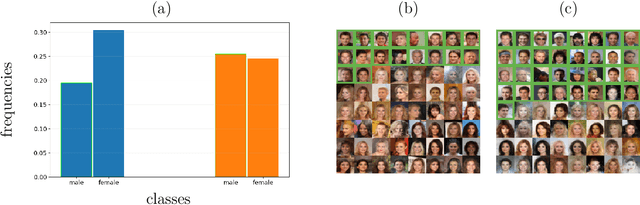
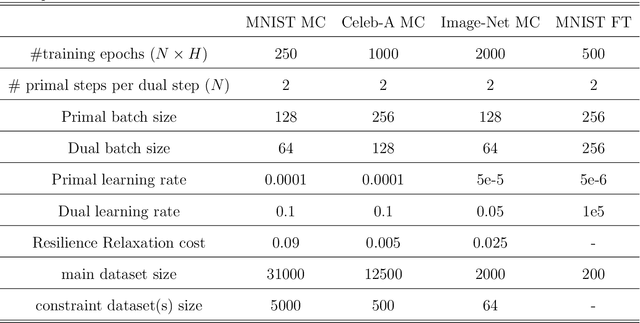
Diffusion models have attained prominence for their ability to synthesize a probability distribution for a given dataset via a diffusion process, enabling the generation of new data points with high fidelity. However, diffusion processes are prone to generating biased data based on the training dataset. To address this issue, we develop constrained diffusion models by imposing diffusion constraints based on desired distributions that are informed by requirements. Specifically, we cast the training of diffusion models under requirements as a constrained distribution optimization problem that aims to reduce the distribution difference between original and generated data while obeying constraints on the distribution of generated data. We show that our constrained diffusion models generate new data from a mixture data distribution that achieves the optimal trade-off among objective and constraints. To train constrained diffusion models, we develop a dual training algorithm and characterize the optimality of the trained constrained diffusion model. We empirically demonstrate the effectiveness of our constrained models in two constrained generation tasks: (i) we consider a dataset with one or more underrepresented classes where we train the model with constraints to ensure fairly sampling from all classes during inference; (ii) we fine-tune a pre-trained diffusion model to sample from a new dataset while avoiding overfitting.

Deterministic Policy Gradient Primal-Dual Methods for Continuous-Space Constrained MDPs

We study the problem of computing deterministic optimal policies for constrained Markov decision processes (MDPs) with continuous state and action spaces, which are widely encountered in constrained dynamical systems. Designing deterministic policy gradient methods in continuous state and action spaces is particularly challenging due to the lack of enumerable state-action pairs and the adoption of deterministic policies, hindering the application of existing policy gradient methods for constrained MDPs. To this end, we develop a deterministic policy gradient primal-dual method to find an optimal deterministic policy with non-asymptotic convergence. Specifically, we leverage regularization of the Lagrangian of the constrained MDP to propose a deterministic policy gradient primal-dual (D-PGPD) algorithm that updates the deterministic policy via a quadratic-regularized gradient ascent step and the dual variable via a quadratic-regularized gradient descent step. We prove that the primal-dual iterates of D-PGPD converge at a sub-linear rate to an optimal regularized primal-dual pair. We instantiate D-PGPD with function approximation and prove that the primal-dual iterates of D-PGPD converge at a sub-linear rate to an optimal regularized primal-dual pair, up to a function approximation error. Furthermore, we demonstrate the effectiveness of our method in two continuous control problems: robot navigation and fluid control. To the best of our knowledge, this appears to be the first work that proposes a deterministic policy search method for continuous-space constrained MDPs.

One-Shot Safety Alignment for Large Language Models via Optimal Dualization

The growing safety concerns surrounding Large Language Models (LLMs) raise an urgent need to align them with diverse human preferences to simultaneously enhance their helpfulness and safety. A promising approach is to enforce safety constraints through Reinforcement Learning from Human Feedback (RLHF). For such constrained RLHF, common Lagrangian-based primal-dual policy optimization methods are computationally expensive and often unstable. This paper presents a dualization perspective that reduces constrained alignment to an equivalent unconstrained alignment problem. We do so by pre-optimizing a smooth and convex dual function that has a closed form. This shortcut eliminates the need for cumbersome primal-dual policy iterations, thus greatly reducing the computational burden and improving training stability. Our strategy leads to two practical algorithms in model-based and preference-based scenarios (MoCAN and PeCAN, respectively). A broad range of experiments demonstrate the effectiveness of our methods.

Resilient Constrained Reinforcement Learning

We study a class of constrained reinforcement learning (RL) problems in which multiple constraint specifications are not identified before training. It is challenging to identify appropriate constraint specifications due to the undefined trade-off between the reward maximization objective and the constraint satisfaction, which is ubiquitous in constrained decision-making. To tackle this issue, we propose a new constrained RL approach that searches for policy and constraint specifications together. This method features the adaptation of relaxing the constraint according to a relaxation cost introduced in the learning objective. Since this feature mimics how ecological systems adapt to disruptions by altering operation, our approach is termed as resilient constrained RL. Specifically, we provide a set of sufficient conditions that balance the constraint satisfaction and the reward maximization in notion of resilient equilibrium, propose a tractable formulation of resilient constrained policy optimization that takes this equilibrium as an optimal solution, and advocate two resilient constrained policy search algorithms with non-asymptotic convergence guarantees on the optimality gap and constraint satisfaction. Furthermore, we demonstrate the merits and the effectiveness of our approach in computational experiments.

Last-Iterate Convergent Policy Gradient Primal-Dual Methods for Constrained MDPs

We study the problem of computing an optimal policy of an infinite-horizon discounted constrained Markov decision process (constrained MDP). Despite the popularity of Lagrangian-based policy search methods used in practice, the oscillation of policy iterates in these methods has not been fully understood, bringing out issues such as violation of constraints and sensitivity to hyper-parameters. To fill this gap, we employ the Lagrangian method to cast a constrained MDP into a constrained saddle-point problem in which max/min players correspond to primal/dual variables, respectively, and develop two single-time-scale policy-based primal-dual algorithms with non-asymptotic convergence of their policy iterates to an optimal constrained policy. Specifically, we first propose a regularized policy gradient primal-dual (RPG-PD) method that updates the policy using an entropy-regularized policy gradient, and the dual via a quadratic-regularized gradient ascent, simultaneously. We prove that the policy primal-dual iterates of RPG-PD converge to a regularized saddle point with a sublinear rate, while the policy iterates converge sublinearly to an optimal constrained policy. We further instantiate RPG-PD in large state or action spaces by including function approximation in policy parametrization, and establish similar sublinear last-iterate policy convergence. Second, we propose an optimistic policy gradient primal-dual (OPG-PD) method that employs the optimistic gradient method to update primal/dual variables, simultaneously. We prove that the policy primal-dual iterates of OPG-PD converge to a saddle point that contains an optimal constrained policy, with a linear rate. To the best of our knowledge, this work appears to be the first non-asymptotic policy last-iterate convergence result for single-time-scale algorithms in constrained MDPs.

Provably Efficient Generalized Lagrangian Policy Optimization for Safe Multi-Agent Reinforcement Learning

We examine online safe multi-agent reinforcement learning using constrained Markov games in which agents compete by maximizing their expected total rewards under a constraint on expected total utilities. Our focus is confined to an episodic two-player zero-sum constrained Markov game with independent transition functions that are unknown to agents, adversarial reward functions, and stochastic utility functions. For such a Markov game, we employ an approach based on the occupancy measure to formulate it as an online constrained saddle-point problem with an explicit constraint. We extend the Lagrange multiplier method in constrained optimization to handle the constraint by creating a generalized Lagrangian with minimax decision primal variables and a dual variable. Next, we develop an upper confidence reinforcement learning algorithm to solve this Lagrangian problem while balancing exploration and exploitation. Our algorithm updates the minimax decision primal variables via online mirror descent and the dual variable via projected gradient step and we prove that it enjoys sublinear rate $ O((|X|+|Y|) L \sqrt{T(|A|+|B|)}))$ for both regret and constraint violation after playing $T$ episodes of the game. Here, $L$ is the horizon of each episode, $(|X|,|A|)$ and $(|Y|,|B|)$ are the state/action space sizes of the min-player and the max-player, respectively. To the best of our knowledge, we provide the first provably efficient online safe reinforcement learning algorithm in constrained Markov games.

Convergence and sample complexity of natural policy gradient primal-dual methods for constrained MDPs

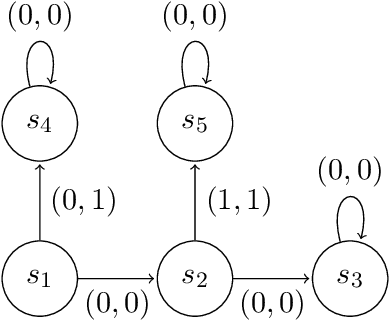
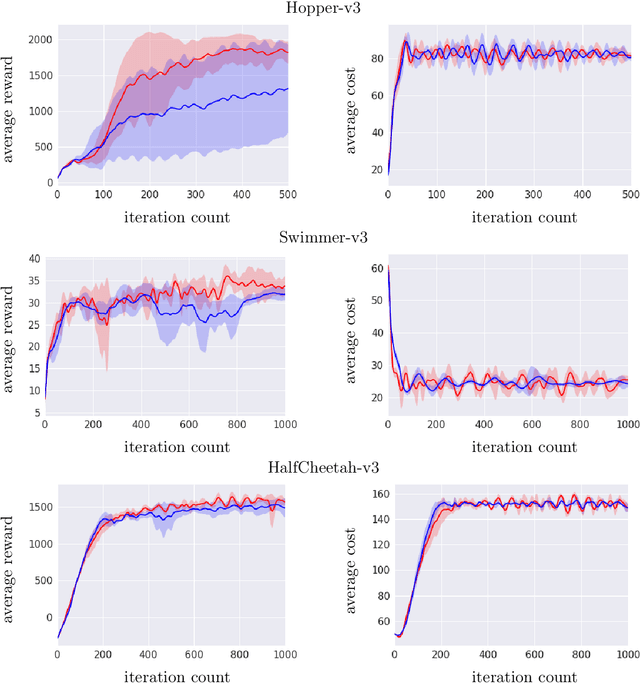
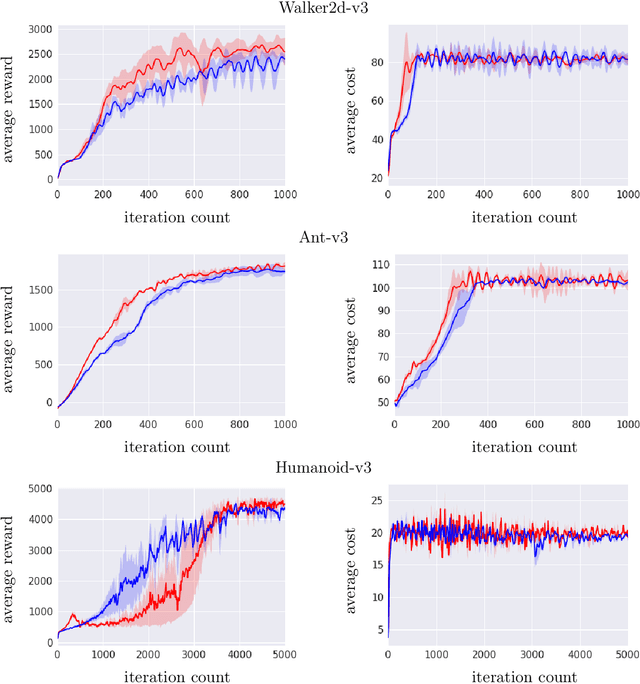
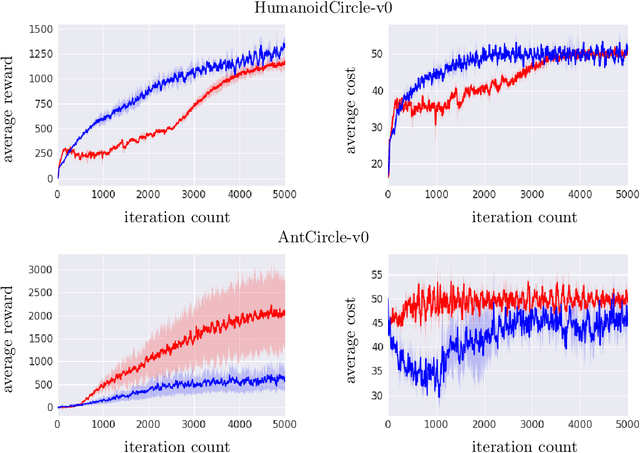
We study sequential decision making problems aimed at maximizing the expected total reward while satisfying a constraint on the expected total utility. We employ the natural policy gradient method to solve the discounted infinite-horizon optimal control problem for Constrained Markov Decision Processes (constrained MDPs). Specifically, we propose a new Natural Policy Gradient Primal-Dual (NPG-PD) method that updates the primal variable via natural policy gradient ascent and the dual variable via projected sub-gradient descent. Although the underlying maximization involves a nonconcave objective function and a nonconvex constraint set, under the softmax policy parametrization we prove that our method achieves global convergence with sublinear rates regarding both the optimality gap and the constraint violation. Such convergence is independent of the size of the state-action space, i.e., it is~dimension-free. Furthermore, for log-linear and general smooth policy parametrizations, we establish sublinear convergence rates up to a function approximation error caused by restricted policy parametrization. We also provide convergence and finite-sample complexity guarantees for two sample-based NPG-PD algorithms. Finally, we use computational experiments to showcase the merits and the effectiveness of our approach.

Independent Policy Gradient for Large-Scale Markov Potential Games: Sharper Rates, Function Approximation, and Game-Agnostic Convergence

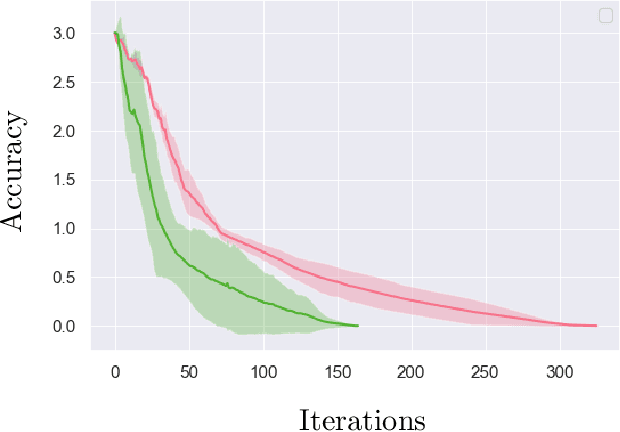
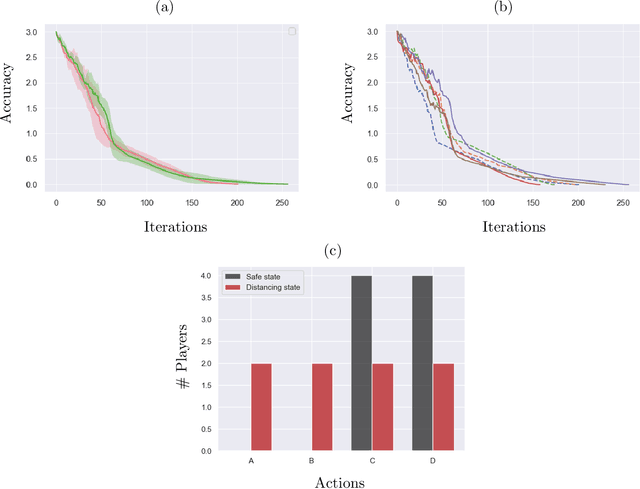
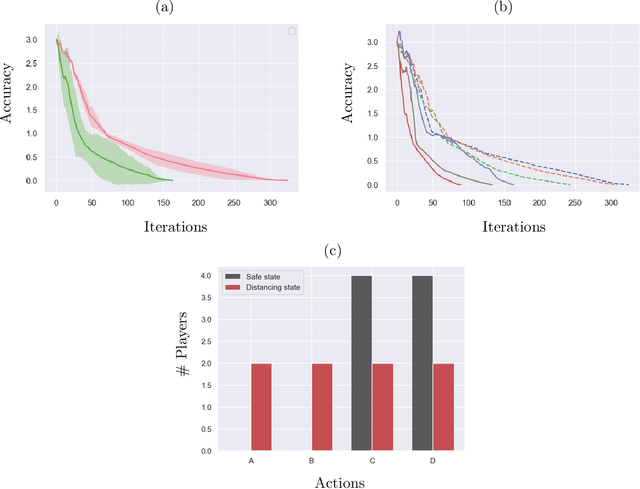
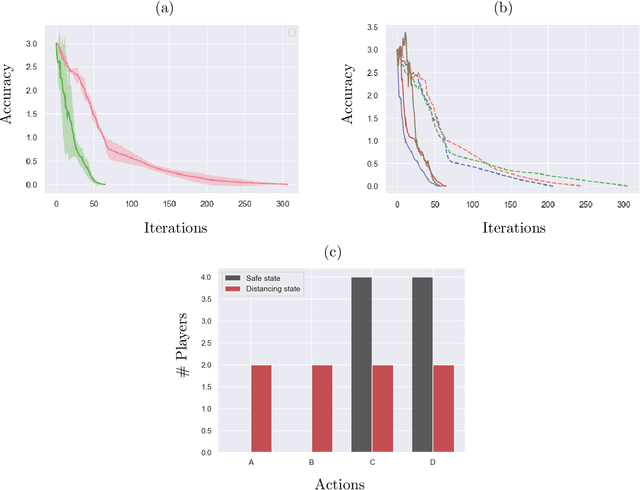
We examine global non-asymptotic convergence properties of policy gradient methods for multi-agent reinforcement learning (RL) problems in Markov potential games (MPG). To learn a Nash equilibrium of an MPG in which the size of state space and/or the number of players can be very large, we propose new independent policy gradient algorithms that are run by all players in tandem. When there is no uncertainty in the gradient evaluation, we show that our algorithm finds an $\epsilon$-Nash equilibrium with $O(1/\epsilon^2)$ iteration complexity which does not explicitly depend on the state space size. When the exact gradient is not available, we establish $O(1/\epsilon^5)$ sample complexity bound in a potentially infinitely large state space for a sample-based algorithm that utilizes function approximation. Moreover, we identify a class of independent policy gradient algorithms that enjoys convergence for both zero-sum Markov games and Markov cooperative games with the players that are oblivious to the types of games being played. Finally, we provide computational experiments to corroborate the merits and the effectiveness of our theoretical developments.