LoRTA: Low Rank Tensor Adaptation of Large Language Models

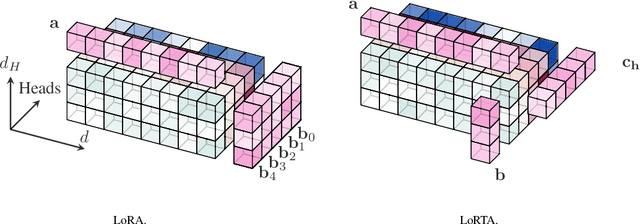
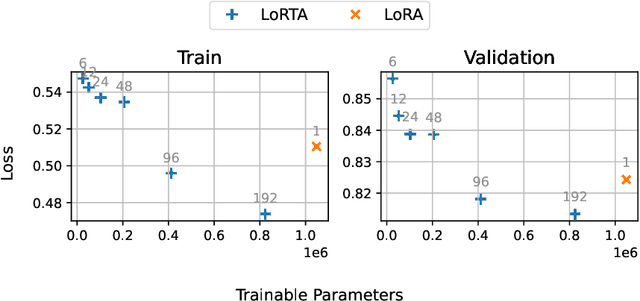
Low Rank Adaptation (LoRA) is a popular Parameter Efficient Fine Tuning (PEFT) method that effectively adapts large pre-trained models for downstream tasks. LoRA parameterizes model updates using low-rank matrices at each layer, significantly reducing the number of trainable parameters and, consequently, resource requirements during fine-tuning. However, the lower bound on the number of trainable parameters remains high due to the use of the low-rank matrix model. In this paper, we address this limitation by proposing a novel approach that employs a low rank tensor parametrization for model updates. The proposed low rank tensor model can significantly reduce the number of trainable parameters, while also allowing for finer-grained control over adapter size. Our experiments on Natural Language Understanding, Instruction Tuning, Preference Optimization and Protein Folding benchmarks demonstrate that our method is both efficient and effective for fine-tuning large language models, achieving a substantial reduction in the number of parameters while maintaining comparable performance.

Loss Shaping Constraints for Long-Term Time Series Forecasting

Several applications in time series forecasting require predicting multiple steps ahead. Despite the vast amount of literature in the topic, both classical and recent deep learning based approaches have mostly focused on minimising performance averaged over the predicted window. We observe that this can lead to disparate distributions of errors across forecasting steps, especially for recent transformer architectures trained on popular forecasting benchmarks. That is, optimising performance on average can lead to undesirably large errors at specific time-steps. In this work, we present a Constrained Learning approach for long-term time series forecasting that aims to find the best model in terms of average performance that respects a user-defined upper bound on the loss at each time-step. We call our approach loss shaping constraints because it imposes constraints on the loss at each time step, and leverage recent duality results to show that despite its non-convexity, the resulting problem has a bounded duality gap. We propose a practical Primal-Dual algorithm to tackle it, and demonstrate that the proposed approach exhibits competitive average performance in time series forecasting benchmarks, while shaping the distribution of errors across the predicted window.

Resilient Constrained Learning

When deploying machine learning solutions, they must satisfy multiple requirements beyond accuracy, such as fairness, robustness, or safety. These requirements are imposed during training either implicitly, using penalties, or explicitly, using constrained optimization methods based on Lagrangian duality. Either way, specifying requirements is hindered by the presence of compromises and limited prior knowledge about the data. Furthermore, their impact on performance can often only be evaluated by actually solving the learning problem. This paper presents a constrained learning approach that adapts the requirements while simultaneously solving the learning task. To do so, it relaxes the learning constraints in a way that contemplates how much they affect the task at hand by balancing the performance gains obtained from the relaxation against a user-defined cost of that relaxation. We call this approach resilient constrained learning after the term used to describe ecological systems that adapt to disruptions by modifying their operation. We show conditions under which this balance can be achieved and introduce a practical algorithm to compute it, for which we derive approximation and generalization guarantees. We showcase the advantages of this resilient learning method in image classification tasks involving multiple potential invariances and in heterogeneous federated learning.

Neural Networks with Quantization Constraints

Enabling low precision implementations of deep learning models, without considerable performance degradation, is necessary in resource and latency constrained settings. Moreover, exploiting the differences in sensitivity to quantization across layers can allow mixed precision implementations to achieve a considerably better computation performance trade-off. However, backpropagating through the quantization operation requires introducing gradient approximations, and choosing which layers to quantize is challenging for modern architectures due to the large search space. In this work, we present a constrained learning approach to quantization aware training. We formulate low precision supervised learning as a constrained optimization problem, and show that despite its non-convexity, the resulting problem is strongly dual and does away with gradient estimations. Furthermore, we show that dual variables indicate the sensitivity of the objective with respect to constraint perturbations. We demonstrate that the proposed approach exhibits competitive performance in image classification tasks, and leverage the sensitivity result to apply layer selective quantization based on the value of dual variables, leading to considerable performance improvements.

Automatic Data Augmentation via Invariance-Constrained Learning

Underlying data structures, such as symmetries or invariances to transformations, are often exploited to improve the solution of learning tasks. However, embedding these properties in models or learning algorithms can be challenging and computationally intensive. Data augmentation, on the other hand, induces these symmetries during training by applying multiple transformations to the input data. Despite its ubiquity, its effectiveness depends on the choices of which transformations to apply, when to do so, and how often. In fact, there is both empirical and theoretical evidence that the indiscriminate use of data augmentation can introduce biases that outweigh its benefits. This work tackles these issues by automatically adapting the data augmentation while solving the learning task. To do so, it formulates data augmentation as an invariance-constrained learning problem and leverages Monte Carlo Markov Chain (MCMC) sampling to solve it. The result is a practical algorithm that not only does away with a priori searches for augmentation distributions, but also dynamically controls if and when data augmentation is applied. Our experiments illustrate the performance of this method, which achieves state-of-the-art results in automatic data augmentation benchmarks for CIFAR datasets. Furthermore, this approach can be used to gather insights on the actual symmetries underlying a learning task.