Cooper: A Library for Constrained Optimization in Deep Learning

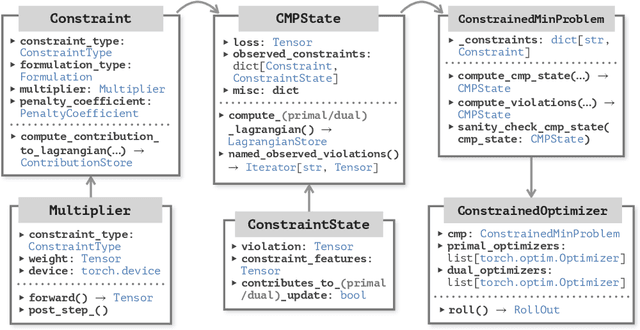
Cooper is an open-source package for solving constrained optimization problems involving deep learning models. Cooper implements several Lagrangian-based first-order update schemes, making it easy to combine constrained optimization algorithms with high-level features of PyTorch such as automatic differentiation, and specialized deep learning architectures and optimizers. Although Cooper is specifically designed for deep learning applications where gradients are estimated based on mini-batches, it is suitable for general non-convex continuous constrained optimization. Cooper's source code is available at https://github.com/cooper-org/cooper.

Feasible Learning

We introduce Feasible Learning (FL), a sample-centric learning paradigm where models are trained by solving a feasibility problem that bounds the loss for each training sample. In contrast to the ubiquitous Empirical Risk Minimization (ERM) framework, which optimizes for average performance, FL demands satisfactory performance on every individual data point. Since any model that meets the prescribed performance threshold is a valid FL solution, the choice of optimization algorithm and its dynamics play a crucial role in shaping the properties of the resulting solutions. In particular, we study a primal-dual approach which dynamically re-weights the importance of each sample during training. To address the challenge of setting a meaningful threshold in practice, we introduce a relaxation of FL that incorporates slack variables of minimal norm. Our empirical analysis, spanning image classification, age regression, and preference optimization in large language models, demonstrates that models trained via FL can learn from data while displaying improved tail behavior compared to ERM, with only a marginal impact on average performance.

On PI Controllers for Updating Lagrange Multipliers in Constrained Optimization

Constrained optimization offers a powerful framework to prescribe desired behaviors in neural network models. Typically, constrained problems are solved via their min-max Lagrangian formulations, which exhibit unstable oscillatory dynamics when optimized using gradient descent-ascent. The adoption of constrained optimization techniques in the machine learning community is currently limited by the lack of reliable, general-purpose update schemes for the Lagrange multipliers. This paper proposes the $\nu$PI algorithm and contributes an optimization perspective on Lagrange multiplier updates based on PI controllers, extending the work of Stooke, Achiam and Abbeel (2020). We provide theoretical and empirical insights explaining the inability of momentum methods to address the shortcomings of gradient descent-ascent, and contrast this with the empirical success of our proposed $\nu$PI controller. Moreover, we prove that $\nu$PI generalizes popular momentum methods for single-objective minimization. Our experiments demonstrate that $\nu$PI reliably stabilizes the multiplier dynamics and its hyperparameters enjoy robust and predictable behavior.

Balancing Act: Constraining Disparate Impact in Sparse Models

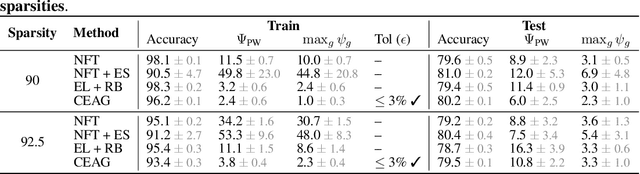
Model pruning is a popular approach to enable the deployment of large deep learning models on edge devices with restricted computational or storage capacities. Although sparse models achieve performance comparable to that of their dense counterparts at the level of the entire dataset, they exhibit high accuracy drops for some data sub-groups. Existing methods to mitigate this disparate impact induced by pruning (i) rely on surrogate metrics that address the problem indirectly and have limited interpretability; or (ii) scale poorly with the number of protected sub-groups in terms of computational cost. We propose a constrained optimization approach that $\textit{directly addresses the disparate impact of pruning}$: our formulation bounds the accuracy change between the dense and sparse models, for each sub-group. This choice of constraints provides an interpretable success criterion to determine if a pruned model achieves acceptable disparity levels. Experimental results demonstrate that our technique scales reliably to problems involving large models and hundreds of protected sub-groups.

Omega: Optimistic EMA Gradients

Stochastic min-max optimization has gained interest in the machine learning community with the advancements in GANs and adversarial training. Although game optimization is fairly well understood in the deterministic setting, some issues persist in the stochastic regime. Recent work has shown that stochastic gradient descent-ascent methods such as the optimistic gradient are highly sensitive to noise or can fail to converge. Although alternative strategies exist, they can be prohibitively expensive. We introduce Omega, a method with optimistic-like updates that mitigates the impact of noise by incorporating an EMA of historic gradients in its update rule. We also explore a variation of this algorithm that incorporates momentum. Although we do not provide convergence guarantees, our experiments on stochastic games show that Omega outperforms the optimistic gradient method when applied to linear players.

Controlled Sparsity via Constrained Optimization or: How I Learned to Stop Tuning Penalties and Love Constraints

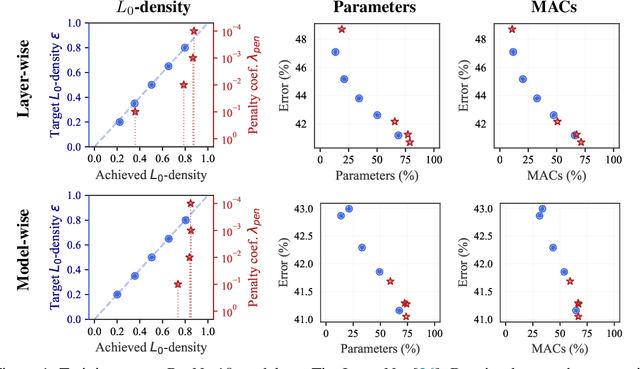
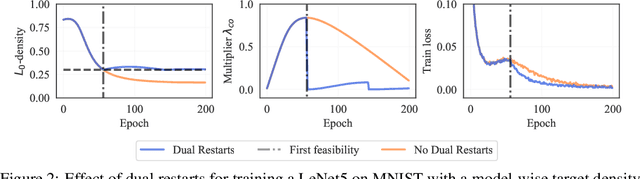
The performance of trained neural networks is robust to harsh levels of pruning. Coupled with the ever-growing size of deep learning models, this observation has motivated extensive research on learning sparse models. In this work, we focus on the task of controlling the level of sparsity when performing sparse learning. Existing methods based on sparsity-inducing penalties involve expensive trial-and-error tuning of the penalty factor, thus lacking direct control of the resulting model sparsity. In response, we adopt a constrained formulation: using the gate mechanism proposed by Louizos et al. (2018), we formulate a constrained optimization problem where sparsification is guided by the training objective and the desired sparsity target in an end-to-end fashion. Experiments on CIFAR-10/100, TinyImageNet, and ImageNet using WideResNet and ResNet{18, 50} models validate the effectiveness of our proposal and demonstrate that we can reliably achieve pre-determined sparsity targets without compromising on predictive performance.

L$_0$onie: Compressing COINs with L$_0$-constraints

Advances in Implicit Neural Representations (INR) have motivated research on domain-agnostic compression techniques. These methods train a neural network to approximate an object, and then store the weights of the trained model. For example, given an image, a network is trained to learn the mapping from pixel locations to RGB values. In this paper, we propose L$_0$onie, a sparsity-constrained extension of the COIN compression method. Sparsity allows to leverage the faster learning of overparameterized networks, while retaining the desirable compression rate of smaller models. Moreover, our constrained formulation ensures that the final model respects a pre-determined compression rate, dispensing of the need for expensive architecture search.

Covariance Estimation from Compressive Data Partitions using a Projected Gradient-based Algorithm

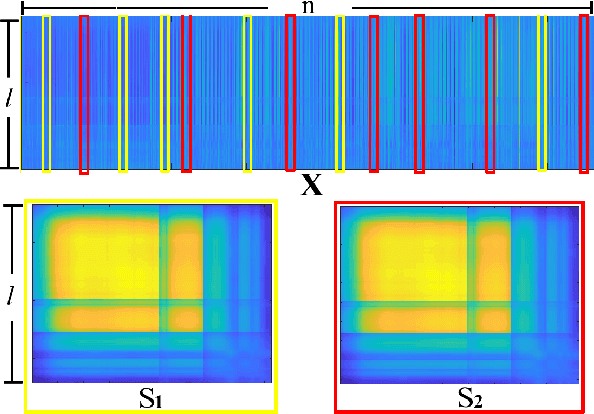
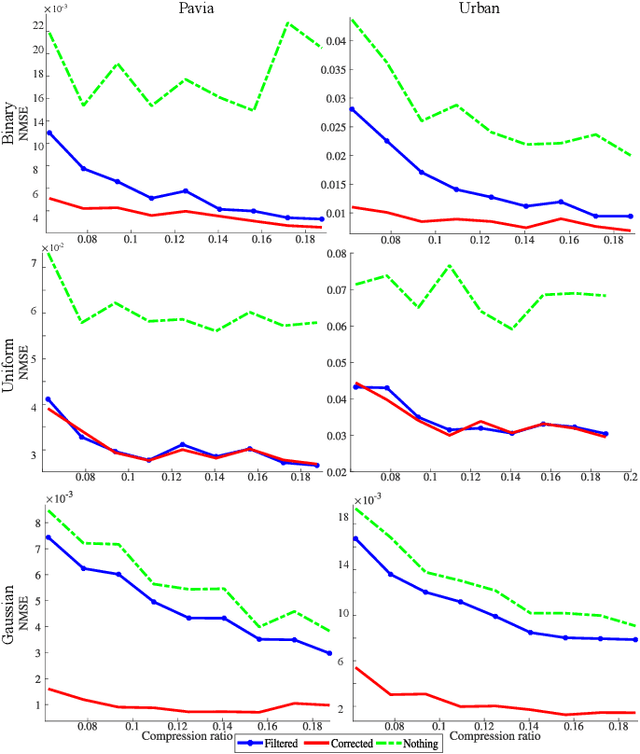
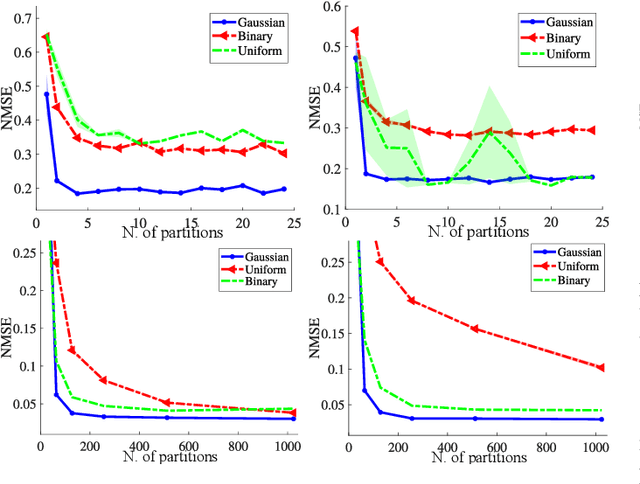
Covariance matrix estimation techniques require high acquisition costs that challenge the sampling systems' storing and transmission capabilities. For this reason, various acquisition approaches have been developed to simultaneously sense and compress the relevant information of the signal using random projections. However, estimating the covariance matrix from the random projections is an ill-posed problem that requires further information about the data, such as sparsity, low rank, or stationary behavior. Furthermore, this approach fails using high compression ratios. Therefore, this paper proposes an algorithm based on the projected gradient method to recover a low-rank or Toeplitz approximation of the covariance matrix. The proposed algorithm divides the data into subsets projected onto different subspaces, assuming that each subset contains an approximation of the signal statistics, improving the inverse problem's condition. The error induced by this assumption is analytically derived along with the convergence guarantees of the proposed method. Extensive simulations show that the proposed algorithm can effectively recover the covariance matrix of hyperspectral images with high compression ratios (8-15% approx) in noisy scenarios. Additionally, simulations and theoretical results show that filtering the gradient reduces the estimator's error recovering up to twice the number of eigenvectors.