ICL-TSVD: Bridging Theory and Practice in Continual Learning with Pre-trained Models

The goal of continual learning (CL) is to train a model that can solve multiple tasks presented sequentially. Recent CL approaches have achieved strong performance by leveraging large pre-trained models that generalize well to downstream tasks. However, such methods lack theoretical guarantees, making them prone to unexpected failures. Conversely, principled CL approaches often fail to achieve competitive performance. In this work, we bridge this gap between theory and practice by integrating an empirically strong approach (RanPAC) into a principled framework, Ideal Continual Learner (ICL), designed to prevent forgetting. Specifically, we lift pre-trained features into a higher dimensional space and formulate an over-parametrized minimum-norm least-squares problem. We find that the lifted features are highly ill-conditioned, potentially leading to large training errors (numerical instability) and increased generalization errors (double descent). We address these challenges by continually truncating the singular value decomposition (SVD) of the lifted features. Our approach, termed ICL-TSVD, is stable with respect to the choice of hyperparameters, can handle hundreds of tasks, and outperforms state-of-the-art CL methods on multiple datasets. Importantly, our method satisfies a recurrence relation throughout its continual learning process, which allows us to prove it maintains small training and generalization errors by appropriately truncating a fraction of SVD factors. This results in a stable continual learning method with strong empirical performance and theoretical guarantees.

Near-Optimal Solutions of Constrained Learning Problems

With the widespread adoption of machine learning systems, the need to curtail their behavior has become increasingly apparent. This is evidenced by recent advancements towards developing models that satisfy robustness, safety, and fairness requirements. These requirements can be imposed (with generalization guarantees) by formulating constrained learning problems that can then be tackled by dual ascent algorithms. Yet, though these algorithms converge in objective value, even in non-convex settings, they cannot guarantee that their outcome is feasible. Doing so requires randomizing over all iterates, which is impractical in virtually any modern applications. Still, final iterates have been observed to perform well in practice. In this work, we address this gap between theory and practice by characterizing the constraint violation of Lagrangian minimizers associated with optimal dual variables, despite lack of convexity. To do this, we leverage the fact that non-convex, finite-dimensional constrained learning problems can be seen as parametrizations of convex, functional problems. Our results show that rich parametrizations effectively mitigate the issue of feasibility in dual methods, shedding light on prior empirical successes of dual learning. We illustrate our findings in fair learning tasks.

Primal-Dual Continual Learning: Stability and Plasticity through Lagrange Multipliers

Continual learning is inherently a constrained learning problem. The goal is to learn a predictor under a \emph{no-forgetting} requirement. Although several prior studies formulate it as such, they do not solve the constrained problem explicitly. In this work, we show that it is both possible and beneficial to undertake the constrained optimization problem directly. To do this, we leverage recent results in constrained learning through Lagrangian duality. We focus on memory-based methods, where a small subset of samples from previous tasks can be stored in a replay buffer. In this setting, we analyze two versions of the continual learning problem: a coarse approach with constraints at the task level and a fine approach with constraints at the sample level. We show that dual variables indicate the sensitivity of the optimal value with respect to constraint perturbations. We then leverage this result to partition the buffer in the coarse approach, allocating more resources to harder tasks, and to populate the buffer in the fine approach, including only impactful samples. We derive sub-optimality bounds, and empirically corroborate our theoretical results in various continual learning benchmarks. We also discuss the limitations of these methods with respect to the amount of memory available and the number of constraints involved in the optimization problem.

Neural Networks with Quantization Constraints

Enabling low precision implementations of deep learning models, without considerable performance degradation, is necessary in resource and latency constrained settings. Moreover, exploiting the differences in sensitivity to quantization across layers can allow mixed precision implementations to achieve a considerably better computation performance trade-off. However, backpropagating through the quantization operation requires introducing gradient approximations, and choosing which layers to quantize is challenging for modern architectures due to the large search space. In this work, we present a constrained learning approach to quantization aware training. We formulate low precision supervised learning as a constrained optimization problem, and show that despite its non-convexity, the resulting problem is strongly dual and does away with gradient estimations. Furthermore, we show that dual variables indicate the sensitivity of the objective with respect to constraint perturbations. We demonstrate that the proposed approach exhibits competitive performance in image classification tasks, and leverage the sensitivity result to apply layer selective quantization based on the value of dual variables, leading to considerable performance improvements.

A Lagrangian Duality Approach to Active Learning

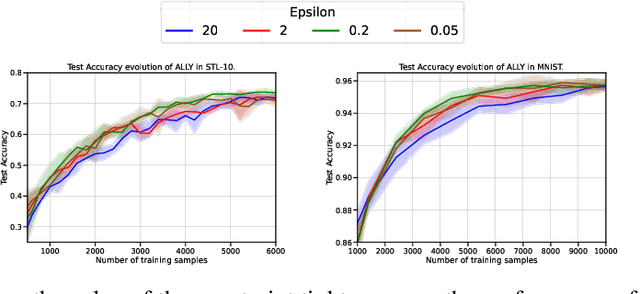
We consider the batch active learning problem, where only a subset of the training data is labeled, and the goal is to query a batch of unlabeled samples to be labeled so as to maximally improve model performance. We formulate the learning problem using constrained optimization, where each constraint bounds the performance of the model on labeled samples. Considering a primal-dual approach, we optimize the primal variables, corresponding to the model parameters, as well as the dual variables, corresponding to the constraints. As each dual variable indicates how significantly the perturbation of the respective constraint affects the optimal value of the objective function, we use it as a proxy of the informativeness of the corresponding training sample. Our approach, which we refer to as Active Learning via Lagrangian dualitY, or ALLY, leverages this fact to select a diverse set of unlabeled samples with the highest estimated dual variables as our query set. We show, via numerical experiments, that our proposed approach performs similarly to or better than state-of-the-art active learning methods in a variety of classification and regression tasks. We also demonstrate how ALLY can be used in a generative mode to create novel, maximally-informative samples. The implementation code for ALLY can be found at https://github.com/juanelenter/ALLY.