Cooper: A Library for Constrained Optimization in Deep Learning

Cooper is an open-source package for solving constrained optimization problems involving deep learning models. Cooper implements several Lagrangian-based first-order update schemes, making it easy to combine constrained optimization algorithms with high-level features of PyTorch such as automatic differentiation, and specialized deep learning architectures and optimizers. Although Cooper is specifically designed for deep learning applications where gradients are estimated based on mini-batches, it is suitable for general non-convex continuous constrained optimization. Cooper's source code is available at https://github.com/cooper-org/cooper.

Feasible Learning

We introduce Feasible Learning (FL), a sample-centric learning paradigm where models are trained by solving a feasibility problem that bounds the loss for each training sample. In contrast to the ubiquitous Empirical Risk Minimization (ERM) framework, which optimizes for average performance, FL demands satisfactory performance on every individual data point. Since any model that meets the prescribed performance threshold is a valid FL solution, the choice of optimization algorithm and its dynamics play a crucial role in shaping the properties of the resulting solutions. In particular, we study a primal-dual approach which dynamically re-weights the importance of each sample during training. To address the challenge of setting a meaningful threshold in practice, we introduce a relaxation of FL that incorporates slack variables of minimal norm. Our empirical analysis, spanning image classification, age regression, and preference optimization in large language models, demonstrates that models trained via FL can learn from data while displaying improved tail behavior compared to ERM, with only a marginal impact on average performance.

On PI Controllers for Updating Lagrange Multipliers in Constrained Optimization

Constrained optimization offers a powerful framework to prescribe desired behaviors in neural network models. Typically, constrained problems are solved via their min-max Lagrangian formulations, which exhibit unstable oscillatory dynamics when optimized using gradient descent-ascent. The adoption of constrained optimization techniques in the machine learning community is currently limited by the lack of reliable, general-purpose update schemes for the Lagrange multipliers. This paper proposes the $\nu$PI algorithm and contributes an optimization perspective on Lagrange multiplier updates based on PI controllers, extending the work of Stooke, Achiam and Abbeel (2020). We provide theoretical and empirical insights explaining the inability of momentum methods to address the shortcomings of gradient descent-ascent, and contrast this with the empirical success of our proposed $\nu$PI controller. Moreover, we prove that $\nu$PI generalizes popular momentum methods for single-objective minimization. Our experiments demonstrate that $\nu$PI reliably stabilizes the multiplier dynamics and its hyperparameters enjoy robust and predictable behavior.

Balancing Act: Constraining Disparate Impact in Sparse Models

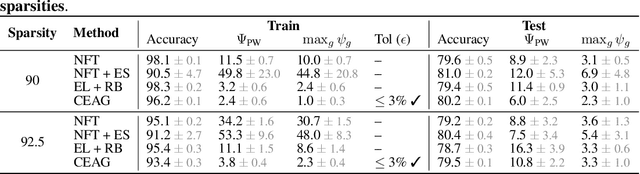
Model pruning is a popular approach to enable the deployment of large deep learning models on edge devices with restricted computational or storage capacities. Although sparse models achieve performance comparable to that of their dense counterparts at the level of the entire dataset, they exhibit high accuracy drops for some data sub-groups. Existing methods to mitigate this disparate impact induced by pruning (i) rely on surrogate metrics that address the problem indirectly and have limited interpretability; or (ii) scale poorly with the number of protected sub-groups in terms of computational cost. We propose a constrained optimization approach that $\textit{directly addresses the disparate impact of pruning}$: our formulation bounds the accuracy change between the dense and sparse models, for each sub-group. This choice of constraints provides an interpretable success criterion to determine if a pruned model achieves acceptable disparity levels. Experimental results demonstrate that our technique scales reliably to problems involving large models and hundreds of protected sub-groups.

A Distributed Data-Parallel PyTorch Implementation of the Distributed Shampoo Optimizer for Training Neural Networks At-Scale

Shampoo is an online and stochastic optimization algorithm belonging to the AdaGrad family of methods for training neural networks. It constructs a block-diagonal preconditioner where each block consists of a coarse Kronecker product approximation to full-matrix AdaGrad for each parameter of the neural network. In this work, we provide a complete description of the algorithm as well as the performance optimizations that our implementation leverages to train deep networks at-scale in PyTorch. Our implementation enables fast multi-GPU distributed data-parallel training by distributing the memory and computation associated with blocks of each parameter via PyTorch's DTensor data structure and performing an AllGather primitive on the computed search directions at each iteration. This major performance enhancement enables us to achieve at most a 10% performance reduction in per-step wall-clock time compared against standard diagonal-scaling-based adaptive gradient methods. We validate our implementation by performing an ablation study on training ImageNet ResNet50, demonstrating Shampoo's superiority over standard training recipes with minimal hyperparameter tuning.

Controlled Sparsity via Constrained Optimization or: How I Learned to Stop Tuning Penalties and Love Constraints

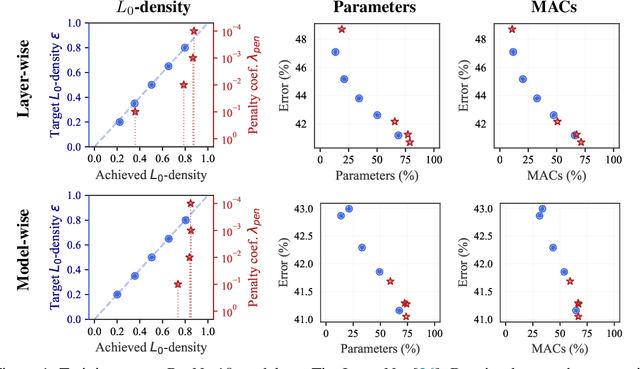
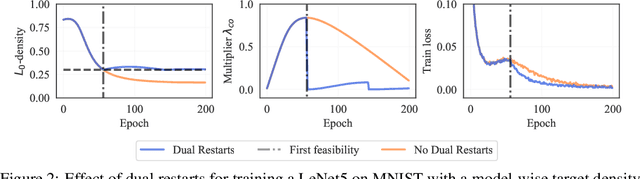
The performance of trained neural networks is robust to harsh levels of pruning. Coupled with the ever-growing size of deep learning models, this observation has motivated extensive research on learning sparse models. In this work, we focus on the task of controlling the level of sparsity when performing sparse learning. Existing methods based on sparsity-inducing penalties involve expensive trial-and-error tuning of the penalty factor, thus lacking direct control of the resulting model sparsity. In response, we adopt a constrained formulation: using the gate mechanism proposed by Louizos et al. (2018), we formulate a constrained optimization problem where sparsification is guided by the training objective and the desired sparsity target in an end-to-end fashion. Experiments on CIFAR-10/100, TinyImageNet, and ImageNet using WideResNet and ResNet{18, 50} models validate the effectiveness of our proposal and demonstrate that we can reliably achieve pre-determined sparsity targets without compromising on predictive performance.

L$_0$onie: Compressing COINs with L$_0$-constraints

Advances in Implicit Neural Representations (INR) have motivated research on domain-agnostic compression techniques. These methods train a neural network to approximate an object, and then store the weights of the trained model. For example, given an image, a network is trained to learn the mapping from pixel locations to RGB values. In this paper, we propose L$_0$onie, a sparsity-constrained extension of the COIN compression method. Sparsity allows to leverage the faster learning of overparameterized networks, while retaining the desirable compression rate of smaller models. Moreover, our constrained formulation ensures that the final model respects a pre-determined compression rate, dispensing of the need for expensive architecture search.

Equivariant Mesh Attention Networks

Equivariance to symmetries has proven to be a powerful inductive bias in deep learning research. Recent works on mesh processing have concentrated on various kinds of natural symmetries, including translations, rotations, scaling, node permutations, and gauge transformations. To date, no existing architecture is equivariant to all of these transformations. Moreover, previous implementations have not always applied these symmetry transformations to the test dataset. This inhibits the ability to determine whether the model attains the claimed equivariance properties. In this paper, we present an attention-based architecture for mesh data that is provably equivariant to all transformations mentioned above. We carry out experiments on the FAUST and TOSCA datasets, and apply the mentioned symmetries to the test set only. Our results confirm that our proposed architecture is equivariant, and therefore robust, to these local/global transformations.

GANGs: Generative Adversarial Network Games

Generative Adversarial Networks (GAN) have become one of the most successful frameworks for unsupervised generative modeling. As GANs are difficult to train much research has focused on this. However, very little of this research has directly exploited game-theoretic techniques. We introduce Generative Adversarial Network Games (GANGs), which explicitly model a finite zero-sum game between a generator ($G$) and classifier ($C$) that use mixed strategies. The size of these games precludes exact solution methods, therefore we define resource-bounded best responses (RBBRs), and a resource-bounded Nash Equilibrium (RB-NE) as a pair of mixed strategies such that neither $G$ or $C$ can find a better RBBR. The RB-NE solution concept is richer than the notion of `local Nash equilibria' in that it captures not only failures of escaping local optima of gradient descent, but applies to any approximate best response computations, including methods with random restarts. To validate our approach, we solve GANGs with the Parallel Nash Memory algorithm, which provably monotonically converges to an RB-NE. We compare our results to standard GAN setups, and demonstrate that our method deals well with typical GAN problems such as mode collapse, partial mode coverage and forgetting.