Edwin D. de Jong
Towards Robust Foundation Models for Digital Pathology
Jul 22, 2025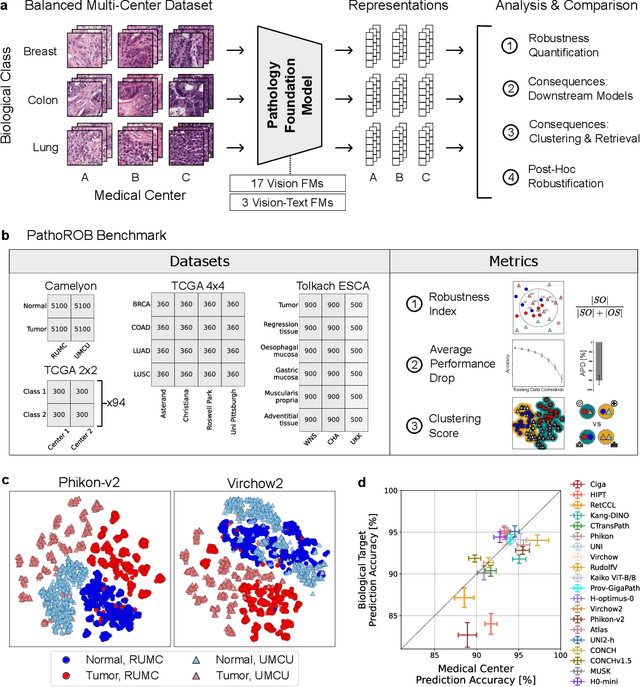
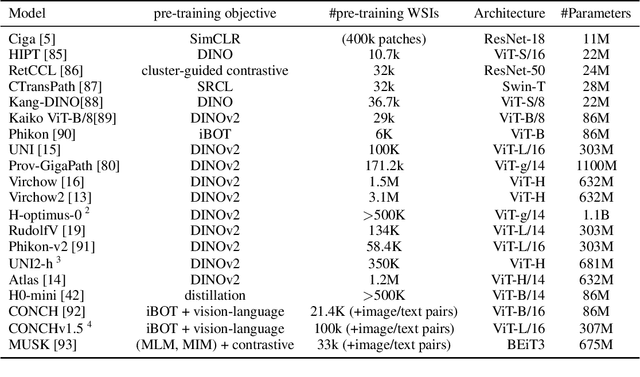
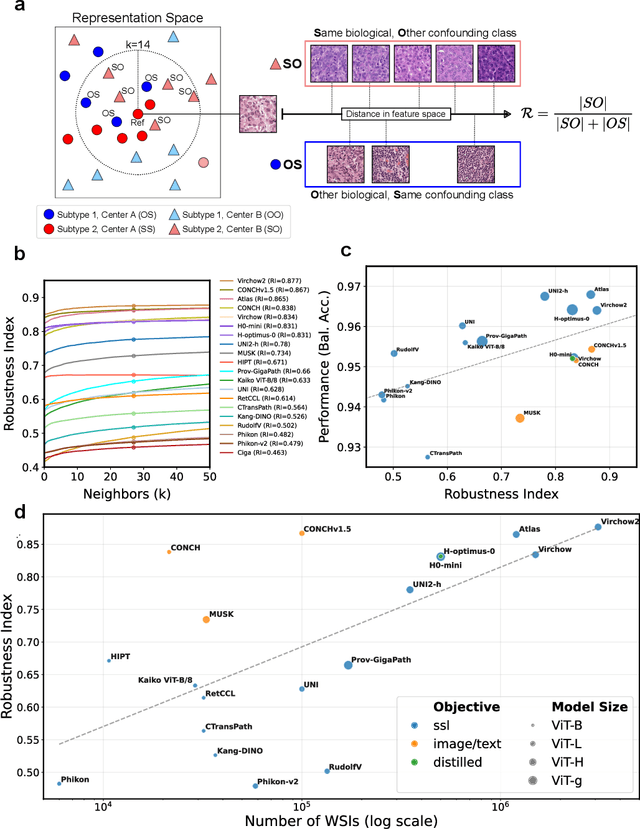

Abstract:Biomedical Foundation Models (FMs) are rapidly transforming AI-enabled healthcare research and entering clinical validation. However, their susceptibility to learning non-biological technical features -- including variations in surgical/endoscopic techniques, laboratory procedures, and scanner hardware -- poses risks for clinical deployment. We present the first systematic investigation of pathology FM robustness to non-biological features. Our work (i) introduces measures to quantify FM robustness, (ii) demonstrates the consequences of limited robustness, and (iii) proposes a framework for FM robustification to mitigate these issues. Specifically, we developed PathoROB, a robustness benchmark with three novel metrics, including the robustness index, and four datasets covering 28 biological classes from 34 medical centers. Our experiments reveal robustness deficits across all 20 evaluated FMs, and substantial robustness differences between them. We found that non-robust FM representations can cause major diagnostic downstream errors and clinical blunders that prevent safe clinical adoption. Using more robust FMs and post-hoc robustification considerably reduced (but did not yet eliminate) the risk of such errors. This work establishes that robustness evaluation is essential for validating pathology FMs before clinical adoption and demonstrates that future FM development must integrate robustness as a core design principle. PathoROB provides a blueprint for assessing robustness across biomedical domains, guiding FM improvement efforts towards more robust, representative, and clinically deployable AI systems that prioritize biological information over technical artifacts.
Foundation Models in Medical Imaging -- A Review and Outlook
Jun 10, 2025Abstract:Foundation models (FMs) are changing the way medical images are analyzed by learning from large collections of unlabeled data. Instead of relying on manually annotated examples, FMs are pre-trained to learn general-purpose visual features that can later be adapted to specific clinical tasks with little additional supervision. In this review, we examine how FMs are being developed and applied in pathology, radiology, and ophthalmology, drawing on evidence from over 150 studies. We explain the core components of FM pipelines, including model architectures, self-supervised learning methods, and strategies for downstream adaptation. We also review how FMs are being used in each imaging domain and compare design choices across applications. Finally, we discuss key challenges and open questions to guide future research.
Current Pathology Foundation Models are unrobust to Medical Center Differences
Jan 29, 2025
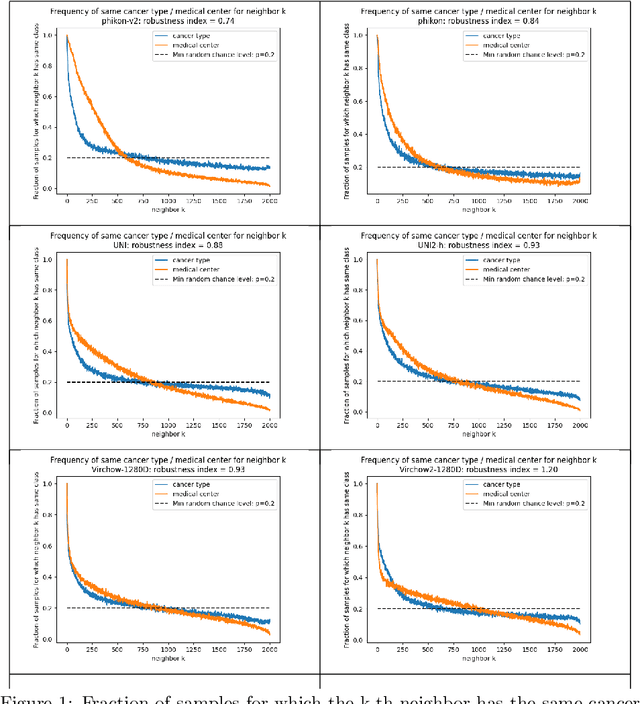
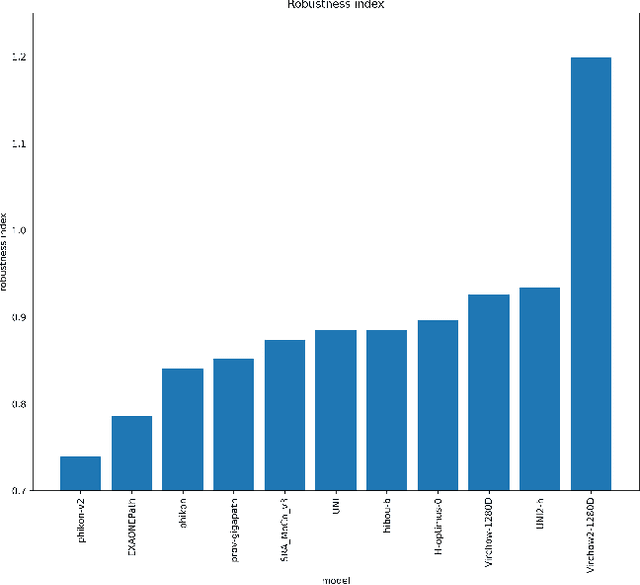
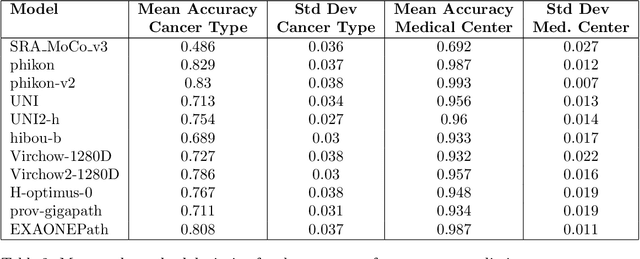
Abstract:Pathology Foundation Models (FMs) hold great promise for healthcare. Before they can be used in clinical practice, it is essential to ensure they are robust to variations between medical centers. We measure whether pathology FMs focus on biological features like tissue and cancer type, or on the well known confounding medical center signatures introduced by staining procedure and other differences. We introduce the Robustness Index. This novel robustness metric reflects to what degree biological features dominate confounding features. Ten current publicly available pathology FMs are evaluated. We find that all current pathology foundation models evaluated represent the medical center to a strong degree. Significant differences in the robustness index are observed. Only one model so far has a robustness index greater than one, meaning biological features dominate confounding features, but only slightly. A quantitative approach to measure the influence of medical center differences on FM-based prediction performance is described. We analyze the impact of unrobustness on classification performance of downstream models, and find that cancer-type classification errors are not random, but specifically attributable to same-center confounders: images of other classes from the same medical center. We visualize FM embedding spaces, and find these are more strongly organized by medical centers than by biological factors. As a consequence, the medical center of origin is predicted more accurately than the tissue source and cancer type. The robustness index introduced here is provided with the aim of advancing progress towards clinical adoption of robust and reliable pathology FMs.
GANGs: Generative Adversarial Network Games
Dec 17, 2017



Abstract:Generative Adversarial Networks (GAN) have become one of the most successful frameworks for unsupervised generative modeling. As GANs are difficult to train much research has focused on this. However, very little of this research has directly exploited game-theoretic techniques. We introduce Generative Adversarial Network Games (GANGs), which explicitly model a finite zero-sum game between a generator ($G$) and classifier ($C$) that use mixed strategies. The size of these games precludes exact solution methods, therefore we define resource-bounded best responses (RBBRs), and a resource-bounded Nash Equilibrium (RB-NE) as a pair of mixed strategies such that neither $G$ or $C$ can find a better RBBR. The RB-NE solution concept is richer than the notion of `local Nash equilibria' in that it captures not only failures of escaping local optima of gradient descent, but applies to any approximate best response computations, including methods with random restarts. To validate our approach, we solve GANGs with the Parallel Nash Memory algorithm, which provably monotonically converges to an RB-NE. We compare our results to standard GAN setups, and demonstrate that our method deals well with typical GAN problems such as mode collapse, partial mode coverage and forgetting.
Incremental Sequence Learning
Dec 01, 2016



Abstract:Deep learning research over the past years has shown that by increasing the scope or difficulty of the learning problem over time, increasingly complex learning problems can be addressed. We study incremental learning in the context of sequence learning, using generative RNNs in the form of multi-layer recurrent Mixture Density Networks. While the potential of incremental or curriculum learning to enhance learning is known, indiscriminate application of the principle does not necessarily lead to improvement, and it is essential therefore to know which forms of incremental or curriculum learning have a positive effect. This research contributes to that aim by comparing three instantiations of incremental or curriculum learning. We introduce Incremental Sequence Learning, a simple incremental approach to sequence learning. Incremental Sequence Learning starts out by using only the first few steps of each sequence as training data. Each time a performance criterion has been reached, the length of the parts of the sequences used for training is increased. We introduce and make available a novel sequence learning task and data set: predicting and classifying MNIST pen stroke sequences. We find that Incremental Sequence Learning greatly speeds up sequence learning and reaches the best test performance level of regular sequence learning 20 times faster, reduces the test error by 74%, and in general performs more robustly; it displays lower variance and achieves sustained progress after all three comparison methods have stopped improving. The other instantiations of curriculum learning do not result in any noticeable improvement. A trained sequence prediction model is also used in transfer learning to the task of sequence classification, where it is found that transfer learning realizes improved classification performance compared to methods that learn to classify from scratch.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge