Rahul Savani
MACS: Multi-Agent Reinforcement Learning for Optimization of Crystal Structures
Jun 04, 2025Abstract:Geometry optimization of atomic structures is a common and crucial task in computational chemistry and materials design. Following the learning to optimize paradigm, we propose a new multi-agent reinforcement learning method called Multi-Agent Crystal Structure optimization (MACS) to address periodic crystal structure optimization. MACS treats geometry optimization as a partially observable Markov game in which atoms are agents that adjust their positions to collectively discover a stable configuration. We train MACS across various compositions of reported crystalline materials to obtain a policy that successfully optimizes structures from the training compositions as well as structures of larger sizes and unseen compositions, confirming its excellent scalability and zero-shot transferability. We benchmark our approach against a broad range of state-of-the-art optimization methods and demonstrate that MACS optimizes periodic crystal structures significantly faster, with fewer energy calculations, and the lowest failure rate.
From Natural Language to Extensive-Form Game Representations
Jan 31, 2025

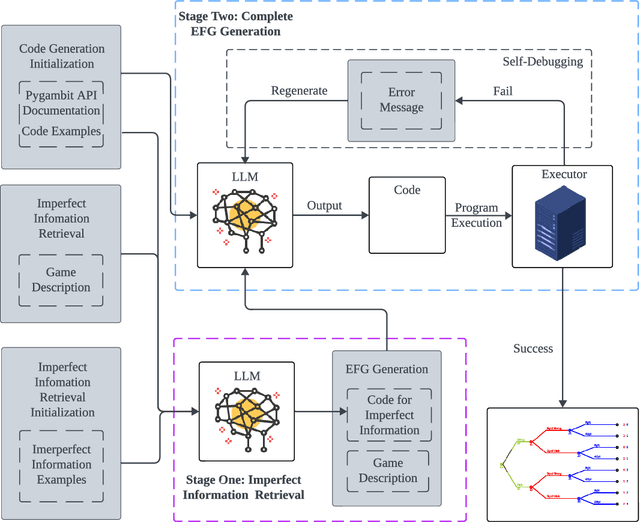
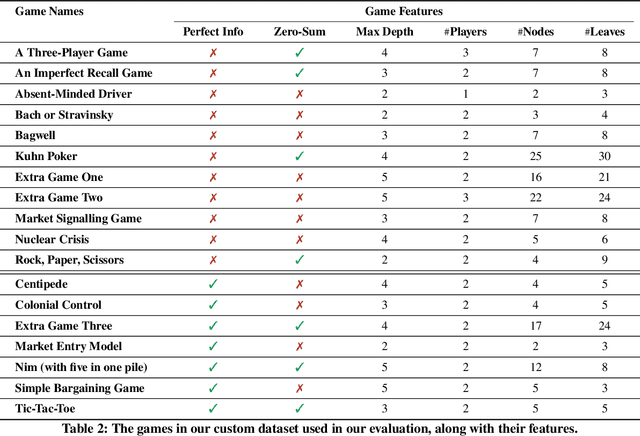
Abstract:We introduce a framework for translating game descriptions in natural language into extensive-form representations in game theory, leveraging Large Language Models (LLMs) and in-context learning. Given the varying levels of strategic complexity in games, such as perfect versus imperfect information, directly applying in-context learning would be insufficient. To address this, we introduce a two-stage framework with specialized modules to enhance in-context learning, enabling it to divide and conquer the problem effectively. In the first stage, we tackle the challenge of imperfect information by developing a module that identifies information sets along and the corresponding partial tree structure. With this information, the second stage leverages in-context learning alongside a self-debugging module to produce a complete extensive-form game tree represented using pygambit, the Python API of a recognized game-theoretic analysis tool called Gambit. Using this python representation enables the automation of tasks such as computing Nash equilibria directly from natural language descriptions. We evaluate the performance of the full framework, as well as its individual components, using various LLMs on games with different levels of strategic complexity. Our experimental results show that the framework significantly outperforms baseline models in generating accurate extensive-form games, with each module playing a critical role in its success.
Assessing data-driven predictions of band gap and electrical conductivity for transparent conducting materials
Nov 21, 2024Abstract:Machine Learning (ML) has offered innovative perspectives for accelerating the discovery of new functional materials, leveraging the increasing availability of material databases. Despite the promising advances, data-driven methods face constraints imposed by the quantity and quality of available data. Moreover, ML is often employed in tandem with simulated datasets originating from density functional theory (DFT), and assessed through in-sample evaluation schemes. This scenario raises questions about the practical utility of ML in uncovering new and significant material classes for industrial applications. Here, we propose a data-driven framework aimed at accelerating the discovery of new transparent conducting materials (TCMs), an important category of semiconductors with a wide range of applications. To mitigate the shortage of available data, we create and validate unique experimental databases, comprising several examples of existing TCMs. We assess state-of-the-art (SOTA) ML models for property prediction from the stoichiometry alone. We propose a bespoke evaluation scheme to provide empirical evidence on the ability of ML to uncover new, previously unseen materials of interest. We test our approach on a list of 55 compositions containing typical elements of known TCMs. Although our study indicates that ML tends to identify new TCMs compositionally similar to those in the training data, we empirically demonstrate that it can highlight material candidates that may have been previously overlooked, offering a systematic approach to identify materials that are likely to display TCMs characteristics.
Policy Space Response Oracles: A Survey
Mar 04, 2024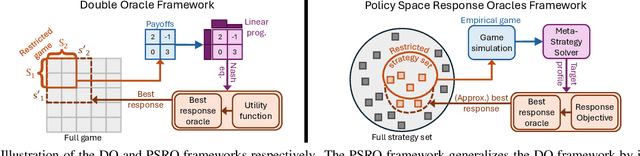

Abstract:In game theory, a game refers to a model of interaction among rational decision-makers or players, making choices with the goal of achieving their individual objectives. Understanding their behavior in games is often referred to as game reasoning. This survey provides a comprehensive overview of a fast-developing game-reasoning framework for large games, known as Policy Space Response Oracles (PSRO). We first motivate PSRO, provide historical context, and position PSRO within game-reasoning approaches. We then focus on the strategy exploration issue for PSRO, the challenge of assembling an effective strategy portfolio for modeling the underlying game with minimum computational cost. We also survey current research directions for enhancing the efficiency of PSRO, and explore the applications of PSRO across various domains. We conclude by discussing open questions and future research.
Conditional Generators for Limit Order Book Environments: Explainability, Challenges, and Robustness
Jun 22, 2023Abstract:Limit order books are a fundamental and widespread market mechanism. This paper investigates the use of conditional generative models for order book simulation. For developing a trading agent, this approach has drawn recent attention as an alternative to traditional backtesting due to its ability to react to the presence of the trading agent. Using a state-of-the-art CGAN (from Coletta et al. (2022)), we explore its dependence upon input features, which highlights both strengths and weaknesses. To do this, we use "adversarial attacks" on the model's features and its mechanism. We then show how these insights can be used to improve the CGAN, both in terms of its realism and robustness. We finish by laying out a roadmap for future work.
Ordinal Potential-based Player Rating
Jun 08, 2023Abstract:A two-player symmetric zero-sum game is transitive if for any pure strategies $x$, $y$, $z$, if $x$ is better than $y$, and $y$ is better than $z$, then $x$ is better than $z$. It was recently observed that the Elo rating fails at preserving transitive relations among strategies and therefore cannot correctly extract the transitive component of a game. Our first contribution is to show that the Elo rating actually does preserve transitivity when computed in the right space. Precisely, using a suitable invertible mapping $\varphi$, we first apply $\varphi$ to the game, then compute Elo ratings, then go back to the original space by applying $\varphi^{-1}$. We provide a characterization of transitive games as a weak variant of ordinal potential games with additively separable potential functions. Leveraging this insight, we introduce the concept of transitivity order, the minimum number of invertible mappings required to transform the payoff of a transitive game into (differences of) its potential function. The transitivity order is a tool to classify transitive games, with Elo games being an example of transitive games of order one. Most real-world games have both transitive and non-transitive (cyclic) components, and we use our analysis of transitivity to extract the transitive (potential) component of an arbitrary game. We link transitivity to the known concept of sign-rank: transitive games have sign-rank two; arbitrary games may have higher sign-rank. Using a neural network-based architecture, we learn a decomposition of an arbitrary game into transitive and cyclic components that prioritises capturing the sign pattern of the game. In particular, a transitive game always has just one component in its decomposition, the potential component. We provide a comprehensive evaluation of our methodology using both toy examples and empirical data from real-world games.
Model-based gym environments for limit order book trading
Sep 16, 2022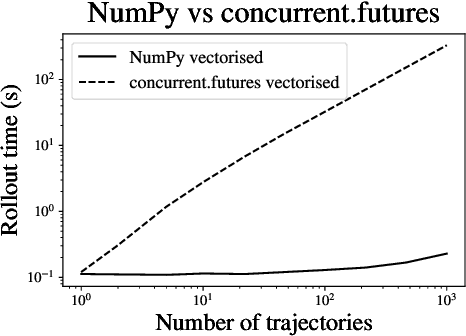


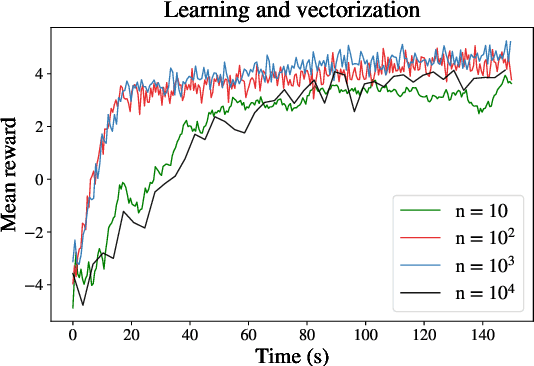
Abstract:Within the mathematical finance literature there is a rich catalogue of mathematical models for studying algorithmic trading problems -- such as market-making and optimal execution -- in limit order books. This paper introduces \mbtgym, a Python module that provides a suite of gym environments for training reinforcement learning (RL) agents to solve such model-based trading problems. The module is set up in an extensible way to allow the combination of different aspects of different models. It supports highly efficient implementations of vectorized environments to allow faster training of RL agents. In this paper, we motivate the challenge of using RL to solve such model-based limit order book problems in mathematical finance, we explain the design of our gym environment, and then demonstrate its use in solving standard and non-standard problems from the literature. Finally, we lay out a roadmap for further development of our module, which we provide as an open source repository on GitHub so that it can serve as a focal point for RL research in model-based algorithmic trading.
Market Making with Scaled Beta Policies
Jul 09, 2022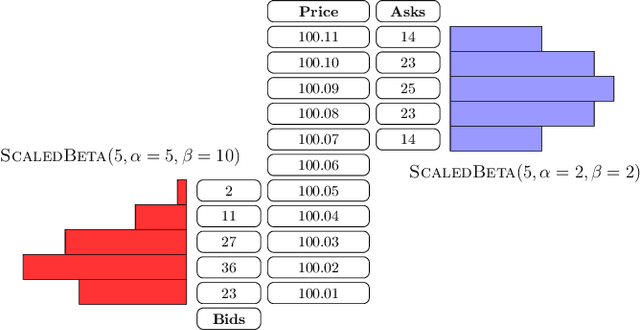
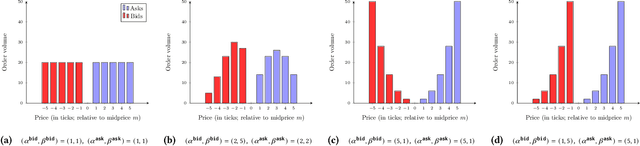
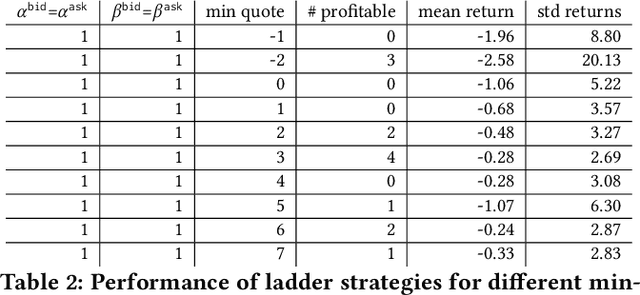
Abstract:This paper introduces a new representation for the actions of a market maker in an order-driven market. This representation uses scaled beta distributions, and generalises three approaches taken in the artificial intelligence for market making literature: single price-level selection, ladder strategies and "market making at the touch". Ladder strategies place uniform volume across an interval of contiguous prices. Scaled beta distribution based policies generalise these, allowing volume to be skewed across the price interval. We demonstrate that this flexibility is useful for inventory management, one of the key challenges faced by a market maker. In this paper, we conduct three main experiments: first, we compare our more flexible beta-based actions with the special case of ladder strategies; then, we investigate the performance of simple fixed distributions; and finally, we devise and evaluate a simple and intuitive dynamic control policy that adjusts actions in a continuous manner depending on the signed inventory that the market maker has acquired. All empirical evaluations use a high-fidelity limit order book simulator based on historical data with 50 levels on each side.
Trading via Selective Classification
Oct 31, 2021
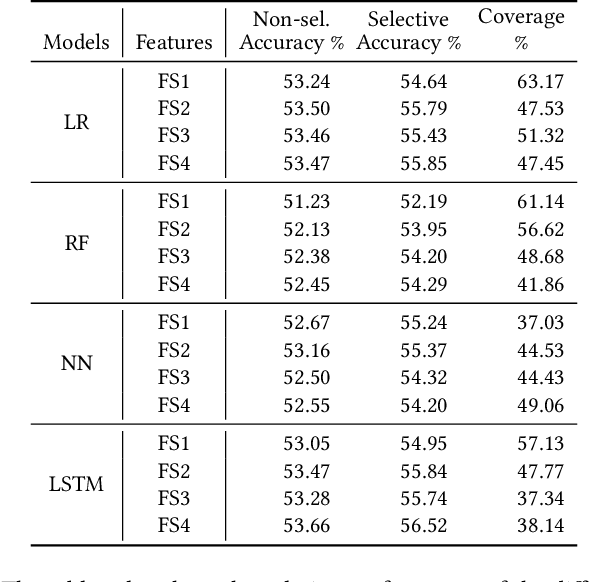
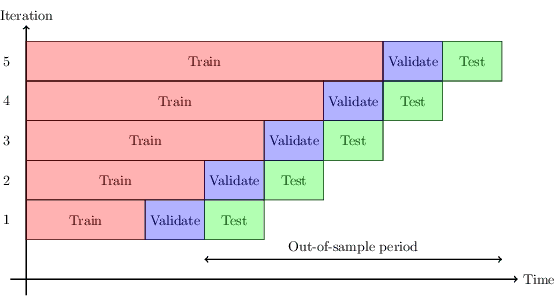
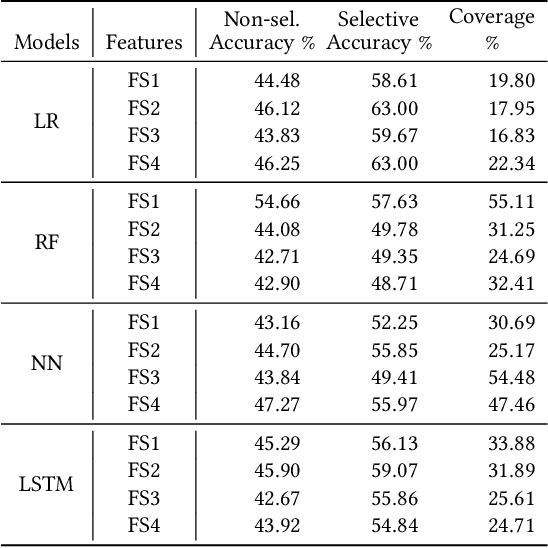
Abstract:A binary classifier that tries to predict if the price of an asset will increase or decrease naturally gives rise to a trading strategy that follows the prediction and thus always has a position in the market. Selective classification extends a binary or many-class classifier to allow it to abstain from making a prediction for certain inputs, thereby allowing a trade-off between the accuracy of the resulting selective classifier against coverage of the input feature space. Selective classifiers give rise to trading strategies that do not take a trading position when the classifier abstains. We investigate the application of binary and ternary selective classification to trading strategy design. For ternary classification, in addition to classes for the price going up or down, we include a third class that corresponds to relatively small price moves in either direction, and gives the classifier another way to avoid making a directional prediction. We use a walk-forward train-validate-test approach to evaluate and compare binary and ternary, selective and non-selective classifiers across several different feature sets based on four classification approaches: logistic regression, random forests, feed-forward, and recurrent neural networks. We then turn these classifiers into trading strategies for which we perform backtests on commodity futures markets. Our empirical results demonstrate the potential of selective classification for trading.
Consensus Multiplicative Weights Update: Learning to Learn using Projector-based Game Signatures
Jun 04, 2021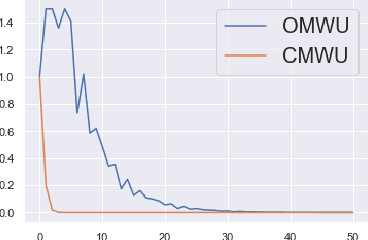

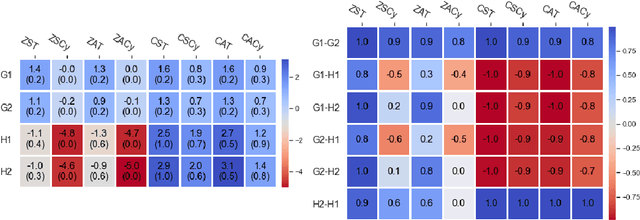
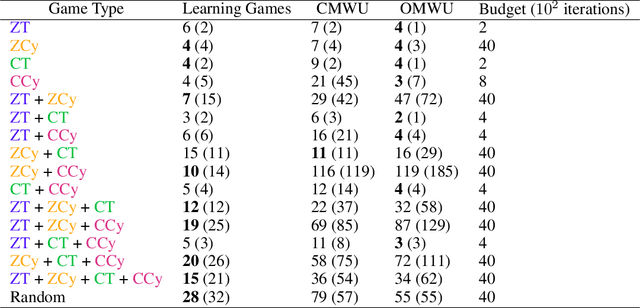
Abstract:Recently, Optimistic Multiplicative Weights Update (OMWU) was proven to be the first constant step-size algorithm in the online no-regret framework to enjoy last-iterate convergence to Nash Equilibria in the constrained zero-sum bimatrix case, where weights represent the probabilities of playing pure strategies. We introduce the second such algorithm, \textit{Consensus MWU}, for which we prove local convergence and show empirically that it enjoys faster and more robust convergence than OMWU. Our algorithm shows the importance of a new object, the \textit{simplex Hessian}, as well as of the interaction of the game with the (eigen)space of vectors summing to zero, which we believe future research can build on. As for OMWU, CMWU has convergence guarantees in the zero-sum case only, but Cheung and Piliouras (2020) recently showed that OMWU and MWU display opposite convergence properties depending on whether the game is zero-sum or cooperative. Inspired by this work and the recent literature on learning to optimize for single functions, we extend CMWU to non zero-sum games by introducing a new framework for online learning in games, where the update rule's gradient and Hessian coefficients along a trajectory are learnt by a reinforcement learning policy that is conditioned on the nature of the game: \textit{the game signature}. We construct the latter using a new canonical decomposition of two-player games into eight components corresponding to commutative projection operators, generalizing and unifying recent game concepts studied in the literature. We show empirically that our new learning policy is able to exploit the game signature across a wide range of game types.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge