A Neural RDE approach for continuous-time non-Markovian stochastic control problems

We propose a novel framework for solving continuous-time non-Markovian stochastic control problems by means of neural rough differential equations (Neural RDEs) introduced in Morrill et al. (2021). Non-Markovianity naturally arises in control problems due to the time delay effects in the system coefficients or the driving noises, which leads to optimal control strategies depending explicitly on the historical trajectories of the system state. By modelling the control process as the solution of a Neural RDE driven by the state process, we show that the control-state joint dynamics are governed by an uncontrolled, augmented Neural RDE, allowing for fast Monte-Carlo estimation of the value function via trajectories simulation and memory-efficient backpropagation. We provide theoretical underpinnings for the proposed algorithmic framework by demonstrating that Neural RDEs serve as universal approximators for functions of random rough paths. Exhaustive numerical experiments on non-Markovian stochastic control problems are presented, which reveal that the proposed framework is time-resolution-invariant and achieves higher accuracy and better stability in irregular sampling compared to existing RNN-based approaches.

Model-based gym environments for limit order book trading

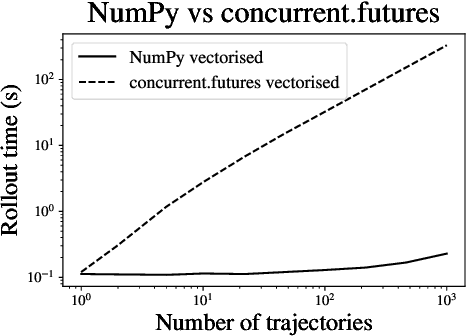
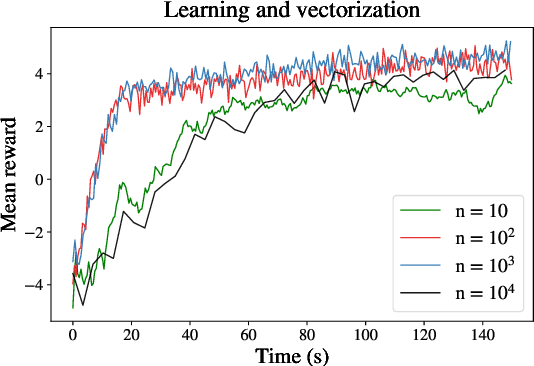
Within the mathematical finance literature there is a rich catalogue of mathematical models for studying algorithmic trading problems -- such as market-making and optimal execution -- in limit order books. This paper introduces \mbtgym, a Python module that provides a suite of gym environments for training reinforcement learning (RL) agents to solve such model-based trading problems. The module is set up in an extensible way to allow the combination of different aspects of different models. It supports highly efficient implementations of vectorized environments to allow faster training of RL agents. In this paper, we motivate the challenge of using RL to solve such model-based limit order book problems in mathematical finance, we explain the design of our gym environment, and then demonstrate its use in solving standard and non-standard problems from the literature. Finally, we lay out a roadmap for further development of our module, which we provide as an open source repository on GitHub so that it can serve as a focal point for RL research in model-based algorithmic trading.