Consensus Multiplicative Weights Update: Learning to Learn using Projector-based Game Signatures

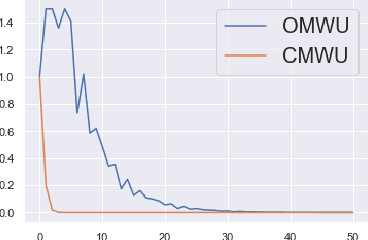
Recently, Optimistic Multiplicative Weights Update (OMWU) was proven to be the first constant step-size algorithm in the online no-regret framework to enjoy last-iterate convergence to Nash Equilibria in the constrained zero-sum bimatrix case, where weights represent the probabilities of playing pure strategies. We introduce the second such algorithm, \textit{Consensus MWU}, for which we prove local convergence and show empirically that it enjoys faster and more robust convergence than OMWU. Our algorithm shows the importance of a new object, the \textit{simplex Hessian}, as well as of the interaction of the game with the (eigen)space of vectors summing to zero, which we believe future research can build on. As for OMWU, CMWU has convergence guarantees in the zero-sum case only, but Cheung and Piliouras (2020) recently showed that OMWU and MWU display opposite convergence properties depending on whether the game is zero-sum or cooperative. Inspired by this work and the recent literature on learning to optimize for single functions, we extend CMWU to non zero-sum games by introducing a new framework for online learning in games, where the update rule's gradient and Hessian coefficients along a trajectory are learnt by a reinforcement learning policy that is conditioned on the nature of the game: \textit{the game signature}. We construct the latter using a new canonical decomposition of two-player games into eight components corresponding to commutative projection operators, generalizing and unifying recent game concepts studied in the literature. We show empirically that our new learning policy is able to exploit the game signature across a wide range of game types.