Assessing data-driven predictions of band gap and electrical conductivity for transparent conducting materials

Machine Learning (ML) has offered innovative perspectives for accelerating the discovery of new functional materials, leveraging the increasing availability of material databases. Despite the promising advances, data-driven methods face constraints imposed by the quantity and quality of available data. Moreover, ML is often employed in tandem with simulated datasets originating from density functional theory (DFT), and assessed through in-sample evaluation schemes. This scenario raises questions about the practical utility of ML in uncovering new and significant material classes for industrial applications. Here, we propose a data-driven framework aimed at accelerating the discovery of new transparent conducting materials (TCMs), an important category of semiconductors with a wide range of applications. To mitigate the shortage of available data, we create and validate unique experimental databases, comprising several examples of existing TCMs. We assess state-of-the-art (SOTA) ML models for property prediction from the stoichiometry alone. We propose a bespoke evaluation scheme to provide empirical evidence on the ability of ML to uncover new, previously unseen materials of interest. We test our approach on a list of 55 compositions containing typical elements of known TCMs. Although our study indicates that ML tends to identify new TCMs compositionally similar to those in the training data, we empirically demonstrate that it can highlight material candidates that may have been previously overlooked, offering a systematic approach to identify materials that are likely to display TCMs characteristics.

Cluster Exploration using Informative Manifold Projections

Dimensionality reduction (DR) is one of the key tools for the visual exploration of high-dimensional data and uncovering its cluster structure in two- or three-dimensional spaces. The vast majority of DR methods in the literature do not take into account any prior knowledge a practitioner may have regarding the dataset under consideration. We propose a novel method to generate informative embeddings which not only factor out the structure associated with different kinds of prior knowledge but also aim to reveal any remaining underlying structure. To achieve this, we employ a linear combination of two objectives: firstly, contrastive PCA that discounts the structure associated with the prior information, and secondly, kurtosis projection pursuit which ensures meaningful data separation in the obtained embeddings. We formulate this task as a manifold optimization problem and validate it empirically across a variety of datasets considering three distinct types of prior knowledge. Lastly, we provide an automated framework to perform iterative visual exploration of high-dimensional data.

EgPDE-Net: Building Continuous Neural Networks for Time Series Prediction with Exogenous Variables

While exogenous variables have a major impact on performance improvement in time series analysis, inter-series correlation and time dependence among them are rarely considered in the present continuous methods. The dynamical systems of multivariate time series could be modelled with complex unknown partial differential equations (PDEs) which play a prominent role in many disciplines of science and engineering. In this paper, we propose a continuous-time model for arbitrary-step prediction to learn an unknown PDE system in multivariate time series whose governing equations are parameterised by self-attention and gated recurrent neural networks. The proposed model, \underline{E}xogenous-\underline{g}uided \underline{P}artial \underline{D}ifferential \underline{E}quation Network (EgPDE-Net), takes account of the relationships among the exogenous variables and their effects on the target series. Importantly, the model can be reduced into a regularised ordinary differential equation (ODE) problem with special designed regularisation guidance, which makes the PDE problem tractable to obtain numerical solutions and feasible to predict multiple future values of the target series at arbitrary time points. Extensive experiments demonstrate that our proposed model could achieve competitive accuracy over strong baselines: on average, it outperforms the best baseline by reducing $9.85\%$ on RMSE and $13.98\%$ on MAE for arbitrary-step prediction.

Entropic trust region for densest crystallographic symmetry group packings

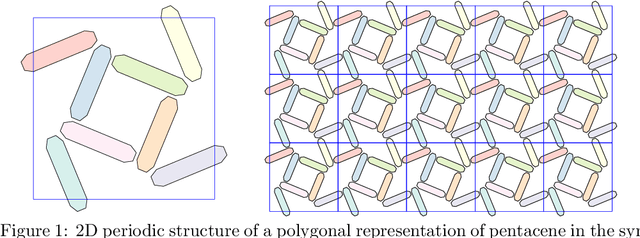
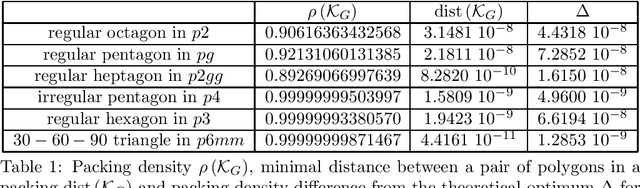
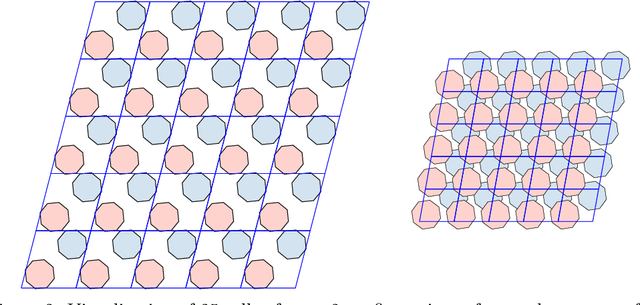
Molecular crystal structure prediction (CSP) seeks the most stable periodic structure given a chemical composition of a molecule and pressure-temperature conditions. Modern CSP solvers use global optimization methods to search for structures with minimal free energy within a complex energy landscape induced by intermolecular potentials. A major caveat of these methods is that initial configurations are random, making thus the search susceptible to the convergence at local minima. Providing initial configurations that are densely packed with respect to the geometric representation of a molecule can significantly accelerate CSP. Motivated by these observations we define a class of periodic packings restricted to crystallographic symmetry groups (CSG) and design a search method for densest CSG packings in an information geometric framework. Since the CSG induce a toroidal topology on the configuration space, a non-euclidean trust region method is performed on a statistical manifold consisting of probability distributions defined on an $n$-dimensional flat unit torus by extending the multivariate von Mises distribution. By introducing an adaptive quantile reformulation of the fitness function into the optimization schedule we provide the algorithm a geometric characterization through local dual geodesic flows. Moreover, we examine the geometry of the adaptive selection quantile defined trust region and show that the algorithm performs a maximization of stochastic dependence among elements of the extended multivariate von Mises distributed random vector. We experimentally evaluate its behavior and performance on various densest packings of convex polygons in $2$-dimensional CSG for which optimal solutions are known.

Discriminative Triad Matching and Reconstruction for Weakly Referring Expression Grounding

In this paper, we are tackling the weakly-supervised referring expression grounding task, for the localization of a referent object in an image according to a query sentence, where the mapping between image regions and queries are not available during the training stage. In traditional methods, an object region that best matches the referring expression is picked out, and then the query sentence is reconstructed from the selected region, where the reconstruction difference serves as the loss for back-propagation. The existing methods, however, conduct both the matching and the reconstruction approximately as they ignore the fact that the matching correctness is unknown. To overcome this limitation, a discriminative triad is designed here as the basis to the solution, through which a query can be converted into one or multiple discriminative triads in a very scalable way. Based on the discriminative triad, we further propose the triad-level matching and reconstruction modules which are lightweight yet effective for the weakly-supervised training, making it three times lighter and faster than the previous state-of-the-art methods. One important merit of our work is its superior performance despite the simple and neat design. Specifically, the proposed method achieves a new state-of-the-art accuracy when evaluated on RefCOCO (39.21%), RefCOCO+ (39.18%) and RefCOCOg (43.24%) datasets, that is 4.17%, 4.08% and 7.8% higher than the previous one, respectively.