Accelerating Material Property Prediction using Generically Complete Isometry Invariants

Material or crystal property prediction using machine learning has grown popular in recent years as it provides a computationally efficient replacement to classical simulation methods. A crucial first step for any of these algorithms is the representation used for a periodic crystal. While similar objects like molecules and proteins have a finite number of atoms and their representation can be built based upon a finite point cloud interpretation, periodic crystals are unbounded in size, making their representation more challenging. In the present work, we adapt the Pointwise Distance Distribution (PDD), a continuous and generically complete isometry invariant for periodic point sets, as a representation for our learning algorithm. While the PDD is effective in distinguishing periodic point sets up to isometry, there is no consideration for the composition of the underlying material. We develop a transformer model with a modified self-attention mechanism that can utilize the PDD and incorporate compositional information via a spatial encoding method. This model is tested on the crystals of the Materials Project and Jarvis-DFT databases and shown to produce accuracy on par with state-of-the-art methods while being several times faster in both training and prediction time.

Recognizing Rigid Patterns of Unlabeled Point Clouds by Complete and Continuous Isometry Invariants with no False Negatives and no False Positives

Rigid structures such as cars or any other solid objects are often represented by finite clouds of unlabeled points. The most natural equivalence on these point clouds is rigid motion or isometry maintaining all inter-point distances. Rigid patterns of point clouds can be reliably compared only by complete isometry invariants that can also be called equivariant descriptors without false negatives (isometric clouds having different descriptions) and without false positives (non-isometric clouds with the same description). Noise and motion in data motivate a search for invariants that are continuous under perturbations of points in a suitable metric. We propose the first continuous and complete invariant of unlabeled clouds in any Euclidean space. For a fixed dimension, the new metric for this invariant is computable in a polynomial time in the number of points.

Compact Graph Representation of molecular crystals using Point-wise Distance Distributions

Use of graphs to represent molecular crystals has become popular in recent years as they provide a natural translation from atoms and bonds to nodes and edges. Graphs capture structure, while remaining invariant to the symmetries that crystals display. Several works in property prediction, including those with state-of-the-art results, make use of the Crystal Graph. The present work offers a graph based on Point-wise Distance Distributions which retains symmetrical invariance, decreases computational load, and yields similar or better prediction accuracy on both experimental and simulated crystals.

Entropic trust region for densest crystallographic symmetry group packings

Molecular crystal structure prediction (CSP) seeks the most stable periodic structure given a chemical composition of a molecule and pressure-temperature conditions. Modern CSP solvers use global optimization methods to search for structures with minimal free energy within a complex energy landscape induced by intermolecular potentials. A major caveat of these methods is that initial configurations are random, making thus the search susceptible to the convergence at local minima. Providing initial configurations that are densely packed with respect to the geometric representation of a molecule can significantly accelerate CSP. Motivated by these observations we define a class of periodic packings restricted to crystallographic symmetry groups (CSG) and design a search method for densest CSG packings in an information geometric framework. Since the CSG induce a toroidal topology on the configuration space, a non-euclidean trust region method is performed on a statistical manifold consisting of probability distributions defined on an $n$-dimensional flat unit torus by extending the multivariate von Mises distribution. By introducing an adaptive quantile reformulation of the fitness function into the optimization schedule we provide the algorithm a geometric characterization through local dual geodesic flows. Moreover, we examine the geometry of the adaptive selection quantile defined trust region and show that the algorithm performs a maximization of stochastic dependence among elements of the extended multivariate von Mises distributed random vector. We experimentally evaluate its behavior and performance on various densest packings of convex polygons in $2$-dimensional CSG for which optimal solutions are known.

Fast predictions of lattice energies by continuous isometry invariants of crystal structures

Crystal Structure Prediction (CSP) aims to discover solid crystalline materials by optimizing periodic arrangements of atoms, ions or molecules. CSP takes weeks of supercomputer time because of slow energy minimizations for millions of simulated crystals. The lattice energy is a key physical property, which determines thermodynamic stability of a crystal but has no simple analytic expression. Past machine learning approaches to predict the lattice energy used slow crystal descriptors depending on manually chosen parameters. The new area of Periodic Geometry offers much faster isometry invariants that are also continuous under perturbations of atoms. Our experiments on simulated crystals confirm that a small distance between the new invariants guarantees a small difference of energies. We compare several kernel methods for invariant-based predictions of energy and achieve the mean absolute error of less than 5kJ/mole or 0.05eV/atom on a dataset of 5679 crystals.

Resolution-independent meshes of super pixels

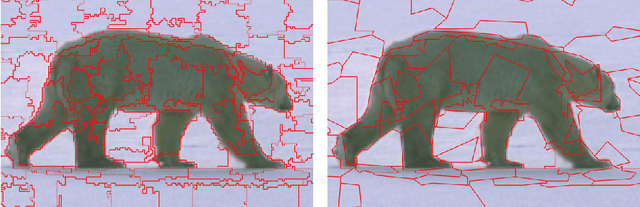
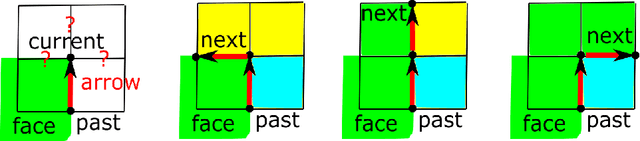
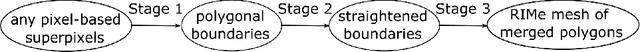
The over-segmentation into superpixels is an important preprocessing step to smartly compress the input size and speed up higher level tasks. A superpixel was traditionally considered as a small cluster of square-based pixels that have similar color intensities and are closely located to each other. In this discrete model the boundaries of superpixels often have irregular zigzags consisting of horizontal or vertical edges from a given pixel grid. However digital images represent a continuous world, hence the following continuous model in the resolution-independent formulation can be more suitable for the reconstruction problem. Instead of uniting squares in a grid, a resolution-independent superpixel is defined as a polygon that has straight edges with any possible slope at subpixel resolution. The harder continuous version of the over-segmentation problem is to split an image into polygons and find a best (say, constant) color of each polygon so that the resulting colored mesh well approximates the given image. Such a mesh of polygons can be rendered at any higher resolution with all edges kept straight. We propose a fast conversion of any traditional superpixels into polygons and guarantees that their straight edges do not intersect. The meshes based on the superpixels SEEDS (Superpixels Extracted via Energy-Driven Sampling) and SLIC (Simple Linear Iterative Clustering) are compared with past meshes based on the Line Segment Detector. The experiments on the Berkeley Segmentation Database confirm that the new superpixels have more compact shapes than pixel-based superpixels.

Approximating persistent homology for a cloud of $n$ points in a subquadratic time

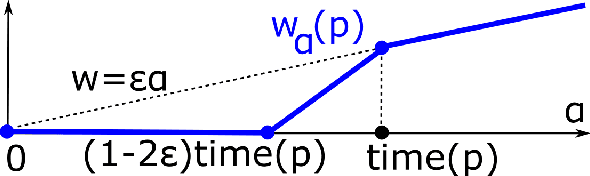
The Vietoris-Rips filtration for an $n$-point metric space is a sequence of large simplicial complexes adding a topological structure to the otherwise disconnected space. The persistent homology is a key tool in topological data analysis and studies topological features of data that persist over many scales. The fastest algorithm for computing persistent homology of a filtration has time $O(M(u)+u^2\log^2 u)$, where $u$ is the number of updates (additions or deletions of simplices), $M(u)=O(u^{2.376})$ is the time for multiplication of $u\times u$ matrices. For a space of $n$ points given by their pairwise distances, we approximate the Vietoris-Rips filtration by a zigzag filtration consisting of $u=o(n)$ updates, which is sublinear in $n$. The constant depends on a given error of approximation and on the doubling dimension of the metric space. Then the persistent homology of this sublinear-size filtration can be computed in time $o(n^2)$, which is subquadratic in $n$.

A fast and robust algorithm to count topologically persistent holes in noisy clouds

Preprocessing a 2D image often produces a noisy cloud of interest points. We study the problem of counting holes in unorganized clouds in the plane. The holes in a given cloud are quantified by the topological persistence of their boundary contours when the cloud is analyzed at all possible scales. We design the algorithm to count holes that are most persistent in the filtration of offsets (neighborhoods) around given points. The input is a cloud of $n$ points in the plane without any user-defined parameters. The algorithm has $O(n\log n)$ time and $O(n)$ space. The output is the array (number of holes, relative persistence in the filtration). We prove theoretical guarantees when the algorithm finds the correct number of holes (components in the complement) of an unknown shape approximated by a cloud.

Book embeddings of Reeb graphs

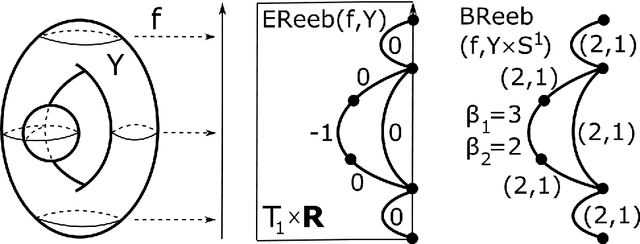
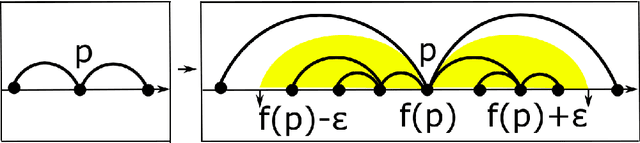
Let $X$ be a simplicial complex with a piecewise linear function $f:X\to\mathbb{R}$. The Reeb graph $Reeb(f,X)$ is the quotient of $X$, where we collapse each connected component of $f^{-1}(t)$ to a single point. Let the nodes of $Reeb(f,X)$ be all homologically critical points where any homology of the corresponding component of the level set $f^{-1}(t)$ changes. Then we can label every arc of $Reeb(f,X)$ with the Betti numbers $(\beta_1,\beta_2,\dots,\beta_d)$ of the corresponding $d$-dimensional component of a level set. The homology labels give more information about the original complex $X$ than the classical Reeb graph. We describe a canonical embedding of a Reeb graph into a multi-page book (a star cross a line) and give a unique linear code of this book embedding.