Fast predictions of lattice energies by continuous isometry invariants of crystal structures
Paper and Code
Aug 11, 2021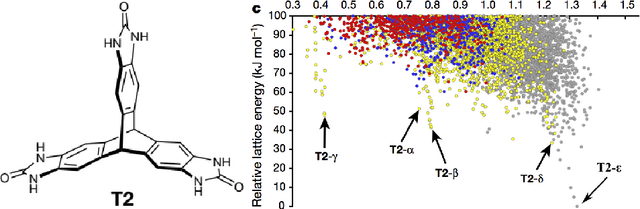
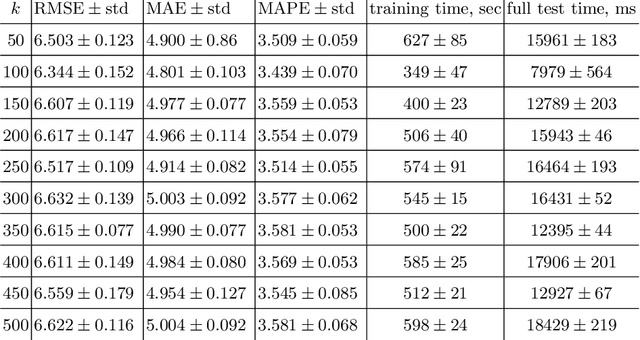
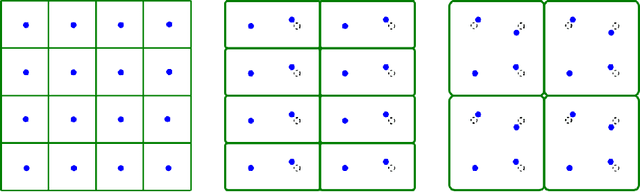

Crystal Structure Prediction (CSP) aims to discover solid crystalline materials by optimizing periodic arrangements of atoms, ions or molecules. CSP takes weeks of supercomputer time because of slow energy minimizations for millions of simulated crystals. The lattice energy is a key physical property, which determines thermodynamic stability of a crystal but has no simple analytic expression. Past machine learning approaches to predict the lattice energy used slow crystal descriptors depending on manually chosen parameters. The new area of Periodic Geometry offers much faster isometry invariants that are also continuous under perturbations of atoms. Our experiments on simulated crystals confirm that a small distance between the new invariants guarantees a small difference of energies. We compare several kernel methods for invariant-based predictions of energy and achieve the mean absolute error of less than 5kJ/mole or 0.05eV/atom on a dataset of 5679 crystals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge