Resolution-independent meshes of super pixels
Paper and Code
Nov 01, 2019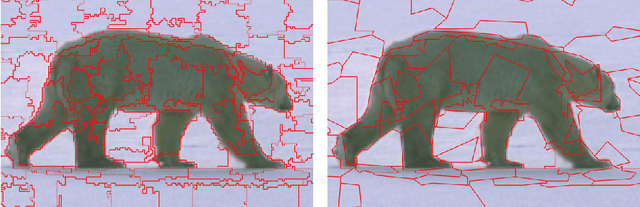

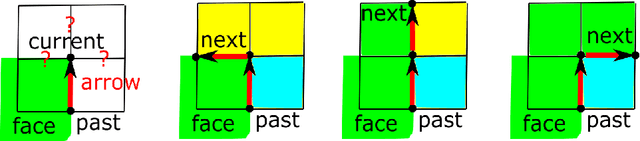
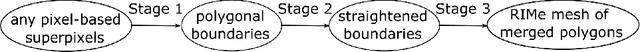
The over-segmentation into superpixels is an important preprocessing step to smartly compress the input size and speed up higher level tasks. A superpixel was traditionally considered as a small cluster of square-based pixels that have similar color intensities and are closely located to each other. In this discrete model the boundaries of superpixels often have irregular zigzags consisting of horizontal or vertical edges from a given pixel grid. However digital images represent a continuous world, hence the following continuous model in the resolution-independent formulation can be more suitable for the reconstruction problem. Instead of uniting squares in a grid, a resolution-independent superpixel is defined as a polygon that has straight edges with any possible slope at subpixel resolution. The harder continuous version of the over-segmentation problem is to split an image into polygons and find a best (say, constant) color of each polygon so that the resulting colored mesh well approximates the given image. Such a mesh of polygons can be rendered at any higher resolution with all edges kept straight. We propose a fast conversion of any traditional superpixels into polygons and guarantees that their straight edges do not intersect. The meshes based on the superpixels SEEDS (Superpixels Extracted via Energy-Driven Sampling) and SLIC (Simple Linear Iterative Clustering) are compared with past meshes based on the Line Segment Detector. The experiments on the Berkeley Segmentation Database confirm that the new superpixels have more compact shapes than pixel-based superpixels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge