Entropic trust region for densest crystallographic symmetry group packings

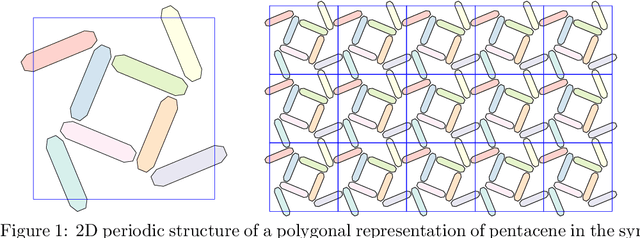
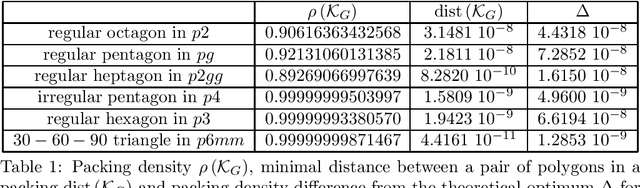
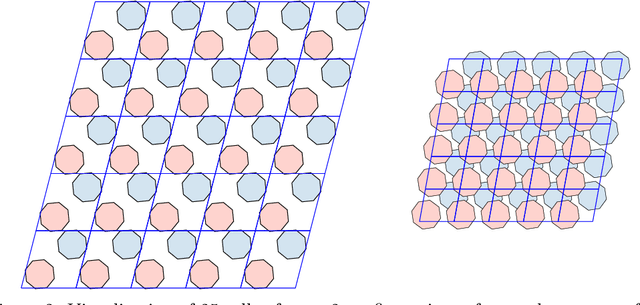
Molecular crystal structure prediction (CSP) seeks the most stable periodic structure given a chemical composition of a molecule and pressure-temperature conditions. Modern CSP solvers use global optimization methods to search for structures with minimal free energy within a complex energy landscape induced by intermolecular potentials. A major caveat of these methods is that initial configurations are random, making thus the search susceptible to the convergence at local minima. Providing initial configurations that are densely packed with respect to the geometric representation of a molecule can significantly accelerate CSP. Motivated by these observations we define a class of periodic packings restricted to crystallographic symmetry groups (CSG) and design a search method for densest CSG packings in an information geometric framework. Since the CSG induce a toroidal topology on the configuration space, a non-euclidean trust region method is performed on a statistical manifold consisting of probability distributions defined on an $n$-dimensional flat unit torus by extending the multivariate von Mises distribution. By introducing an adaptive quantile reformulation of the fitness function into the optimization schedule we provide the algorithm a geometric characterization through local dual geodesic flows. Moreover, we examine the geometry of the adaptive selection quantile defined trust region and show that the algorithm performs a maximization of stochastic dependence among elements of the extended multivariate von Mises distributed random vector. We experimentally evaluate its behavior and performance on various densest packings of convex polygons in $2$-dimensional CSG for which optimal solutions are known.