Assessing data-driven predictions of band gap and electrical conductivity for transparent conducting materials

Machine Learning (ML) has offered innovative perspectives for accelerating the discovery of new functional materials, leveraging the increasing availability of material databases. Despite the promising advances, data-driven methods face constraints imposed by the quantity and quality of available data. Moreover, ML is often employed in tandem with simulated datasets originating from density functional theory (DFT), and assessed through in-sample evaluation schemes. This scenario raises questions about the practical utility of ML in uncovering new and significant material classes for industrial applications. Here, we propose a data-driven framework aimed at accelerating the discovery of new transparent conducting materials (TCMs), an important category of semiconductors with a wide range of applications. To mitigate the shortage of available data, we create and validate unique experimental databases, comprising several examples of existing TCMs. We assess state-of-the-art (SOTA) ML models for property prediction from the stoichiometry alone. We propose a bespoke evaluation scheme to provide empirical evidence on the ability of ML to uncover new, previously unseen materials of interest. We test our approach on a list of 55 compositions containing typical elements of known TCMs. Although our study indicates that ML tends to identify new TCMs compositionally similar to those in the training data, we empirically demonstrate that it can highlight material candidates that may have been previously overlooked, offering a systematic approach to identify materials that are likely to display TCMs characteristics.

Cluster Exploration using Informative Manifold Projections

Dimensionality reduction (DR) is one of the key tools for the visual exploration of high-dimensional data and uncovering its cluster structure in two- or three-dimensional spaces. The vast majority of DR methods in the literature do not take into account any prior knowledge a practitioner may have regarding the dataset under consideration. We propose a novel method to generate informative embeddings which not only factor out the structure associated with different kinds of prior knowledge but also aim to reveal any remaining underlying structure. To achieve this, we employ a linear combination of two objectives: firstly, contrastive PCA that discounts the structure associated with the prior information, and secondly, kurtosis projection pursuit which ensures meaningful data separation in the obtained embeddings. We formulate this task as a manifold optimization problem and validate it empirically across a variety of datasets considering three distinct types of prior knowledge. Lastly, we provide an automated framework to perform iterative visual exploration of high-dimensional data.

Metrics for quantifying isotropy in high dimensional unsupervised clustering tasks in a materials context

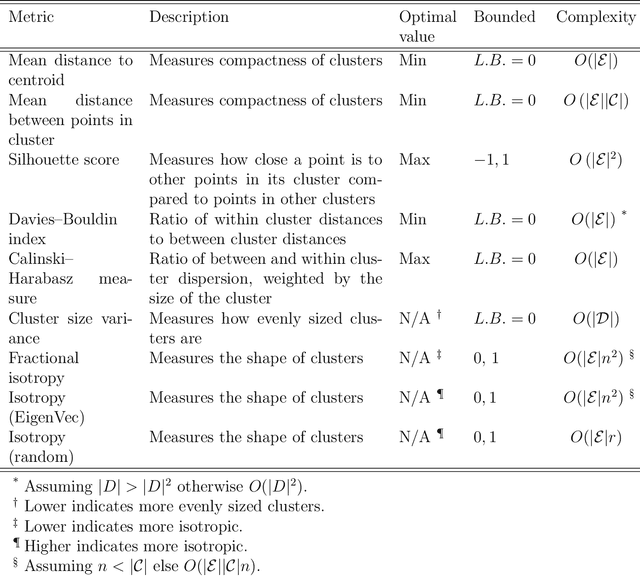
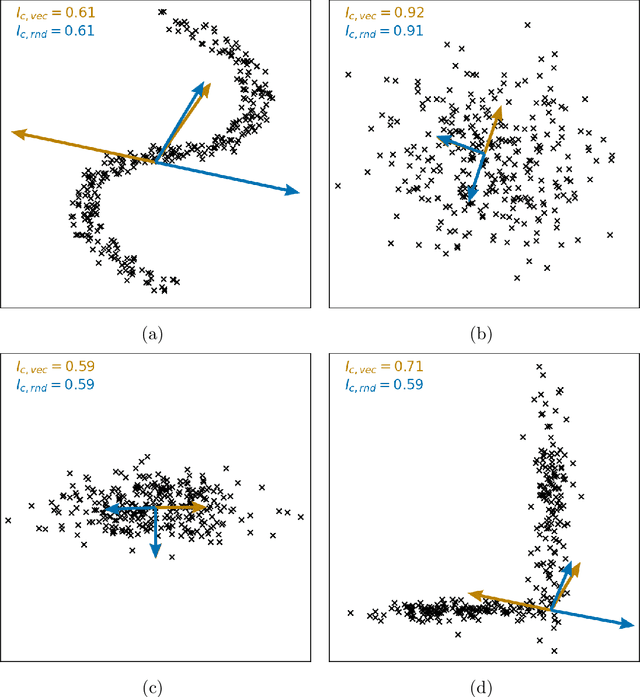
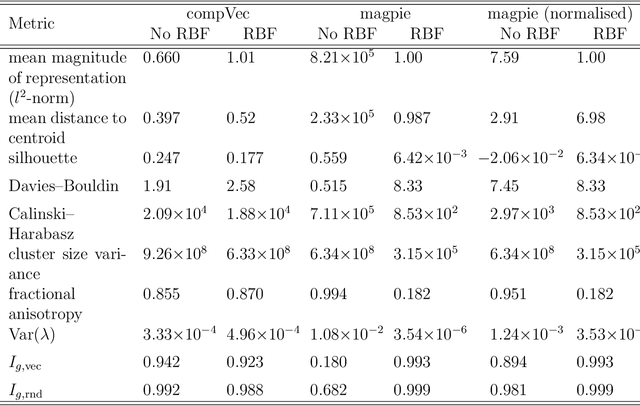
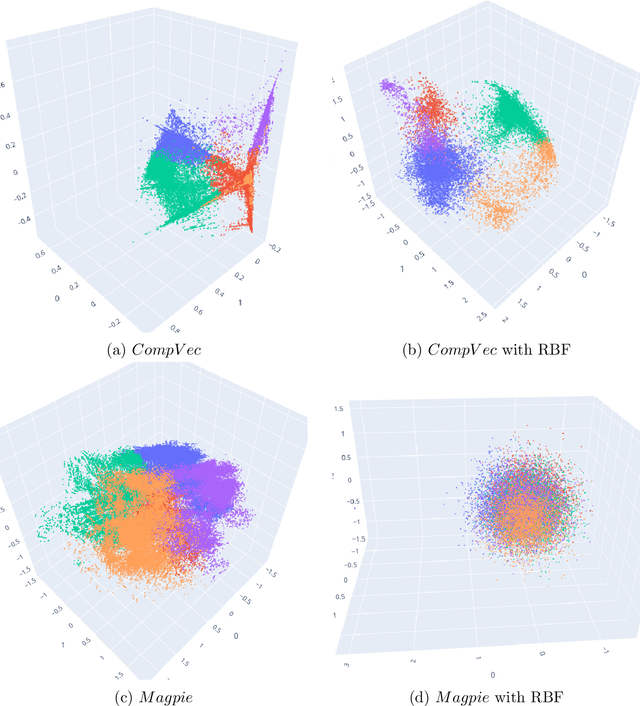
Clustering is a common task in machine learning, but clusters of unlabelled data can be hard to quantify. The application of clustering algorithms in chemistry is often dependant on material representation. Ascertaining the effects of different representations, clustering algorithms, or data transformations on the resulting clusters is difficult due to the dimensionality of these data. We present a thorough analysis of measures for isotropy of a cluster, including a novel implantation based on an existing derivation. Using fractional anisotropy, a common method used in medical imaging for comparison, we then expand these measures to examine the average isotropy of a set of clusters. A use case for such measures is demonstrated by quantifying the effects of kernel approximation functions on different representations of the Inorganic Crystal Structure Database. Broader applicability of these methods is demonstrated in analysing learnt embedding of the MNIST dataset. Random clusters are explored to examine the differences between isotropy measures presented, and to see how each method scales with the dimensionality. Python implementations of these measures are provided for use by the community.

Random projections and Kernelised Leave One Cluster Out Cross-Validation: Universal baselines and evaluation tools for supervised machine learning for materials properties

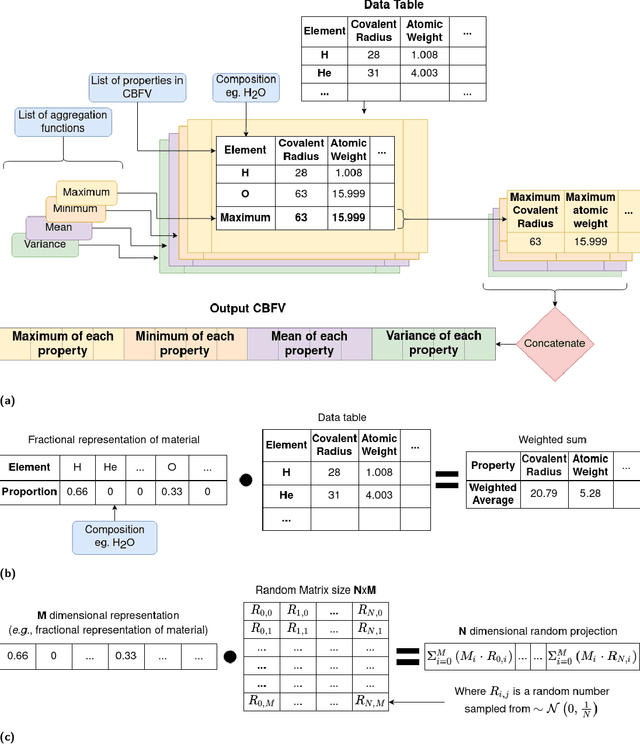
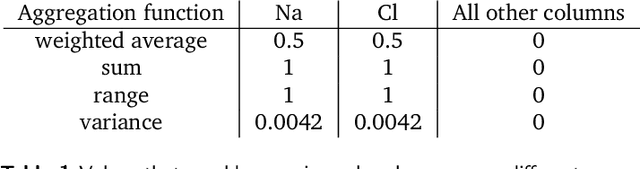
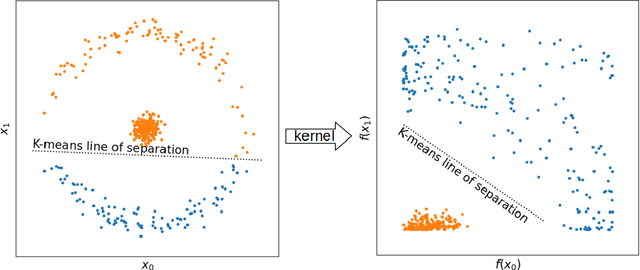
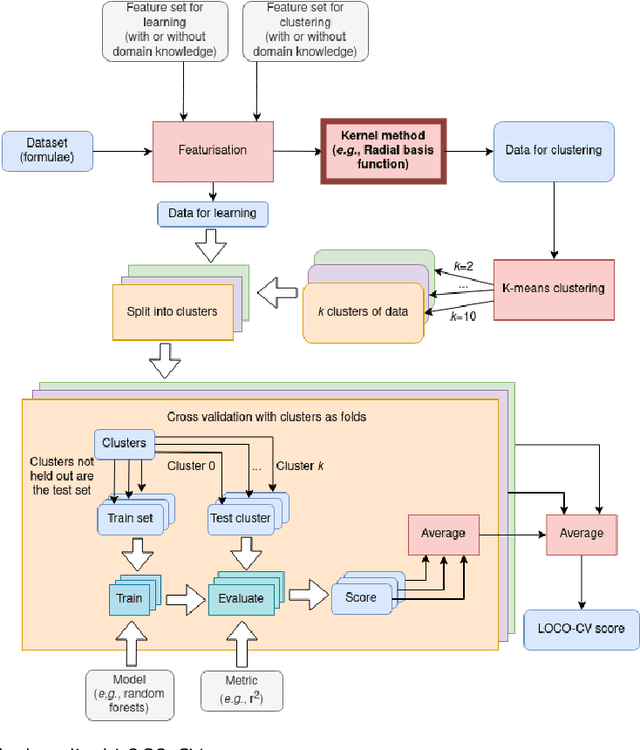
With machine learning being a popular topic in current computational materials science literature, creating representations for compounds has become common place. These representations are rarely compared, as evaluating their performance - and the performance of the algorithms that they are used with - is non-trivial. With many materials datasets containing bias and skew caused by the research process, leave one cluster out cross validation (LOCO-CV) has been introduced as a way of measuring the performance of an algorithm in predicting previously unseen groups of materials. This raises the question of the impact, and control, of the range of cluster sizes on the LOCO-CV measurement outcomes. We present a thorough comparison between composition-based representations, and investigate how kernel approximation functions can be used to better separate data to enhance LOCO-CV applications. We find that domain knowledge does not improve machine learning performance in most tasks tested, with band gap prediction being the notable exception. We also find that the radial basis function improves the linear separability of chemical datasets in all 10 datasets tested and provide a framework for the application of this function in the LOCO-CV process to improve the outcome of LOCO-CV measurements regardless of machine learning algorithm, choice of metric, and choice of compound representation. We recommend kernelised LOCO-CV as a training paradigm for those looking to measure the extrapolatory power of an algorithm on materials data.

Element selection for functional materials discovery by integrated machine learning of atomic contributions to properties

At the high level, the fundamental differences between materials originate from the unique nature of the constituent chemical elements. Before specific differences emerge according to the precise ratios of elements (composition) in a given crystal structure (phase), the material can be represented by its phase field defined simply as the set of the constituent chemical elements. Classification of the materials at the level of their phase fields can accelerate materials discovery by selecting the elemental combinations that are likely to produce desirable functional properties in synthetically accessible materials. Here, we demonstrate that classification of the materials phase field with respect to the maximum expected value of a target functional property can be combined with the ranking of the materials synthetic accessibility. This end-to-end machine learning approach (PhaseSelect) first derives the atomic characteristics from the compositional environments in all computationally and experimentally explored materials and then employs these characteristics to classify the phase field by their merit. PhaseSelect can quantify the materials potential at the level of the periodic table, which we demonstrate with significant accuracy for three avenues of materials applications: high-temperature superconducting, high-temperature magnetic and targetted energy band gap materials.