Metrics for quantifying isotropy in high dimensional unsupervised clustering tasks in a materials context

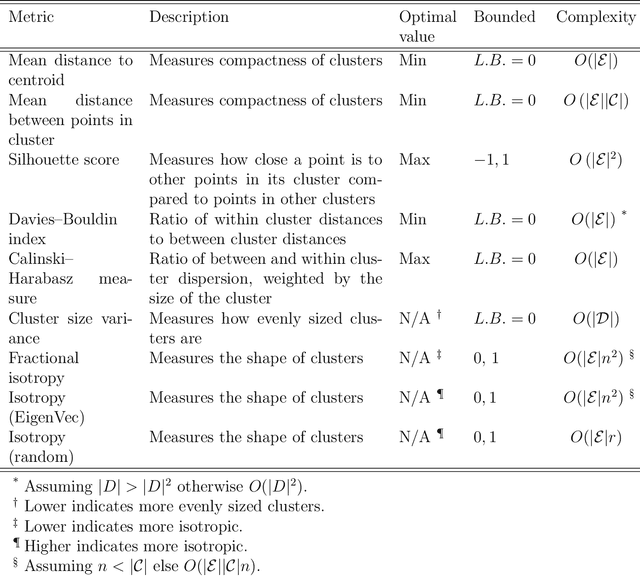
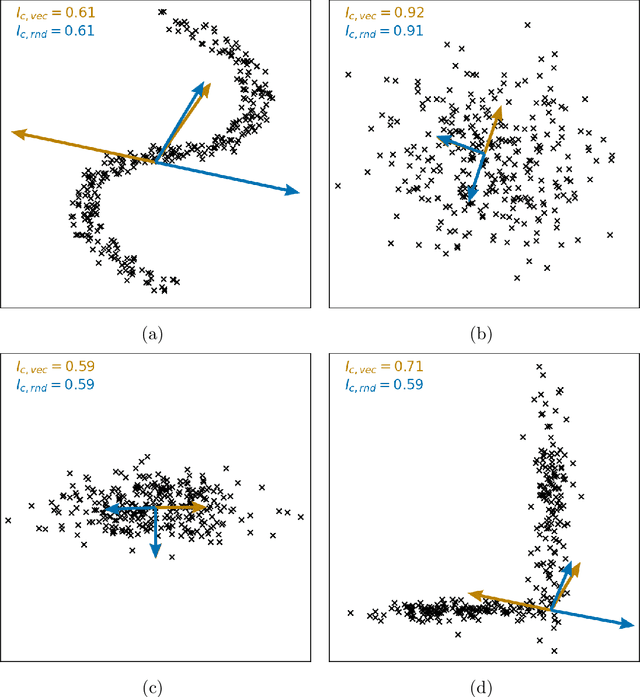
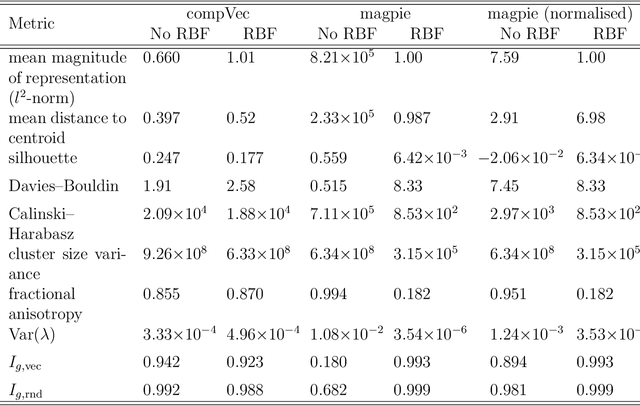
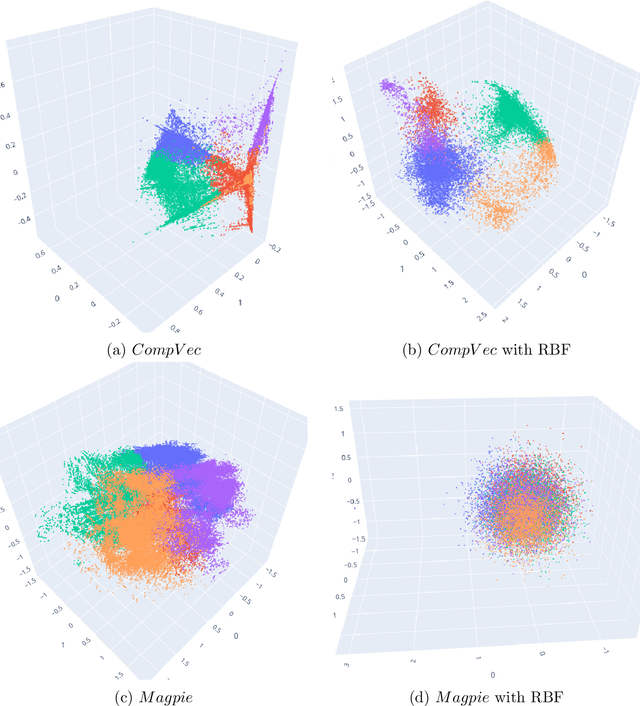
Clustering is a common task in machine learning, but clusters of unlabelled data can be hard to quantify. The application of clustering algorithms in chemistry is often dependant on material representation. Ascertaining the effects of different representations, clustering algorithms, or data transformations on the resulting clusters is difficult due to the dimensionality of these data. We present a thorough analysis of measures for isotropy of a cluster, including a novel implantation based on an existing derivation. Using fractional anisotropy, a common method used in medical imaging for comparison, we then expand these measures to examine the average isotropy of a set of clusters. A use case for such measures is demonstrated by quantifying the effects of kernel approximation functions on different representations of the Inorganic Crystal Structure Database. Broader applicability of these methods is demonstrated in analysing learnt embedding of the MNIST dataset. Random clusters are explored to examine the differences between isotropy measures presented, and to see how each method scales with the dimensionality. Python implementations of these measures are provided for use by the community.

Random projections and Kernelised Leave One Cluster Out Cross-Validation: Universal baselines and evaluation tools for supervised machine learning for materials properties

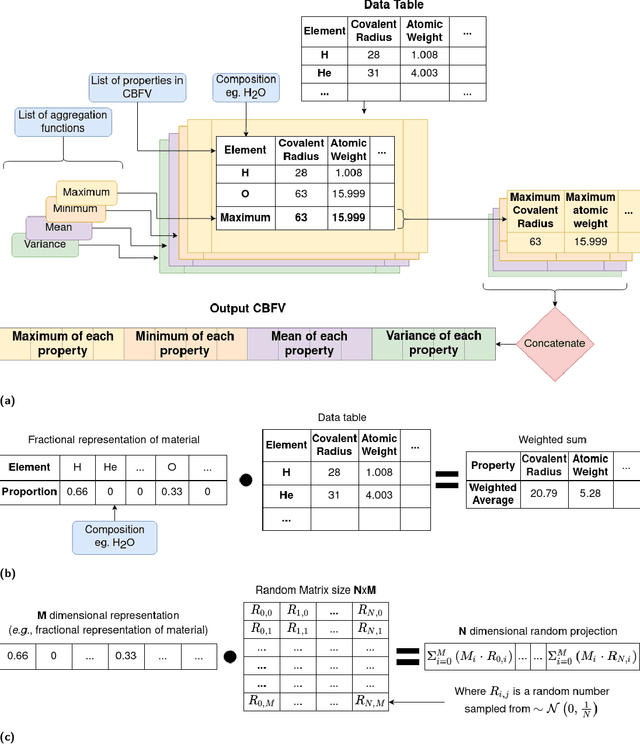
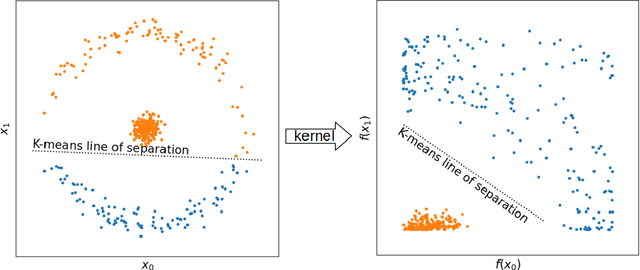
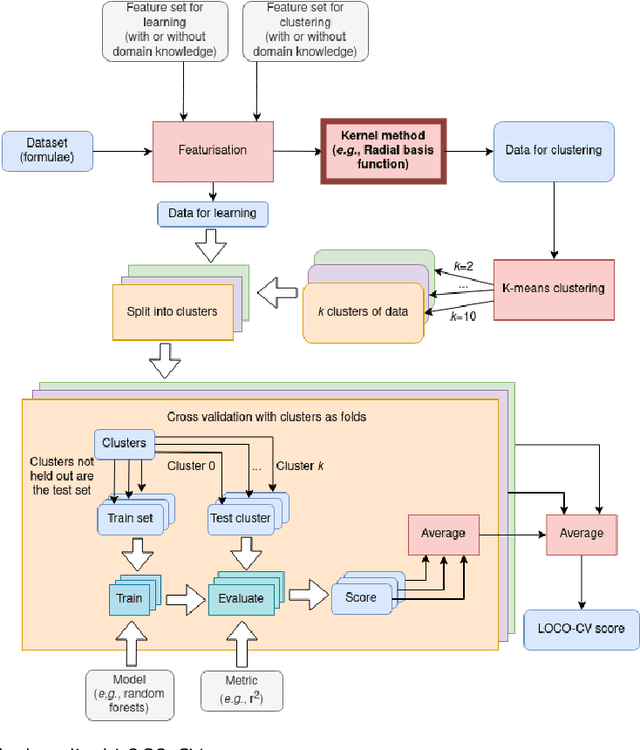
With machine learning being a popular topic in current computational materials science literature, creating representations for compounds has become common place. These representations are rarely compared, as evaluating their performance - and the performance of the algorithms that they are used with - is non-trivial. With many materials datasets containing bias and skew caused by the research process, leave one cluster out cross validation (LOCO-CV) has been introduced as a way of measuring the performance of an algorithm in predicting previously unseen groups of materials. This raises the question of the impact, and control, of the range of cluster sizes on the LOCO-CV measurement outcomes. We present a thorough comparison between composition-based representations, and investigate how kernel approximation functions can be used to better separate data to enhance LOCO-CV applications. We find that domain knowledge does not improve machine learning performance in most tasks tested, with band gap prediction being the notable exception. We also find that the radial basis function improves the linear separability of chemical datasets in all 10 datasets tested and provide a framework for the application of this function in the LOCO-CV process to improve the outcome of LOCO-CV measurements regardless of machine learning algorithm, choice of metric, and choice of compound representation. We recommend kernelised LOCO-CV as a training paradigm for those looking to measure the extrapolatory power of an algorithm on materials data.