Bayesian Decision Trees Inspired from Evolutionary Algorithms

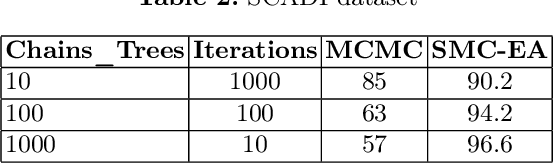
Bayesian Decision Trees (DTs) are generally considered a more advanced and accurate model than a regular Decision Tree (DT) because they can handle complex and uncertain data. Existing work on Bayesian DTs uses Markov Chain Monte Carlo (MCMC) with an accept-reject mechanism and sample using naive proposals to proceed to the next iteration, which can be slow because of the burn-in time needed. We can reduce the burn-in period by proposing a more sophisticated way of sampling or by designing a different numerical Bayesian approach. In this paper, we propose a replacement of the MCMC with an inherently parallel algorithm, the Sequential Monte Carlo (SMC), and a more effective sampling strategy inspired by the Evolutionary Algorithms (EA). Experiments show that SMC combined with the EA can produce more accurate results compared to MCMC in 100 times fewer iterations.

Parallel Approaches to Accelerate Bayesian Decision Trees

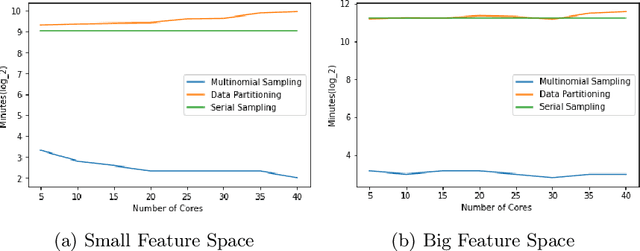
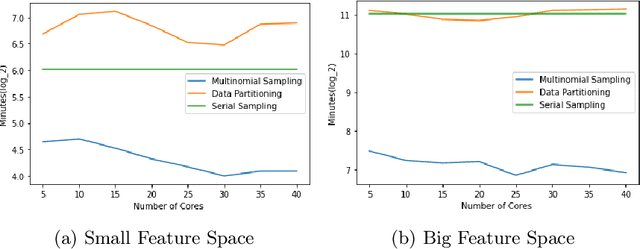
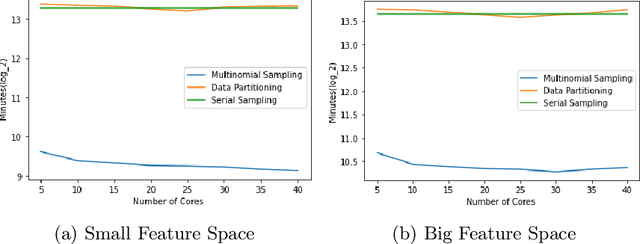
Markov Chain Monte Carlo (MCMC) is a well-established family of algorithms primarily used in Bayesian statistics to sample from a target distribution when direct sampling is challenging. Existing work on Bayesian decision trees uses MCMC. Unfortunately, this can be slow, especially when considering large volumes of data. It is hard to parallelise the accept-reject component of the MCMC. None-the-less, we propose two methods for exploiting parallelism in the MCMC: in the first, we replace the MCMC with another numerical Bayesian approach, the Sequential Monte Carlo (SMC) sampler, which has the appealing property that it is an inherently parallel algorithm; in the second, we consider data partitioning. Both methods use multi-core processing with a HighPerformance Computing (HPC) resource. We test the two methods in various study settings to determine which method is the most beneficial for each test case. Experiments show that data partitioning has limited utility in the settings we consider and that the use of the SMC sampler can improve run-time (compared to the sequential implementation) by up to a factor of 343.

Single MCMC Chain Parallelisation on Decision Trees

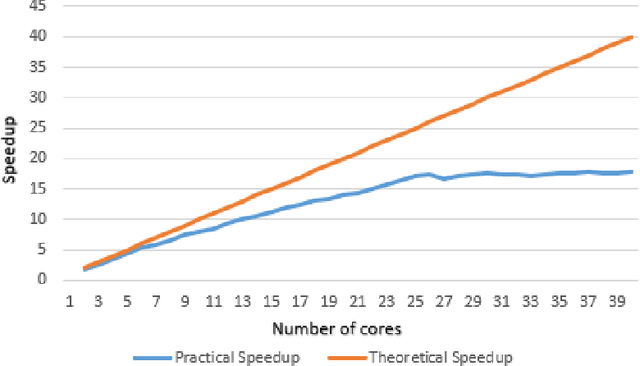
Decision trees are highly famous in machine learning and usually acquire state-of-the-art performance. Despite that, well-known variants like CART, ID3, random forest, and boosted trees miss a probabilistic version that encodes prior assumptions about tree structures and shares statistical strength between node parameters. Existing work on Bayesian decision trees depend on Markov Chain Monte Carlo (MCMC), which can be computationally slow, especially on high dimensional data and expensive proposals. In this study, we propose a method to parallelise a single MCMC decision tree chain on an average laptop or personal computer that enables us to reduce its run-time through multi-core processing while the results are statistically identical to conventional sequential implementation. We also calculate the theoretical and practical reduction in run time, which can be obtained utilising our method on multi-processor architectures. Experiments showed that we could achieve 18 times faster running time provided that the serial and the parallel implementation are statistically identical.

On the Transformation Capability of Feasible Mechanisms for Programmable Matter

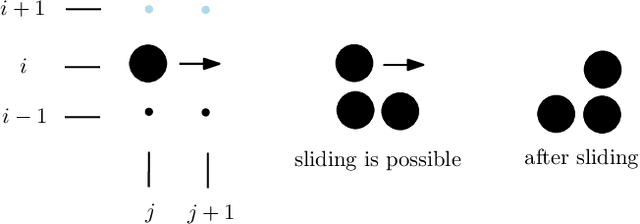
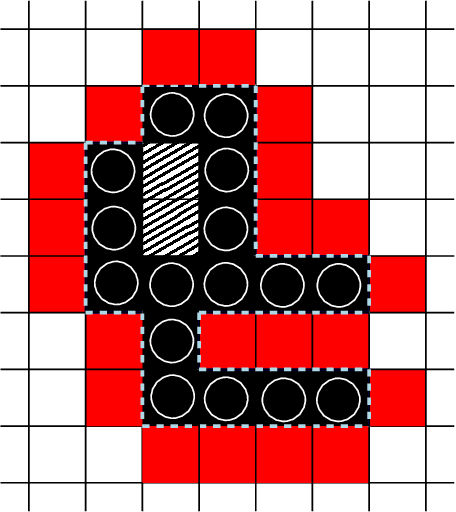
In this work, we study theoretical models of \emph{programmable matter} systems. The systems under consideration consist of spherical modules, kept together by magnetic forces and able to perform two minimal mechanical operations (or movements): \emph{rotate} around a neighbor and \emph{slide} over a line. In terms of modeling, there are $n$ nodes arranged in a 2-dimensional grid and forming some initial \emph{shape}. The goal is for the initial shape $A$ to \emph{transform} to some target shape $B$ by a sequence of movements. Most of the paper focuses on \emph{transformability} questions, meaning whether it is in principle feasible to transform a given shape to another. We first consider the case in which only rotation is available to the nodes. Our main result is that deciding whether two given shapes $A$ and $B$ can be transformed to each other, is in $\mathbf{P}$. We then insist on rotation only and impose the restriction that the nodes must maintain global connectivity throughout the transformation. We prove that the corresponding transformability question is in $\mathbf{PSPACE}$ and study the problem of determining the minimum \emph{seeds} that can make feasible, otherwise infeasible transformations. Next we allow both rotations and slidings and prove universality: any two connected shapes $A,B$ of the same order, can be transformed to each other without breaking connectivity. The worst-case number of movements of the generic strategy is $\Omega(n^2)$. We improve this to $O(n)$ parallel time, by a pipelining strategy, and prove optimality of both by matching lower bounds. In the last part of the paper, we turn our attention to distributed transformations. The nodes are now distributed processes able to perform communicate-compute-move rounds. We provide distributed algorithms for a general type of transformations.