The Maximum Cover with Rotating Field of View

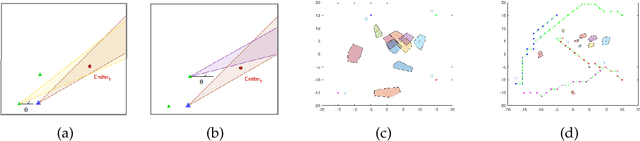
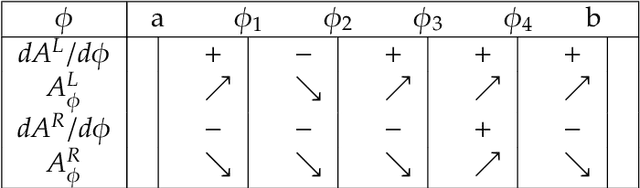
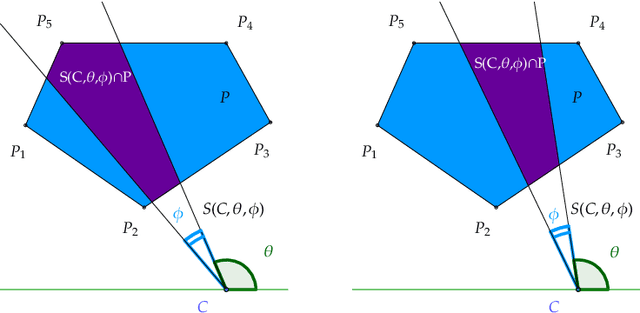
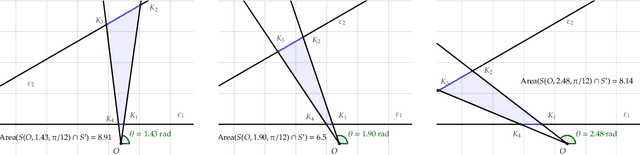
Imagine a polygon-shaped platform $P$ and only one static spotlight outside $P$; which direction should the spotlight face to light most of $P$? This problem occurs in maximising the visibility, as well as in limiting the uncertainty in localisation problems. More formally, we define the following maximum cover problem: "Given a convex polygon $P$ and a Field Of View (FOV) with a given centre and inner angle $\phi$; find the direction (an angle of rotation $\theta$) of the FOV such that the intersection between the FOV and $P$ has the maximum area". In this paper, we provide the theoretical foundation for the analysis of the maximum cover with a rotating field of view. The main challenge is that the function of the area $A_{\phi}(\theta)$, with the angle of rotation $\theta$ and the fixed inner angle $\phi$, cannot be approximated directly. We found an alternative way to express it by various compositions of a function $A_{\theta}(\phi)$ (with a restricted inner angle $\phi$ and a fixed direction $\theta$). We show that $A_{\theta}(\phi)$ has an analytical solution in the special case of a two-sector intersection and later provides a constrictive solution for the original problem. Since the optimal solution is a real number, we develop an algorithm that approximates the direction of the field of view, with precision $\varepsilon$, and complexity $\mathcal{O}(n(\log{n}+(\log{\varepsilon})/\phi))$.

Distributed Transformations of Hamiltonian Shapes based on Line Moves

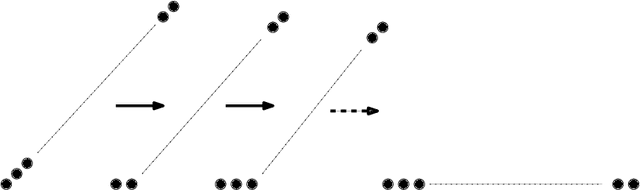
We consider a discrete system of $n$ simple indistinguishable devices, called \emph{agents}, forming a \emph{connected} shape $S_I$ on a two-dimensional square grid. Agents are equipped with a linear-strength mechanism, called a \emph{line move}, by which an agent can push a whole line of consecutive agents in one of the four directions in a single time-step. We study the problem of transforming an initial shape $S_I$ into a given target shape $S_F$ via a finite sequence of line moves in a distributed model, where each agent can observe the states of nearby agents in a Moore neighbourhood. Our main contribution is the first distributed connectivity-preserving transformation that exploits line moves within a total of $O(n \log_2 n)$ moves, which is asymptotically equivalent to that of the best-known centralised transformations. The algorithm solves the \emph{line formation problem} that allows agents to form a final straight line $S_L$, starting from any shape $ S_I $, whose \emph{associated graph} contains a Hamiltonian path.

On Efficient Connectivity-Preserving Transformations in a Grid

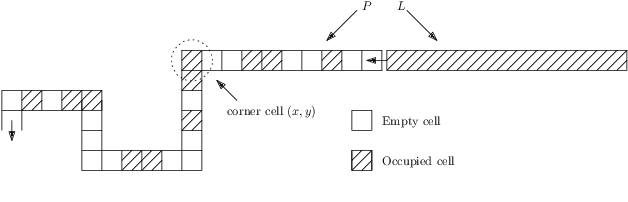
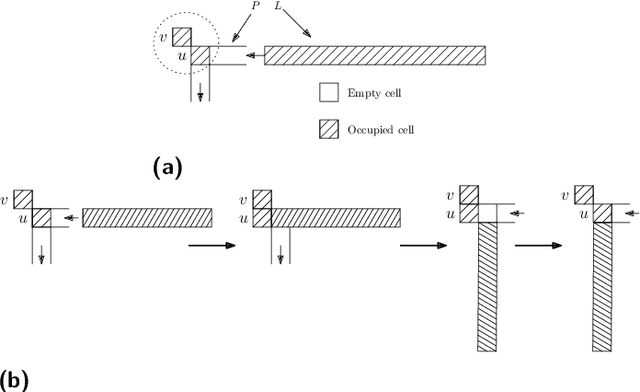
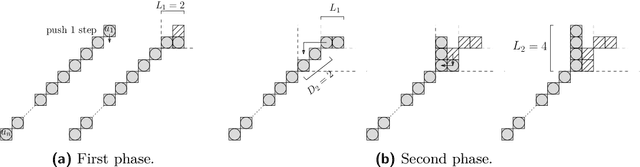
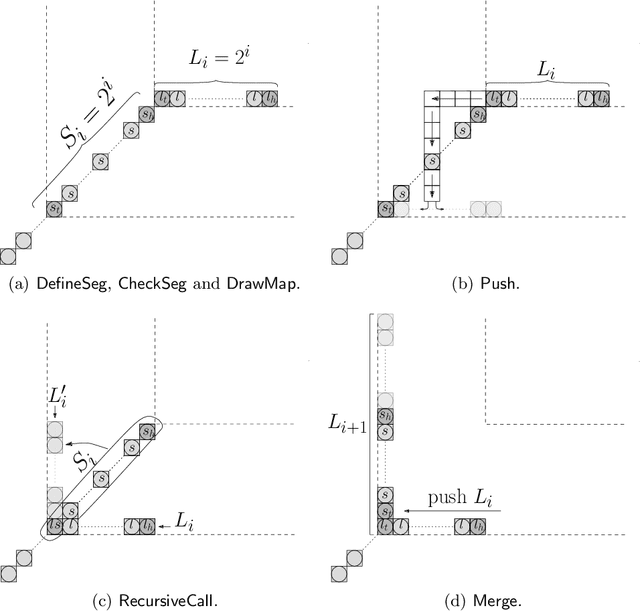
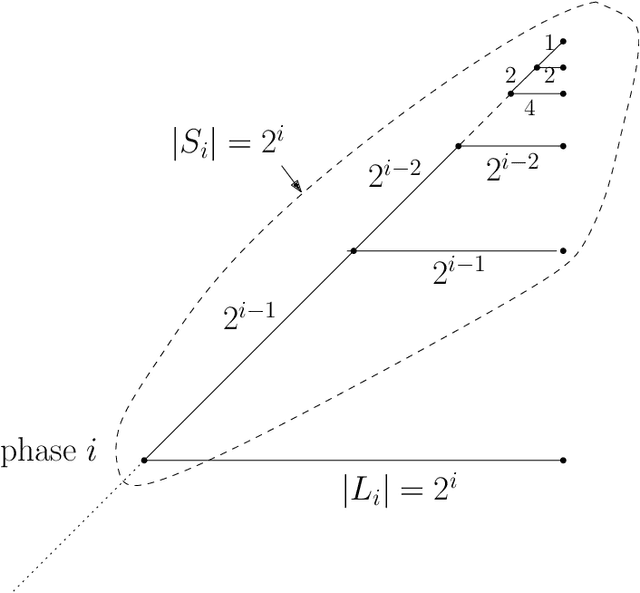
We consider a discrete system of $n$ devices lying on a 2-dimensional square grid and forming an initial connected shape $S_I$. Each device is equipped with a linear-strength mechanism which enables it to move a whole line of consecutive devices in a single time-step. We study the problem of transforming $S_I$ into a given connected target shape $S_F$ of the same number of devices, via a finite sequence of \emph{line moves}. Our focus is on designing \emph{centralised} transformations aiming at \emph{minimising the total number of moves} subject to the constraint of \emph{preserving connectivity} of the shape throughout the course of the transformation. We first give very fast connectivity-preserving transformations for the case in which the \emph{associated graphs} of $ S_I $ and $ S_F $ are isomorphic to a Hamiltonian line. In particular, our transformations make $ O(n \log n $) moves, which is asymptotically equal to the best known running time of connectivity-breaking transformations. Our most general result is then a connectivity-preserving \emph{universal transformation} that can transform any initial connected shape $ S_I $ into any target connected shape $ S_F $, through a sequence of $O(n\sqrt{n})$ moves. Finally, we establish $\Omega(n \log n)$ lower bounds for two restricted sets of transformations. These are the first lower bounds for this model and are matching the best known $ O(n \log n) $ upper bounds.

Optimizing Reachability Sets in Temporal Graphs by Delaying

A temporal graph is a dynamic graph where every edge is assigned a set of integer time labels that indicate at which discrete time step the edge is available. In this paper, we study how changes of the time labels, corresponding to delays on the availability of the edges, affect the reachability sets from given sources. The questions about reachability sets are motivated by numerous applications of temporal graphs in network epidemiology, which aim to minimise the spread of infection, and scheduling problems in supply networks in manufacturing with the opposite objectives of maximising coverage and productivity. We introduce control mechanisms for reachability sets that are based on two natural operations of delaying time events which significantly affecting the chains of these events. The first operation, termed merging, is global and batches together consecutive time labels in the whole network simultaneously. This corresponds to postponing all events until a particular time. The second, imposes independent delays on the time labels of every edge of the graph.cWe provide a thorough investigation of the computational complexity of different objectives related to reachability sets when these operations are used. For the merging operation, i.e. global lockdown effect, we prove NP-hardness results for several minimization and maximization reachability objectives, even for very simple graph structures. For the second operation, independent delays, we prove that the minimization problems are NP-hard when the number of allowed delays is bounded. We complement this with a polynomial-time algorithm for minimising the reachability set in case of unbounded delays.

Pushing Lines Helps: Efficient Universal Centralised Transformations for Programmable Matter

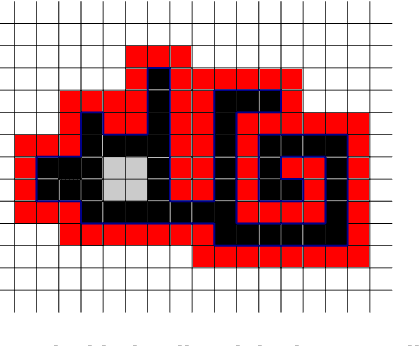
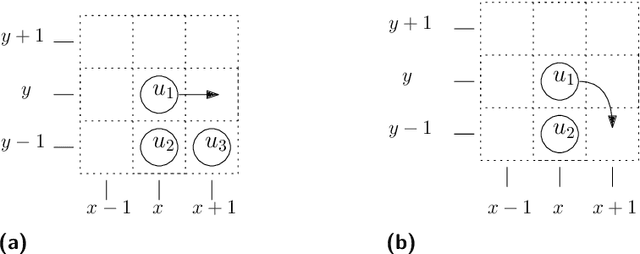
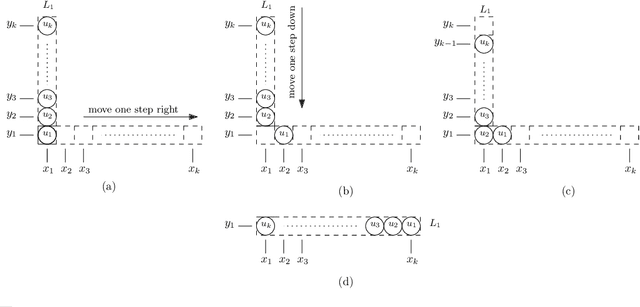
In this paper, we study a discrete system of entities residing on a two-dimensional square grid. Each entity is modelled as a node occupying a distinct cell of the grid. The set of all $n$ nodes forms initially a connected shape $A$. Entities are equipped with a linear-strength pushing mechanism that can push a whole line of entities, from 1 to $n$, in parallel in a single time-step. A target connected shape $B$ is also provided and the goal is to \emph{transform} $A$ into $B$ via a sequence of line movements. Existing models based on local movement of individual nodes, such as rotating or sliding a single node, can be shown to be special cases of the present model, therefore their (inefficient, $\Theta(n^2)$) \emph{universal transformations} carry over. Our main goal is to investigate whether the parallelism inherent in this new type of movement can be exploited for efficient, i.e., sub-quadratic worst-case, transformations. As a first step towards this, we restrict attention solely to centralised transformations and leave the distributed case as a direction for future research. Our results are positive. By focusing on the apparently hard instance of transforming a diagonal $A$ into a straight line $B$, we first obtain transformations of time $O(n\sqrt{n})$ without and with preserving the connectivity of the shape throughout the transformation. Then, we further improve by providing two $O(n\log n)$-time transformations for this problem. By building upon these ideas, we first manage to develop an $O(n\sqrt{n})$-time universal transformation. Our main result is then an $ O(n \log n) $-time universal transformation. We leave as an interesting open problem a suspected $\Omega(n\log n)$-time lower bound.

Temporal logic with predicate abstraction

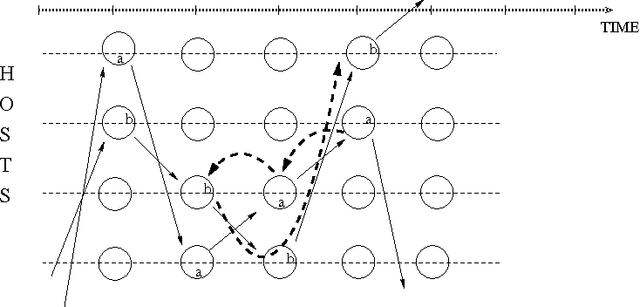
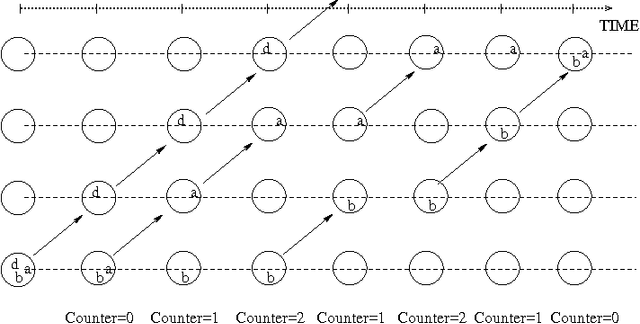
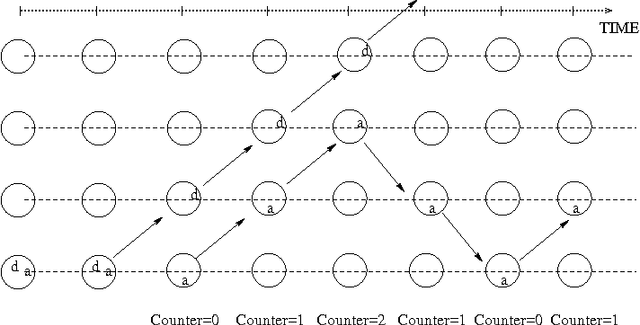
A predicate linear temporal logic LTL_{\lambda,=} without quantifiers but with predicate abstraction mechanism and equality is considered. The models of LTL_{\lambda,=} can be naturally seen as the systems of pebbles (flexible constants) moving over the elements of some (possibly infinite) domain. This allows to use LTL_{\lambda,=} for the specification of dynamic systems using some resources, such as processes using memory locations, mobile agents occupying some sites, etc. On the other hand we show that LTL_{\lambda,=} is not recursively axiomatizable and, therefore, fully automated verification of LTL_{\lambda,=} specifications is not, in general, possible.