Pushing Lines Helps: Efficient Universal Centralised Transformations for Programmable Matter
Paper and Code
Apr 29, 2019
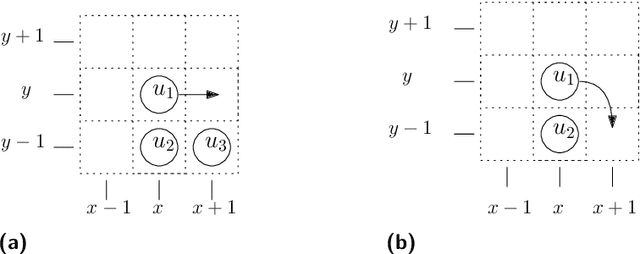
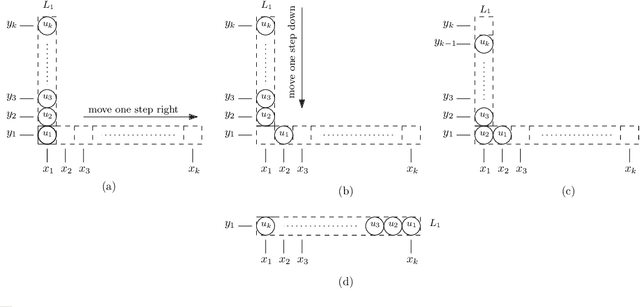
In this paper, we study a discrete system of entities residing on a two-dimensional square grid. Each entity is modelled as a node occupying a distinct cell of the grid. The set of all $n$ nodes forms initially a connected shape $A$. Entities are equipped with a linear-strength pushing mechanism that can push a whole line of entities, from 1 to $n$, in parallel in a single time-step. A target connected shape $B$ is also provided and the goal is to \emph{transform} $A$ into $B$ via a sequence of line movements. Existing models based on local movement of individual nodes, such as rotating or sliding a single node, can be shown to be special cases of the present model, therefore their (inefficient, $\Theta(n^2)$) \emph{universal transformations} carry over. Our main goal is to investigate whether the parallelism inherent in this new type of movement can be exploited for efficient, i.e., sub-quadratic worst-case, transformations. As a first step towards this, we restrict attention solely to centralised transformations and leave the distributed case as a direction for future research. Our results are positive. By focusing on the apparently hard instance of transforming a diagonal $A$ into a straight line $B$, we first obtain transformations of time $O(n\sqrt{n})$ without and with preserving the connectivity of the shape throughout the transformation. Then, we further improve by providing two $O(n\log n)$-time transformations for this problem. By building upon these ideas, we first manage to develop an $O(n\sqrt{n})$-time universal transformation. Our main result is then an $ O(n \log n) $-time universal transformation. We leave as an interesting open problem a suspected $\Omega(n\log n)$-time lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge