Growing Fast without Colliding: Polylogarithmic Time Step Construction of Geometric Shapes

Building on two recent models of [Almalki and Michail, 2022] and [Gupta et al., 2023], we explore the constructive power of a set of geometric growth processes. The studied processes, by applying a sequence of centralized, parallel, and linear-strength growth operations, can construct shapes from smaller shapes or from a singleton exponentially fast. A technical challenge in growing shapes that fast is the need to avoid collisions caused, for example, when the shape breaks, stretches, or self-intersects. We distinguish two types of growth operations -- one that avoids collisions by preserving cycles and one that achieves the same by breaking them -- and two types of graph models. We study the following types of shape reachability questions in these models. Given a class of initial shapes $\mathcal{I}$ and a class of final shapes $\mathcal{F}$, our objective is to determine whether any (some) shape $S \in \mathcal{F}$ can be reached from any shape $S_0 \in \mathcal{I}$ in a number of time steps which is (poly)logarithmic in the size of $S$. For the reachable classes, we additionally present the respective growth processes. In cycle-preserving growth, we study these problems in basic classes of shapes such as paths, spirals, and trees and reveal the importance of the number of turning points as a parameter. We give both positive and negative results. For cycle-breaking growth, we obtain a strong positive result -- a general growth process that can grow any connected shape from a singleton fast.

Collision Detection for Modular Robots -- it is easy to cause collisions and hard to avoid them

We consider geometric collision-detection problems for modular reconfigurable robots. Assuming the nodes (modules) are connected squares on a grid, we investigate the complexity of deciding whether collisions may occur, or can be avoided, if a set of expansion and contraction operations is executed. We study both discrete- and continuous-time models, and allow operations to be coupled into a single parallel group. Our algorithms to decide if a collision may occur run in $O(n^2\log^2 n)$ time, $O(n^2)$ time, or $O(n\log^2 n)$ time, depending on the presence and type of coupled operations, in a continuous-time model for a modular robot with $n$ nodes. To decide if collisions can be avoided, we show that a very restricted version is already NP-complete in the discrete-time model, while the same problem is polynomial in the continuous-time model. A less restricted version is NP-hard in the continuous-time model.

On Geometric Shape Construction via Growth Operations

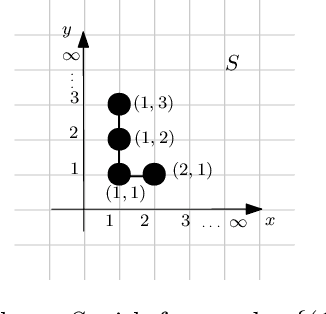
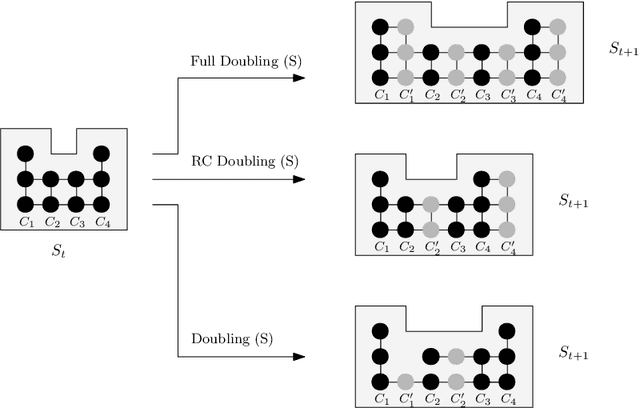
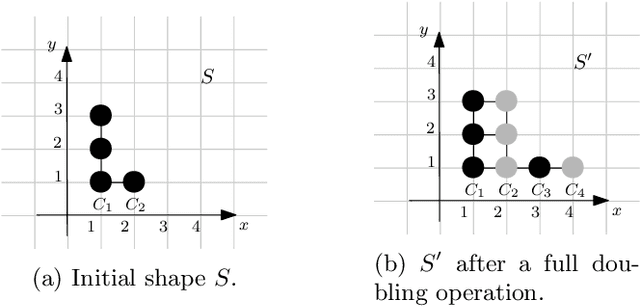
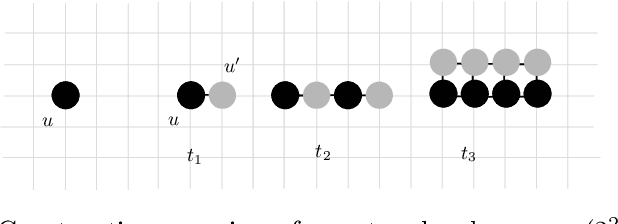
In this work, we investigate novel algorithmic growth processes. In particular, we propose three growth operations, full doubling, RC doubling and doubling, and explore the algorithmic and structural properties of their resulting processes under a geometric setting. In terms of modeling, our system runs on a 2-dimensional grid and operates in discrete time-steps. The process begins with an initial shape $S_I=S_0$ and, in every time-step $t \geq 1$, by applying (in parallel) one or more growth operations of a specific type to the current shape-instance $S_{t-1}$, generates the next instance $S_t$, always satisfying $|S_t| > |S_{t-1}|$. Our goal is to characterize the classes of shapes that can be constructed in $O(\log n)$ or polylog $n$ time-steps and determine whether a final shape $S_F$ can be constructed from an initial shape $S_I$ using a finite sequence of growth operations of a given type, called a constructor of $S_F$. For full doubling, in which, in every time-step, every node generates a new node in a given direction, we completely characterize the structure of the class of shapes that can be constructed from a given initial shape. For RC doubling, in which complete columns or rows double, our main contribution is a linear-time centralized algorithm that for any pair of shapes $S_I$, $S_F$ decides if $S_F$ can be constructed from $S_I$ and, if the answer is yes, returns an $O(\log n)$-time-step constructor of $S_F$ from $S_I$. For the most general doubling operation, where up to individual nodes can double, we show that some shapes cannot be constructed in sub-linear time-steps and give two universal constructors of any $S_F$ from a singleton $S_I$, which are efficient (i.e., up to polylogarithmic time-steps) for large classes of shapes. Both constructors can be computed by polynomial-time centralized algorithms for any shape $S_F$.

Centralised Connectivity-Preserving Transformations by Rotation: 3 Musketeers for all Orthogonal Convex Shapes

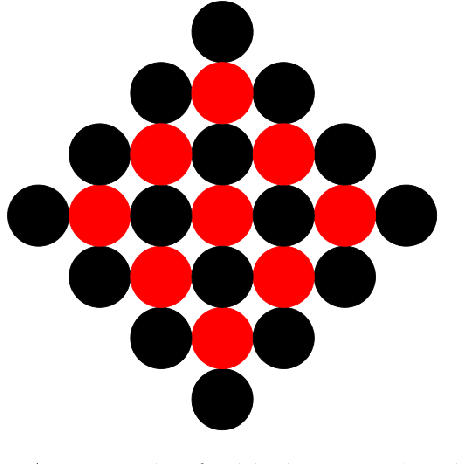
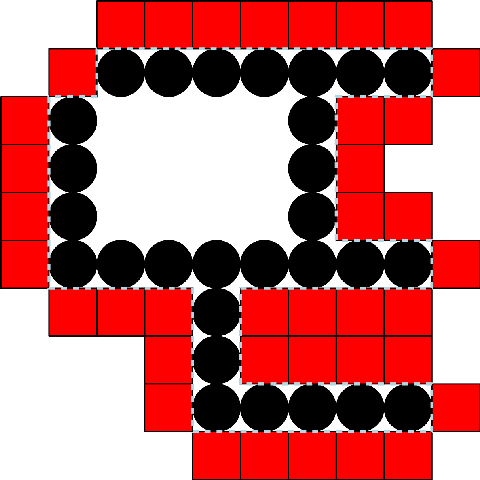
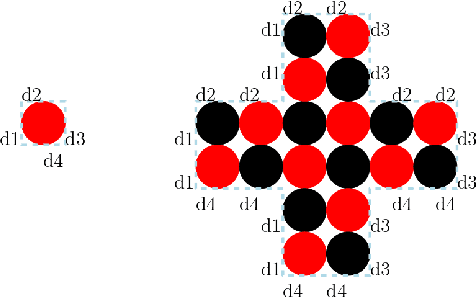
We study a model of programmable matter systems consisting of $n$ devices lying on a 2-dimensional square grid, which are able to perform the minimal mechanical operation of rotating around each other. The goal is to transform an initial shape A into a target shape B. We are interested in characterising the class of shapes which can be transformed into each other in such a scenario, under the additional constraint of maintaining global connectivity at all times. This was one of the main problems left open by $[$Michail et al., JCSS'19$]$. Note that the considered question is about structural feasibility of transformations, which we exclusively deal with via centralised constructive proofs. Distributed solutions are left for future work and form an interesting research direction. Past work made some progress for the special class of nice shapes. We here consider the class of orthogonal convex shapes, where for any two nodes $u, v$ in a horizontal or vertical line on the grid, there is no empty cell between $u$ and $v$. We develop a generic centralised transformation and prove that, for any pair $A$, $B$ of colour-consistent orthogonal convex shapes, it can transform $A$ into $B$. In light of the existence of blocked shapes in the considered class, we use a minimal 3-node seed to trigger the transformation. The running time of our transformation is an optimal $O(n^2)$ sequential moves, where $n=|A|=|B|$. We leave as an open problem the existence of a universal connectivity-preserving transformation with a small seed. Our belief is that the techniques developed in this paper might prove useful to answer this.

Distributed Transformations of Hamiltonian Shapes based on Line Moves

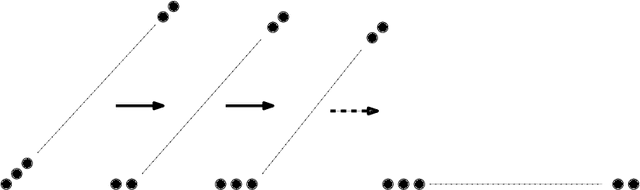
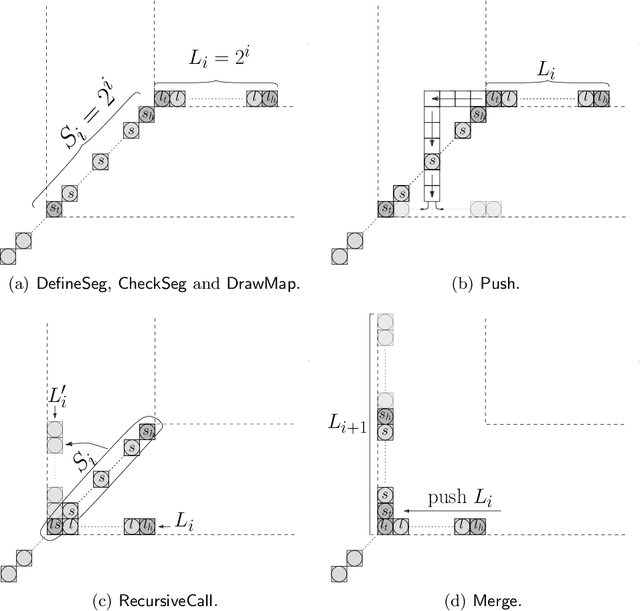
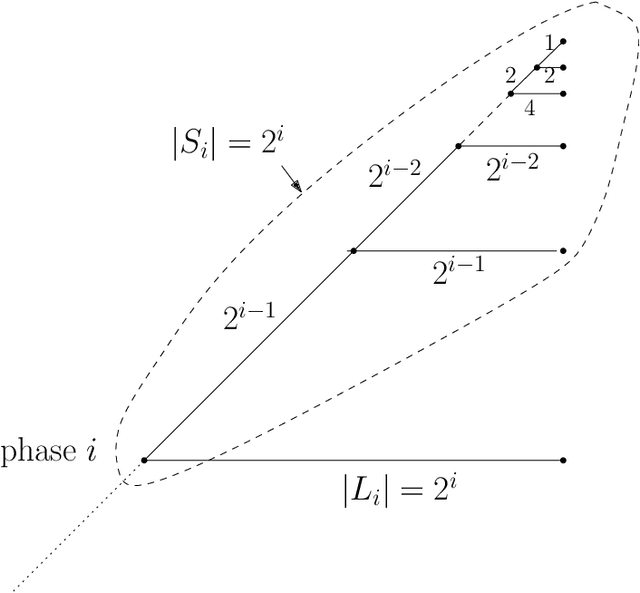
We consider a discrete system of $n$ simple indistinguishable devices, called \emph{agents}, forming a \emph{connected} shape $S_I$ on a two-dimensional square grid. Agents are equipped with a linear-strength mechanism, called a \emph{line move}, by which an agent can push a whole line of consecutive agents in one of the four directions in a single time-step. We study the problem of transforming an initial shape $S_I$ into a given target shape $S_F$ via a finite sequence of line moves in a distributed model, where each agent can observe the states of nearby agents in a Moore neighbourhood. Our main contribution is the first distributed connectivity-preserving transformation that exploits line moves within a total of $O(n \log_2 n)$ moves, which is asymptotically equivalent to that of the best-known centralised transformations. The algorithm solves the \emph{line formation problem} that allows agents to form a final straight line $S_L$, starting from any shape $ S_I $, whose \emph{associated graph} contains a Hamiltonian path.

On Efficient Connectivity-Preserving Transformations in a Grid

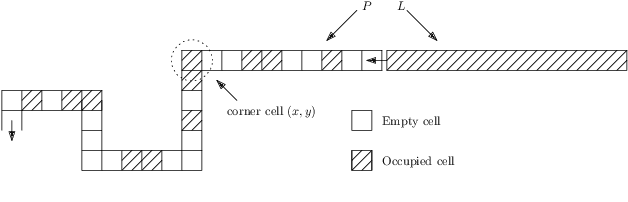
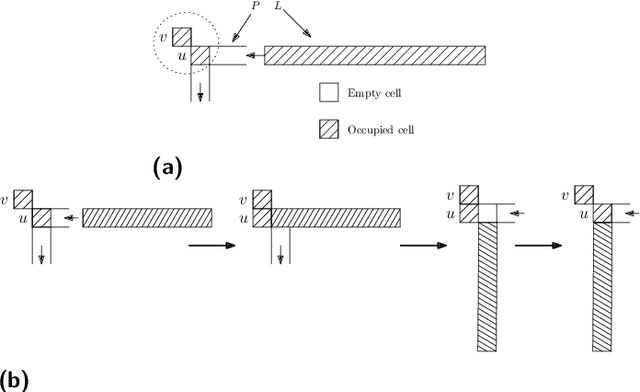
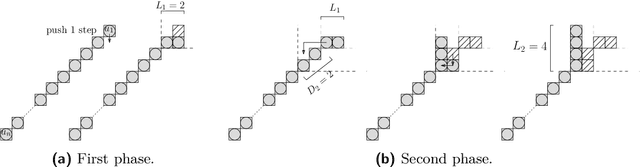
We consider a discrete system of $n$ devices lying on a 2-dimensional square grid and forming an initial connected shape $S_I$. Each device is equipped with a linear-strength mechanism which enables it to move a whole line of consecutive devices in a single time-step. We study the problem of transforming $S_I$ into a given connected target shape $S_F$ of the same number of devices, via a finite sequence of \emph{line moves}. Our focus is on designing \emph{centralised} transformations aiming at \emph{minimising the total number of moves} subject to the constraint of \emph{preserving connectivity} of the shape throughout the course of the transformation. We first give very fast connectivity-preserving transformations for the case in which the \emph{associated graphs} of $ S_I $ and $ S_F $ are isomorphic to a Hamiltonian line. In particular, our transformations make $ O(n \log n $) moves, which is asymptotically equal to the best known running time of connectivity-breaking transformations. Our most general result is then a connectivity-preserving \emph{universal transformation} that can transform any initial connected shape $ S_I $ into any target connected shape $ S_F $, through a sequence of $O(n\sqrt{n})$ moves. Finally, we establish $\Omega(n \log n)$ lower bounds for two restricted sets of transformations. These are the first lower bounds for this model and are matching the best known $ O(n \log n) $ upper bounds.

Pushing Lines Helps: Efficient Universal Centralised Transformations for Programmable Matter

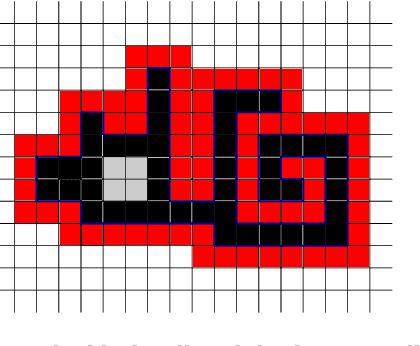
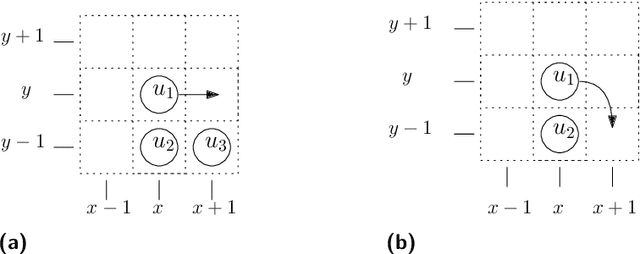
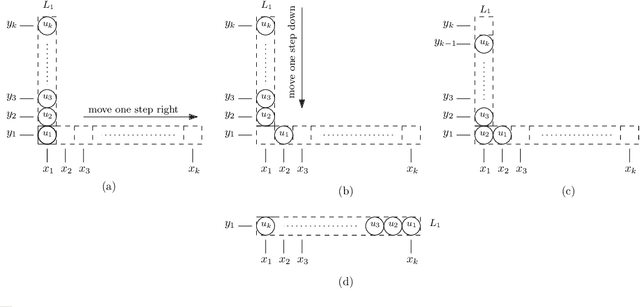
In this paper, we study a discrete system of entities residing on a two-dimensional square grid. Each entity is modelled as a node occupying a distinct cell of the grid. The set of all $n$ nodes forms initially a connected shape $A$. Entities are equipped with a linear-strength pushing mechanism that can push a whole line of entities, from 1 to $n$, in parallel in a single time-step. A target connected shape $B$ is also provided and the goal is to \emph{transform} $A$ into $B$ via a sequence of line movements. Existing models based on local movement of individual nodes, such as rotating or sliding a single node, can be shown to be special cases of the present model, therefore their (inefficient, $\Theta(n^2)$) \emph{universal transformations} carry over. Our main goal is to investigate whether the parallelism inherent in this new type of movement can be exploited for efficient, i.e., sub-quadratic worst-case, transformations. As a first step towards this, we restrict attention solely to centralised transformations and leave the distributed case as a direction for future research. Our results are positive. By focusing on the apparently hard instance of transforming a diagonal $A$ into a straight line $B$, we first obtain transformations of time $O(n\sqrt{n})$ without and with preserving the connectivity of the shape throughout the transformation. Then, we further improve by providing two $O(n\log n)$-time transformations for this problem. By building upon these ideas, we first manage to develop an $O(n\sqrt{n})$-time universal transformation. Our main result is then an $ O(n \log n) $-time universal transformation. We leave as an interesting open problem a suspected $\Omega(n\log n)$-time lower bound.

On the Transformation Capability of Feasible Mechanisms for Programmable Matter

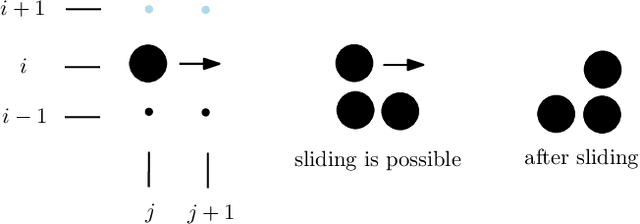
In this work, we study theoretical models of \emph{programmable matter} systems. The systems under consideration consist of spherical modules, kept together by magnetic forces and able to perform two minimal mechanical operations (or movements): \emph{rotate} around a neighbor and \emph{slide} over a line. In terms of modeling, there are $n$ nodes arranged in a 2-dimensional grid and forming some initial \emph{shape}. The goal is for the initial shape $A$ to \emph{transform} to some target shape $B$ by a sequence of movements. Most of the paper focuses on \emph{transformability} questions, meaning whether it is in principle feasible to transform a given shape to another. We first consider the case in which only rotation is available to the nodes. Our main result is that deciding whether two given shapes $A$ and $B$ can be transformed to each other, is in $\mathbf{P}$. We then insist on rotation only and impose the restriction that the nodes must maintain global connectivity throughout the transformation. We prove that the corresponding transformability question is in $\mathbf{PSPACE}$ and study the problem of determining the minimum \emph{seeds} that can make feasible, otherwise infeasible transformations. Next we allow both rotations and slidings and prove universality: any two connected shapes $A,B$ of the same order, can be transformed to each other without breaking connectivity. The worst-case number of movements of the generic strategy is $\Omega(n^2)$. We improve this to $O(n)$ parallel time, by a pipelining strategy, and prove optimality of both by matching lower bounds. In the last part of the paper, we turn our attention to distributed transformations. The nodes are now distributed processes able to perform communicate-compute-move rounds. We provide distributed algorithms for a general type of transformations.