On Efficient Connectivity-Preserving Transformations in a Grid
Paper and Code
May 17, 2020
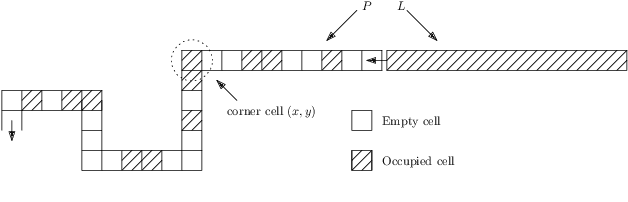
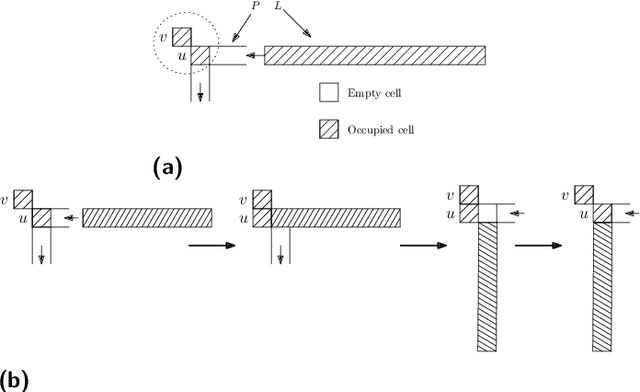
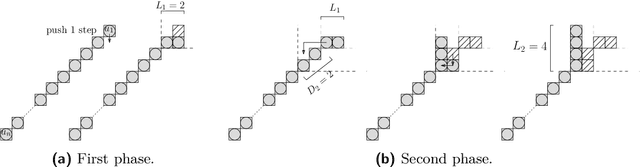
We consider a discrete system of $n$ devices lying on a 2-dimensional square grid and forming an initial connected shape $S_I$. Each device is equipped with a linear-strength mechanism which enables it to move a whole line of consecutive devices in a single time-step. We study the problem of transforming $S_I$ into a given connected target shape $S_F$ of the same number of devices, via a finite sequence of \emph{line moves}. Our focus is on designing \emph{centralised} transformations aiming at \emph{minimising the total number of moves} subject to the constraint of \emph{preserving connectivity} of the shape throughout the course of the transformation. We first give very fast connectivity-preserving transformations for the case in which the \emph{associated graphs} of $ S_I $ and $ S_F $ are isomorphic to a Hamiltonian line. In particular, our transformations make $ O(n \log n $) moves, which is asymptotically equal to the best known running time of connectivity-breaking transformations. Our most general result is then a connectivity-preserving \emph{universal transformation} that can transform any initial connected shape $ S_I $ into any target connected shape $ S_F $, through a sequence of $O(n\sqrt{n})$ moves. Finally, we establish $\Omega(n \log n)$ lower bounds for two restricted sets of transformations. These are the first lower bounds for this model and are matching the best known $ O(n \log n) $ upper bounds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge