Distributed Transformations of Hamiltonian Shapes based on Line Moves

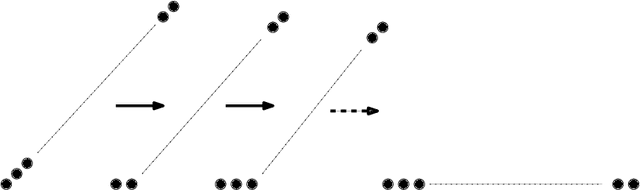
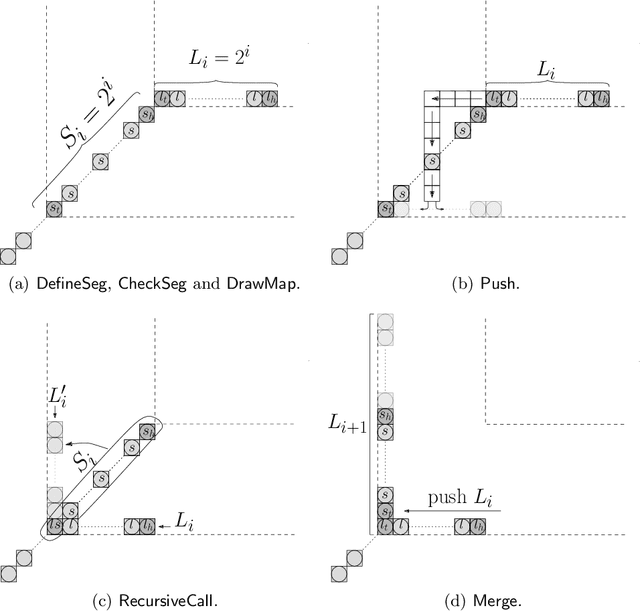
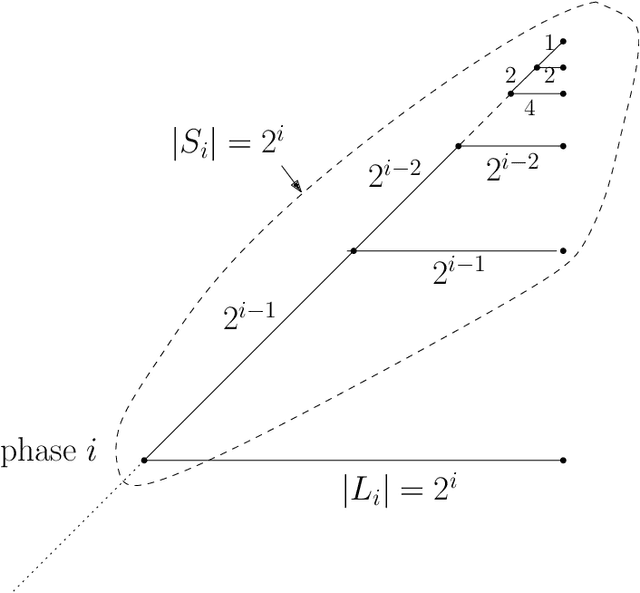
We consider a discrete system of $n$ simple indistinguishable devices, called \emph{agents}, forming a \emph{connected} shape $S_I$ on a two-dimensional square grid. Agents are equipped with a linear-strength mechanism, called a \emph{line move}, by which an agent can push a whole line of consecutive agents in one of the four directions in a single time-step. We study the problem of transforming an initial shape $S_I$ into a given target shape $S_F$ via a finite sequence of line moves in a distributed model, where each agent can observe the states of nearby agents in a Moore neighbourhood. Our main contribution is the first distributed connectivity-preserving transformation that exploits line moves within a total of $O(n \log_2 n)$ moves, which is asymptotically equivalent to that of the best-known centralised transformations. The algorithm solves the \emph{line formation problem} that allows agents to form a final straight line $S_L$, starting from any shape $ S_I $, whose \emph{associated graph} contains a Hamiltonian path.

On Efficient Connectivity-Preserving Transformations in a Grid

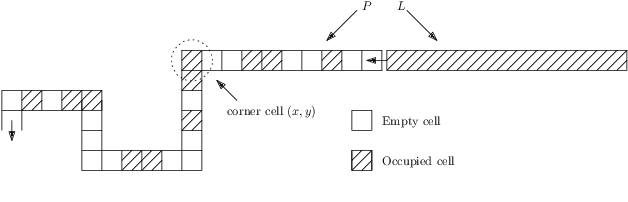
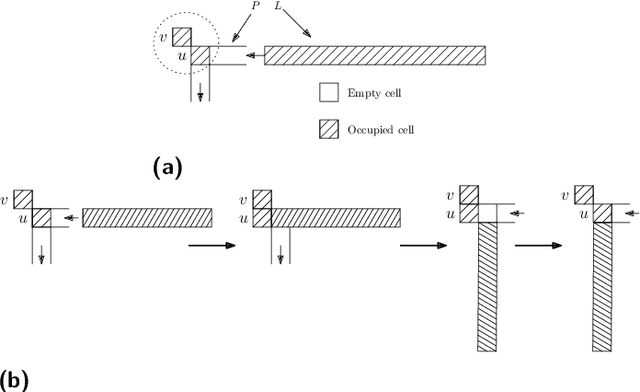
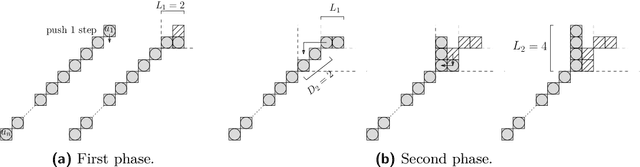
We consider a discrete system of $n$ devices lying on a 2-dimensional square grid and forming an initial connected shape $S_I$. Each device is equipped with a linear-strength mechanism which enables it to move a whole line of consecutive devices in a single time-step. We study the problem of transforming $S_I$ into a given connected target shape $S_F$ of the same number of devices, via a finite sequence of \emph{line moves}. Our focus is on designing \emph{centralised} transformations aiming at \emph{minimising the total number of moves} subject to the constraint of \emph{preserving connectivity} of the shape throughout the course of the transformation. We first give very fast connectivity-preserving transformations for the case in which the \emph{associated graphs} of $ S_I $ and $ S_F $ are isomorphic to a Hamiltonian line. In particular, our transformations make $ O(n \log n $) moves, which is asymptotically equal to the best known running time of connectivity-breaking transformations. Our most general result is then a connectivity-preserving \emph{universal transformation} that can transform any initial connected shape $ S_I $ into any target connected shape $ S_F $, through a sequence of $O(n\sqrt{n})$ moves. Finally, we establish $\Omega(n \log n)$ lower bounds for two restricted sets of transformations. These are the first lower bounds for this model and are matching the best known $ O(n \log n) $ upper bounds.

Pushing Lines Helps: Efficient Universal Centralised Transformations for Programmable Matter

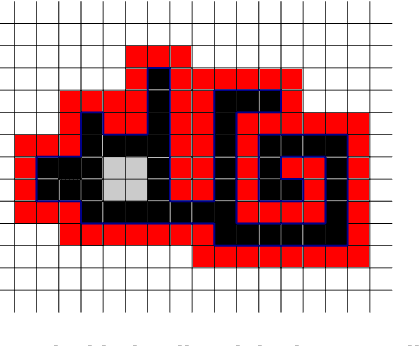
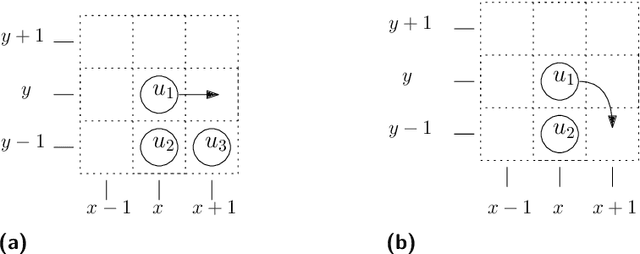
In this paper, we study a discrete system of entities residing on a two-dimensional square grid. Each entity is modelled as a node occupying a distinct cell of the grid. The set of all $n$ nodes forms initially a connected shape $A$. Entities are equipped with a linear-strength pushing mechanism that can push a whole line of entities, from 1 to $n$, in parallel in a single time-step. A target connected shape $B$ is also provided and the goal is to \emph{transform} $A$ into $B$ via a sequence of line movements. Existing models based on local movement of individual nodes, such as rotating or sliding a single node, can be shown to be special cases of the present model, therefore their (inefficient, $\Theta(n^2)$) \emph{universal transformations} carry over. Our main goal is to investigate whether the parallelism inherent in this new type of movement can be exploited for efficient, i.e., sub-quadratic worst-case, transformations. As a first step towards this, we restrict attention solely to centralised transformations and leave the distributed case as a direction for future research. Our results are positive. By focusing on the apparently hard instance of transforming a diagonal $A$ into a straight line $B$, we first obtain transformations of time $O(n\sqrt{n})$ without and with preserving the connectivity of the shape throughout the transformation. Then, we further improve by providing two $O(n\log n)$-time transformations for this problem. By building upon these ideas, we first manage to develop an $O(n\sqrt{n})$-time universal transformation. Our main result is then an $ O(n \log n) $-time universal transformation. We leave as an interesting open problem a suspected $\Omega(n\log n)$-time lower bound.