Growing Fast without Colliding: Polylogarithmic Time Step Construction of Geometric Shapes

Building on two recent models of [Almalki and Michail, 2022] and [Gupta et al., 2023], we explore the constructive power of a set of geometric growth processes. The studied processes, by applying a sequence of centralized, parallel, and linear-strength growth operations, can construct shapes from smaller shapes or from a singleton exponentially fast. A technical challenge in growing shapes that fast is the need to avoid collisions caused, for example, when the shape breaks, stretches, or self-intersects. We distinguish two types of growth operations -- one that avoids collisions by preserving cycles and one that achieves the same by breaking them -- and two types of graph models. We study the following types of shape reachability questions in these models. Given a class of initial shapes $\mathcal{I}$ and a class of final shapes $\mathcal{F}$, our objective is to determine whether any (some) shape $S \in \mathcal{F}$ can be reached from any shape $S_0 \in \mathcal{I}$ in a number of time steps which is (poly)logarithmic in the size of $S$. For the reachable classes, we additionally present the respective growth processes. In cycle-preserving growth, we study these problems in basic classes of shapes such as paths, spirals, and trees and reveal the importance of the number of turning points as a parameter. We give both positive and negative results. For cycle-breaking growth, we obtain a strong positive result -- a general growth process that can grow any connected shape from a singleton fast.

On Geometric Shape Construction via Growth Operations

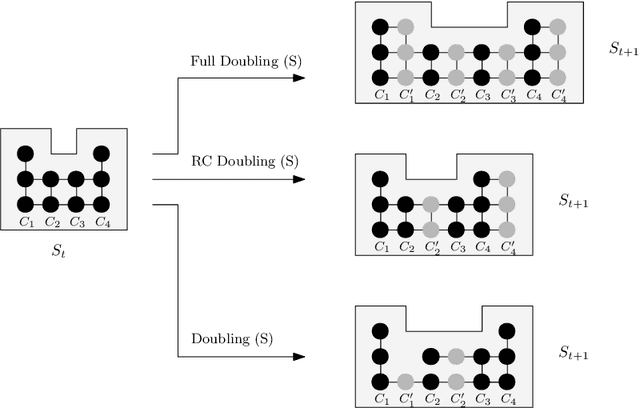
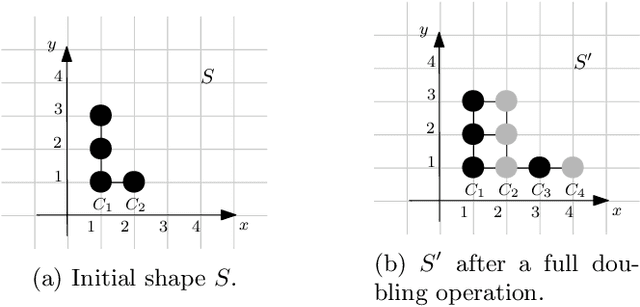
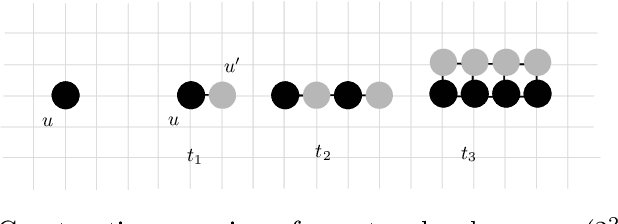
In this work, we investigate novel algorithmic growth processes. In particular, we propose three growth operations, full doubling, RC doubling and doubling, and explore the algorithmic and structural properties of their resulting processes under a geometric setting. In terms of modeling, our system runs on a 2-dimensional grid and operates in discrete time-steps. The process begins with an initial shape $S_I=S_0$ and, in every time-step $t \geq 1$, by applying (in parallel) one or more growth operations of a specific type to the current shape-instance $S_{t-1}$, generates the next instance $S_t$, always satisfying $|S_t| > |S_{t-1}|$. Our goal is to characterize the classes of shapes that can be constructed in $O(\log n)$ or polylog $n$ time-steps and determine whether a final shape $S_F$ can be constructed from an initial shape $S_I$ using a finite sequence of growth operations of a given type, called a constructor of $S_F$. For full doubling, in which, in every time-step, every node generates a new node in a given direction, we completely characterize the structure of the class of shapes that can be constructed from a given initial shape. For RC doubling, in which complete columns or rows double, our main contribution is a linear-time centralized algorithm that for any pair of shapes $S_I$, $S_F$ decides if $S_F$ can be constructed from $S_I$ and, if the answer is yes, returns an $O(\log n)$-time-step constructor of $S_F$ from $S_I$. For the most general doubling operation, where up to individual nodes can double, we show that some shapes cannot be constructed in sub-linear time-steps and give two universal constructors of any $S_F$ from a singleton $S_I$, which are efficient (i.e., up to polylogarithmic time-steps) for large classes of shapes. Both constructors can be computed by polynomial-time centralized algorithms for any shape $S_F$.