Centralised Connectivity-Preserving Transformations by Rotation: 3 Musketeers for all Orthogonal Convex Shapes
Paper and Code
Jul 07, 2022
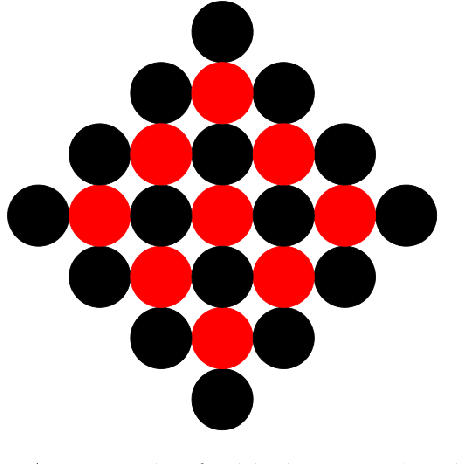
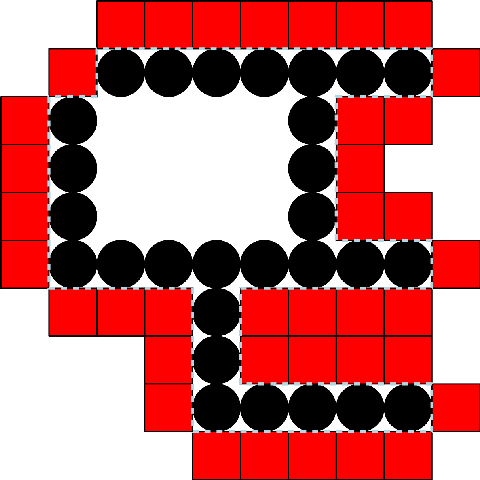
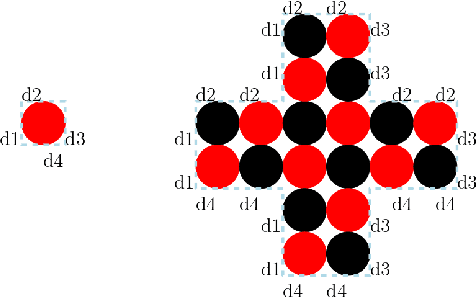
We study a model of programmable matter systems consisting of $n$ devices lying on a 2-dimensional square grid, which are able to perform the minimal mechanical operation of rotating around each other. The goal is to transform an initial shape A into a target shape B. We are interested in characterising the class of shapes which can be transformed into each other in such a scenario, under the additional constraint of maintaining global connectivity at all times. This was one of the main problems left open by $[$Michail et al., JCSS'19$]$. Note that the considered question is about structural feasibility of transformations, which we exclusively deal with via centralised constructive proofs. Distributed solutions are left for future work and form an interesting research direction. Past work made some progress for the special class of nice shapes. We here consider the class of orthogonal convex shapes, where for any two nodes $u, v$ in a horizontal or vertical line on the grid, there is no empty cell between $u$ and $v$. We develop a generic centralised transformation and prove that, for any pair $A$, $B$ of colour-consistent orthogonal convex shapes, it can transform $A$ into $B$. In light of the existence of blocked shapes in the considered class, we use a minimal 3-node seed to trigger the transformation. The running time of our transformation is an optimal $O(n^2)$ sequential moves, where $n=|A|=|B|$. We leave as an open problem the existence of a universal connectivity-preserving transformation with a small seed. Our belief is that the techniques developed in this paper might prove useful to answer this.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge