Argyrios Deligkas
The Complexity of Envy-Free Graph Cutting
Dec 12, 2023Abstract:We consider the problem of fairly dividing a set of heterogeneous divisible resources among agents with different preferences. We focus on the setting where the resources correspond to the edges of a connected graph, every agent must be assigned a connected piece of this graph, and the fairness notion considered is the classical envy freeness. The problem is NP-complete, and we analyze its complexity with respect to two natural complexity measures: the number of agents and the number of edges in the graph. While the problem remains NP-hard even for instances with 2 agents, we provide a dichotomy characterizing the complexity of the problem when the number of agents is constant based on structural properties of the graph. For the latter case, we design a polynomial-time algorithm when the graph has a constant number of edges.
Optimizing Reachability Sets in Temporal Graphs by Delaying
Apr 13, 2020



Abstract:A temporal graph is a dynamic graph where every edge is assigned a set of integer time labels that indicate at which discrete time step the edge is available. In this paper, we study how changes of the time labels, corresponding to delays on the availability of the edges, affect the reachability sets from given sources. The questions about reachability sets are motivated by numerous applications of temporal graphs in network epidemiology, which aim to minimise the spread of infection, and scheduling problems in supply networks in manufacturing with the opposite objectives of maximising coverage and productivity. We introduce control mechanisms for reachability sets that are based on two natural operations of delaying time events which significantly affecting the chains of these events. The first operation, termed merging, is global and batches together consecutive time labels in the whole network simultaneously. This corresponds to postponing all events until a particular time. The second, imposes independent delays on the time labels of every edge of the graph.cWe provide a thorough investigation of the computational complexity of different objectives related to reachability sets when these operations are used. For the merging operation, i.e. global lockdown effect, we prove NP-hardness results for several minimization and maximization reachability objectives, even for very simple graph structures. For the second operation, independent delays, we prove that the minimization problems are NP-hard when the number of allowed delays is bounded. We complement this with a polynomial-time algorithm for minimising the reachability set in case of unbounded delays.
Incentivizing the Dynamic Workforce: Learning Contracts in the Gig-Economy
Nov 16, 2018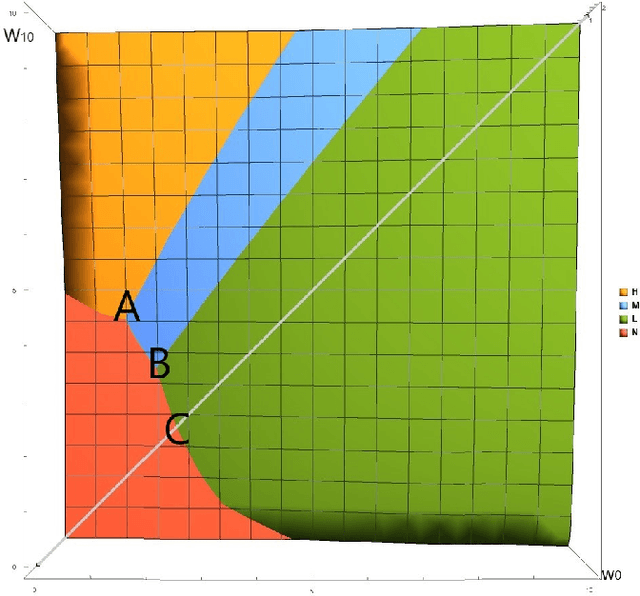
Abstract:In principal-agent models, a principal offers a contract to an agent to perform a certain task. The agent exerts a level of effort that maximizes her utility. The principal is oblivious to the agent's chosen level of effort, and conditions her wage only on possible outcomes. In this work, we consider a model in which the principal is unaware of the agent's utility and action space. She sequentially offers contracts to identical agents, and observes the resulting outcomes. We present an algorithm for learning the optimal contract under mild assumptions. We bound the number of samples needed for the principal obtain a contract that is within $\epsilon$ of her optimal net profit for every $\epsilon>0$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge