The Boundaries of Tractability in Hierarchical Task Network Planning

We study the complexity-theoretic boundaries of tractability for three classical problems in the context of Hierarchical Task Network Planning: the validation of a provided plan, whether an executable plan exists, and whether a given state can be reached by some plan. We show that all three problems can be solved in polynomial time on primitive task networks of constant partial order width (and a generalization thereof), whereas for the latter two problems this holds only under a provably necessary restriction to the state space. Next, we obtain an algorithmic meta-theorem along with corresponding lower bounds to identify tight conditions under which general polynomial-time solvability results can be lifted from primitive to general task networks. Finally, we enrich our investigation by analyzing the parameterized complexity of the three considered problems, and show that (1) fixed-parameter tractability for all three problems can be achieved by replacing the partial order width with the vertex cover number of the network as the parameter, and (2) other classical graph-theoretic parameters of the network (including treewidth, treedepth, and the aforementioned partial order width) do not yield fixed-parameter tractability for any of the three problems.

The Parameterized Complexity of Coordinated Motion Planning

In Coordinated Motion Planning (CMP), we are given a rectangular-grid on which $k$ robots occupy $k$ distinct starting gridpoints and need to reach $k$ distinct destination gridpoints. In each time step, any robot may move to a neighboring gridpoint or stay in its current gridpoint, provided that it does not collide with other robots. The goal is to compute a schedule for moving the $k$ robots to their destinations which minimizes a certain objective target - prominently the number of time steps in the schedule, i.e., the makespan, or the total length traveled by the robots. We refer to the problem arising from minimizing the former objective target as CMP-M and the latter as CMP-L. Both CMP-M and CMP-L are fundamental problems that were posed as the computational geometry challenge of SoCG 2021, and CMP also embodies the famous $(n^2-1)$-puzzle as a special case. In this paper, we settle the parameterized complexity of CMP-M and CMP-L with respect to their two most fundamental parameters: the number of robots, and the objective target. We develop a new approach to establish the fixed-parameter tractability of both problems under the former parameterization that relies on novel structural insights into optimal solutions to the problem. When parameterized by the objective target, we show that CMP-L remains fixed-parameter tractable while CMP-M becomes para-NP-hard. The latter result is noteworthy, not only because it improves the previously-known boundaries of intractability for the problem, but also because the underlying reduction allows us to establish - as a simpler case - the NP-hardness of the classical Vertex Disjoint and Edge Disjoint Paths problems with constant path-lengths on grids.

The Complexity of Optimizing Atomic Congestion

Atomic congestion games are a classic topic in network design, routing, and algorithmic game theory, and are capable of modeling congestion and flow optimization tasks in various application areas. While both the price of anarchy for such games as well as the computational complexity of computing their Nash equilibria are by now well-understood, the computational complexity of computing a system-optimal set of strategies -- that is, a centrally planned routing that minimizes the average cost of agents -- is severely understudied in the literature. We close this gap by identifying the exact boundaries of tractability for the problem through the lens of the parameterized complexity paradigm. After showing that the problem remains highly intractable even on extremely simple networks, we obtain a set of results which demonstrate that the structural parameters which control the computational (in)tractability of the problem are not vertex-separator based in nature (such as, e.g., treewidth), but rather based on edge separators. We conclude by extending our analysis towards the (even more challenging) min-max variant of the problem.

The Complexity of Envy-Free Graph Cutting

We consider the problem of fairly dividing a set of heterogeneous divisible resources among agents with different preferences. We focus on the setting where the resources correspond to the edges of a connected graph, every agent must be assigned a connected piece of this graph, and the fairness notion considered is the classical envy freeness. The problem is NP-complete, and we analyze its complexity with respect to two natural complexity measures: the number of agents and the number of edges in the graph. While the problem remains NP-hard even for instances with 2 agents, we provide a dichotomy characterizing the complexity of the problem when the number of agents is constant based on structural properties of the graph. For the latter case, we design a polynomial-time algorithm when the graph has a constant number of edges.

A Structural Complexity Analysis of Synchronous Dynamical Systems

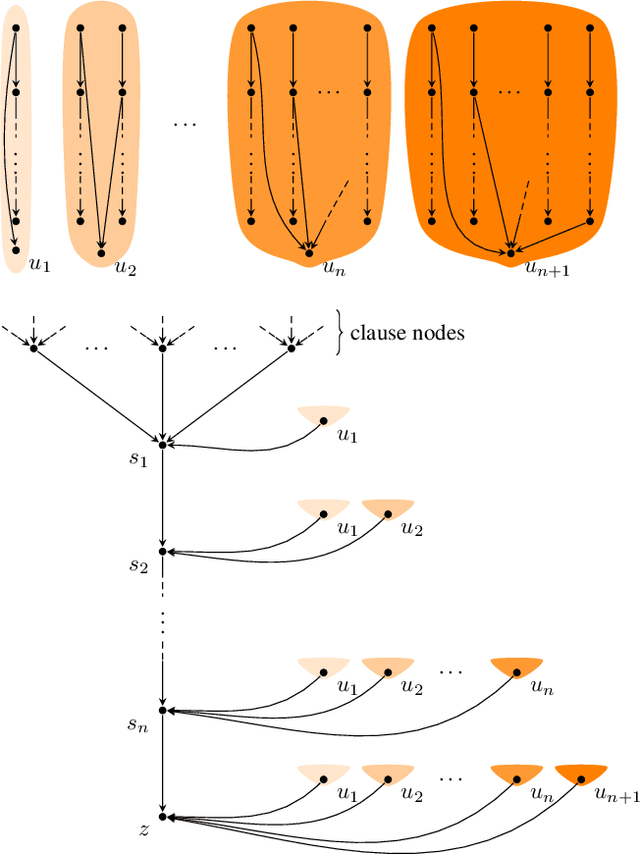
Synchronous dynamic systems are well-established models that have been used to capture a range of phenomena in networks, including opinion diffusion, spread of disease and product adoption. We study the three most notable problems in synchronous dynamic systems: whether the system will transition to a target configuration from a starting configuration, whether the system will reach convergence from a starting configuration, and whether the system is guaranteed to converge from every possible starting configuration. While all three problems were known to be intractable in the classical sense, we initiate the study of their exact boundaries of tractability from the perspective of structural parameters of the network by making use of the more fine-grained parameterized complexity paradigm. As our first result, we consider treewidth - as the most prominent and ubiquitous structural parameter - and show that all three problems remain intractable even on instances of constant treewidth. We complement this negative finding with fixed-parameter algorithms for the former two problems parameterized by treedepth, a well-studied restriction of treewidth. While it is possible to rule out a similar algorithm for convergence guarantee under treedepth, we conclude with a fixed-parameter algorithm for this last problem when parameterized by treedepth and the maximum in-degree.

The Computational Complexity of Concise Hypersphere Classification

Hypersphere classification is a classical and foundational method that can provide easy-to-process explanations for the classification of real-valued and binary data. However, obtaining an (ideally concise) explanation via hypersphere classification is much more difficult when dealing with binary data than real-valued data. In this paper, we perform the first complexity-theoretic study of the hypersphere classification problem for binary data. We use the fine-grained parameterized complexity paradigm to analyze the impact of structural properties that may be present in the input data as well as potential conciseness constraints. Our results include stronger lower bounds and new fixed-parameter algorithms for hypersphere classification of binary data, which can find an exact and concise explanation when one exists.

A Parameterized Theory of PAC Learning

Probably Approximately Correct (i.e., PAC) learning is a core concept of sample complexity theory, and efficient PAC learnability is often seen as a natural counterpart to the class P in classical computational complexity. But while the nascent theory of parameterized complexity has allowed us to push beyond the P-NP ``dichotomy'' in classical computational complexity and identify the exact boundaries of tractability for numerous problems, there is no analogue in the domain of sample complexity that could push beyond efficient PAC learnability. As our core contribution, we fill this gap by developing a theory of parameterized PAC learning which allows us to shed new light on several recent PAC learning results that incorporated elements of parameterized complexity. Within the theory, we identify not one but two notions of fixed-parameter learnability that both form distinct counterparts to the class FPT -- the core concept at the center of the parameterized complexity paradigm -- and develop the machinery required to exclude fixed-parameter learnability. We then showcase the applications of this theory to identify refined boundaries of tractability for CNF and DNF learning as well as for a range of learning problems on graphs.

Threshold Treewidth and Hypertree Width

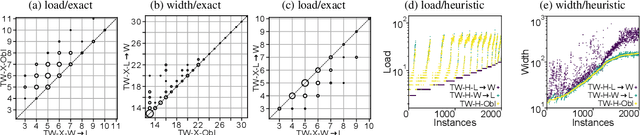
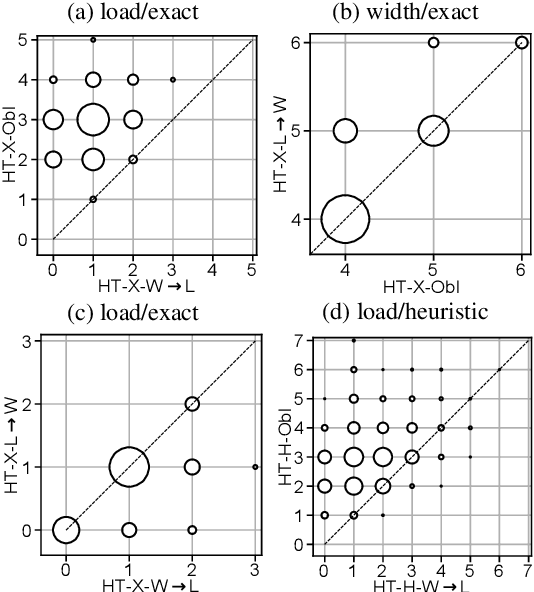
Treewidth and hypertree width have proven to be highly successful structural parameters in the context of the Constraint Satisfaction Problem (CSP). When either of these parameters is bounded by a constant, then CSP becomes solvable in polynomial time. However, here the order of the polynomial in the running time depends on the width, and this is known to be unavoidable; therefore, the problem is not fixed-parameter tractable parameterized by either of these width measures. Here we introduce an enhancement of tree and hypertree width through a novel notion of thresholds, allowing the associated decompositions to take into account information about the computational costs associated with solving the given CSP instance. Aside from introducing these notions, we obtain efficient theoretical as well as empirical algorithms for computing threshold treewidth and hypertree width and show that these parameters give rise to fixed-parameter algorithms for CSP as well as other, more general problems. We complement our theoretical results with experimental evaluations in terms of heuristics as well as exact methods based on SAT/SMT encodings.