Gateways to Tractability for Satisfiability in Pearl's Causal Hierarchy

Pearl's Causal Hierarchy (PCH) is a central framework for reasoning about probabilistic, interventional, and counterfactual statements, yet the satisfiability problem for PCH formulas is computationally intractable in almost all classical settings. We revisit this challenge through the lens of parameterized complexity and identify the first gateways to tractability. Our results include fixed-parameter and XP-algorithms for satisfiability in key probabilistic and counterfactual fragments, using parameters such as primal treewidth and the number of variables, together with matching hardness results that map the limits of tractability. Technically, we depart from the dynamic programming paradigm typically employed for treewidth-based algorithms and instead exploit structural characterizations of well-formed causal models, providing a new algorithmic toolkit for causal reasoning.

Near-Tight Runtime Guarantees for Many-Objective Evolutionary Algorithms

Despite significant progress in the field of mathematical runtime analysis of multi-objective evolutionary algorithms (MOEAs), the performance of MOEAs on discrete many-objective problems is little understood. In particular, the few existing bounds for the SEMO, global SEMO, and SMS-EMOA algorithms on classic benchmarks are all roughly quadratic in the size of the Pareto front. In this work, we prove near-tight runtime guarantees for these three algorithms on the four most common benchmark problems OneMinMax, CountingOnesCountingZeros, LeadingOnesTrailingZeros, and OneJumpZeroJump, and this for arbitrary numbers of objectives. Our bounds depend only linearly on the Pareto front size, showing that these MOEAs on these benchmarks cope much better with many objectives than what previous works suggested. Our bounds are tight apart from small polynomial factors in the number of objectives and length of bitstrings. This is the first time that such tight bounds are proven for many-objective uses of these MOEAs. While it is known that such results cannot hold for the NSGA-II, we do show that our bounds, via a recent structural result, transfer to the NSGA-III algorithm.

The Boundaries of Tractability in Hierarchical Task Network Planning

We study the complexity-theoretic boundaries of tractability for three classical problems in the context of Hierarchical Task Network Planning: the validation of a provided plan, whether an executable plan exists, and whether a given state can be reached by some plan. We show that all three problems can be solved in polynomial time on primitive task networks of constant partial order width (and a generalization thereof), whereas for the latter two problems this holds only under a provably necessary restriction to the state space. Next, we obtain an algorithmic meta-theorem along with corresponding lower bounds to identify tight conditions under which general polynomial-time solvability results can be lifted from primitive to general task networks. Finally, we enrich our investigation by analyzing the parameterized complexity of the three considered problems, and show that (1) fixed-parameter tractability for all three problems can be achieved by replacing the partial order width with the vertex cover number of the network as the parameter, and (2) other classical graph-theoretic parameters of the network (including treewidth, treedepth, and the aforementioned partial order width) do not yield fixed-parameter tractability for any of the three problems.

The First Proven Performance Guarantees for the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) on a Combinatorial Optimization Problem

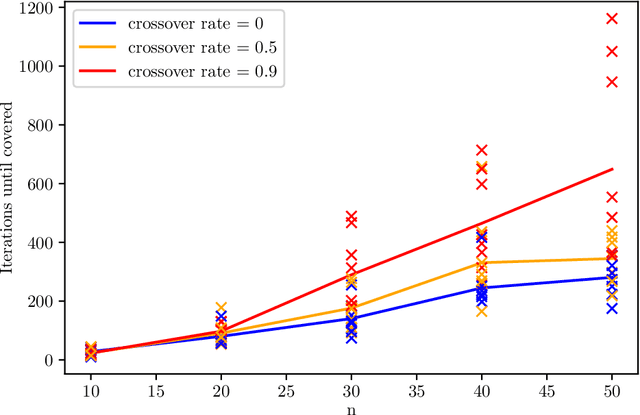
The Non-dominated Sorting Genetic Algorithm-II (NSGA-II) is one of the most prominent algorithms to solve multi-objective optimization problems. Recently, the first mathematical runtime guarantees have been obtained for this algorithm, however only for synthetic benchmark problems. In this work, we give the first proven performance guarantees for a classic optimization problem, the NP-complete bi-objective minimum spanning tree problem. More specifically, we show that the NSGA-II with population size $N \ge 4((n-1) w_{\max} + 1)$ computes all extremal points of the Pareto front in an expected number of $O(m^2 n w_{\max} \log(n w_{\max}))$ iterations, where $n$ is the number of vertices, $m$ the number of edges, and $w_{\max}$ is the maximum edge weight in the problem instance. This result confirms, via mathematical means, the good performance of the NSGA-II observed empirically. It also shows that mathematical analyses of this algorithm are not only possible for synthetic benchmark problems, but also for more complex combinatorial optimization problems. As a side result, we also obtain a new analysis of the performance of the global SEMO algorithm on the bi-objective minimum spanning tree problem, which improves the previous best result by a factor of $|F|$, the number of extremal points of the Pareto front, a set that can be as large as $n w_{\max}$. The main reason for this improvement is our observation that both multi-objective evolutionary algorithms find the different extremal points in parallel rather than sequentially, as assumed in the previous proofs.

Fair Correlation Clustering in Forests

The study of algorithmic fairness received growing attention recently. This stems from the awareness that bias in the input data for machine learning systems may result in discriminatory outputs. For clustering tasks, one of the most central notions of fairness is the formalization by Chierichetti, Kumar, Lattanzi, and Vassilvitskii [NeurIPS 2017]. A clustering is said to be fair, if each cluster has the same distribution of manifestations of a sensitive attribute as the whole input set. This is motivated by various applications where the objects to be clustered have sensitive attributes that should not be over- or underrepresented. We discuss the applicability of this fairness notion to Correlation Clustering. The existing literature on the resulting Fair Correlation Clustering problem either presents approximation algorithms with poor approximation guarantees or severely limits the possible distributions of the sensitive attribute (often only two manifestations with a 1:1 ratio are considered). Our goal is to understand if there is hope for better results in between these two extremes. To this end, we consider restricted graph classes which allow us to characterize the distributions of sensitive attributes for which this form of fairness is tractable from a complexity point of view. While existing work on Fair Correlation Clustering gives approximation algorithms, we focus on exact solutions and investigate whether there are efficiently solvable instances. The unfair version of Correlation Clustering is trivial on forests, but adding fairness creates a surprisingly rich picture of complexities. We give an overview of the distributions and types of forests where Fair Correlation Clustering turns from tractable to intractable. The most surprising insight to us is the fact that the cause of the hardness of Fair Correlation Clustering is not the strictness of the fairness condition.

A Mathematical Runtime Analysis of the Non-dominated Sorting Genetic Algorithm III

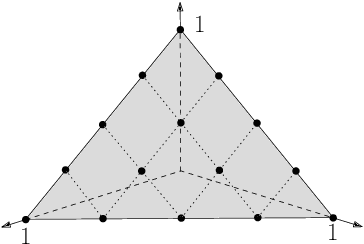
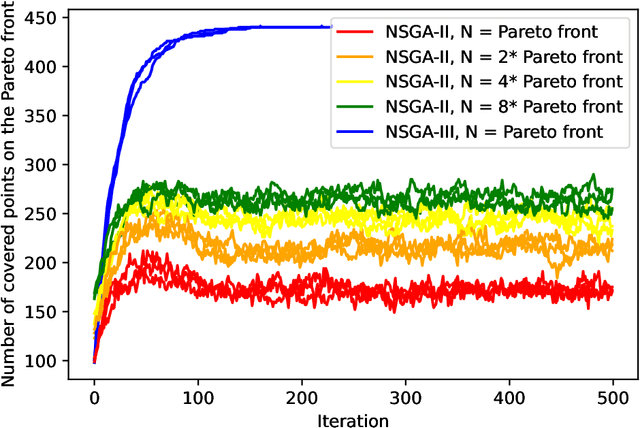
The NSGA-II (Non-dominated Sorting Genetic Algorithm) is the most prominent multi-objective evolutionary algorithm for real-world applications. While it performs evidently well on bi-objective benchmarks, empirical studies suggest that its performance worsens when applied to functions with more than two objectives. As a remedy, the NSGA-III with a slightly adapted selection for the next generation was proposed. In this work, we provide the first mathematical runtime analysis of the NSGA-III, on a 3-objective variant of the \textsc{OneMinMax} benchmark. We prove that employing sufficiently many (at least $\frac{2n^2}{3}+\frac{5n}{\sqrt{3}}+3$) reference points ensures that once a solution for a certain trade-off between the objectives is found, the population contains such a solution in all future iterations. Building on this observation, we show that the expected number of iterations until the population covers the Pareto front is in $O(n^3)$. This result holds for all population sizes that are at least the size of the Pareto front.

Maps for Learning Indexable Classes

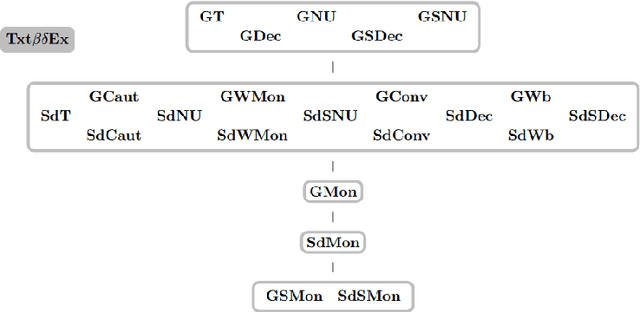
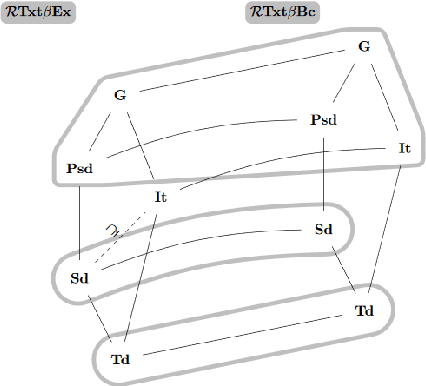
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.