Makespan Minimization in Split Learning: From Theory to Practice

Split learning recently emerged as a solution for distributed machine learning with heterogeneous IoT devices, where clients can offload part of their training to computationally-powerful helpers. The core challenge in split learning is to minimize the training time by jointly devising the client-helper assignment and the schedule of tasks at the helpers. We first study the model where each helper has a memory cardinality constraint on how many clients it may be assigned, which represents the case of homogeneous tasks. Through complexity theory, we rule out exact polynomial-time algorithms and approximation schemes even for highly restricted instances of this problem. We complement these negative results with a non-trivial polynomial-time 5-approximation algorithm. Building on this, we then focus on the more general heterogeneous task setting considered by Tirana et al. [INFOCOM 2024], where helpers have memory capacity constraints and clients have variable memory costs. In this case, we prove that, unless P=NP, the problem cannot admit a polynomial-time approximation algorithm for any approximation factor. However, by adapting our aforementioned 5-approximation algorithm, we develop a novel heuristic for the heterogeneous task setting and show that it outperforms heuristics from prior works through extensive experiments.

Non-Clashing Teaching in Graphs: Algorithms, Complexity, and Bounds

Kirkpatrick et al. [ALT 2019] and Fallat et al. [JMLR 2023] introduced non-clashing teaching and proved that it is the most efficient batch machine teaching model satisfying the collusion-avoidance benchmark established in the seminal work of Goldman and Mathias [COLT 1993]. Recently, (positive) non-clashing teaching was thoroughly studied for balls in graphs, yielding numerous algorithmic and combinatorial results. In particular, Chalopin et al. [COLT 2024] and Ganian et al. [ICLR 2025] gave an almost complete picture of the complexity landscape of the positive variant, showing that it is tractable only for restricted graph classes due to the non-trivial nature of the problem and concept class. In this work, we consider (positive) non-clashing teaching for closed neighborhoods in graphs. This concept class is not only extensively studied in various related contexts, but it also exhibits broad generality, as any finite binary concept class can be equivalently represented by a set of closed neighborhoods in a graph. In comparison to the works on balls in graphs, we provide improved algorithmic results, notably including FPT algorithms for more general classes of parameters, and we complement these results by deriving stronger lower bounds. Lastly, we obtain combinatorial upper bounds for wider classes of graphs.

The Computational Complexity of Positive Non-Clashing Teaching in Graphs

We study the classical and parameterized complexity of computing the positive non-clashing teaching dimension of a set of concepts, that is, the smallest number of examples per concept required to successfully teach an intelligent learner under the considered, previously established model. For any class of concepts, it is known that this problem can be effortlessly transferred to the setting of balls in a graph G. We establish (1) the NP-hardness of the problem even when restricted to instances with positive non-clashing teaching dimension k=2 and where all balls in the graph are present, (2) near-tight running time upper and lower bounds for the problem on general graphs, (3) fixed-parameter tractability when parameterized by the vertex integrity of G, and (4) a lower bound excluding fixed-parameter tractability when parameterized by the feedback vertex number and pathwidth of G, even when combined with k. Our results provide a nearly complete understanding of the complexity landscape of computing the positive non-clashing teaching dimension and answer open questions from the literature.

The Boundaries of Tractability in Hierarchical Task Network Planning

We study the complexity-theoretic boundaries of tractability for three classical problems in the context of Hierarchical Task Network Planning: the validation of a provided plan, whether an executable plan exists, and whether a given state can be reached by some plan. We show that all three problems can be solved in polynomial time on primitive task networks of constant partial order width (and a generalization thereof), whereas for the latter two problems this holds only under a provably necessary restriction to the state space. Next, we obtain an algorithmic meta-theorem along with corresponding lower bounds to identify tight conditions under which general polynomial-time solvability results can be lifted from primitive to general task networks. Finally, we enrich our investigation by analyzing the parameterized complexity of the three considered problems, and show that (1) fixed-parameter tractability for all three problems can be achieved by replacing the partial order width with the vertex cover number of the network as the parameter, and (2) other classical graph-theoretic parameters of the network (including treewidth, treedepth, and the aforementioned partial order width) do not yield fixed-parameter tractability for any of the three problems.

The Complexity of Optimizing Atomic Congestion

Atomic congestion games are a classic topic in network design, routing, and algorithmic game theory, and are capable of modeling congestion and flow optimization tasks in various application areas. While both the price of anarchy for such games as well as the computational complexity of computing their Nash equilibria are by now well-understood, the computational complexity of computing a system-optimal set of strategies -- that is, a centrally planned routing that minimizes the average cost of agents -- is severely understudied in the literature. We close this gap by identifying the exact boundaries of tractability for the problem through the lens of the parameterized complexity paradigm. After showing that the problem remains highly intractable even on extremely simple networks, we obtain a set of results which demonstrate that the structural parameters which control the computational (in)tractability of the problem are not vertex-separator based in nature (such as, e.g., treewidth), but rather based on edge separators. We conclude by extending our analysis towards the (even more challenging) min-max variant of the problem.

Non-Clashing Teaching Maps for Balls in Graphs

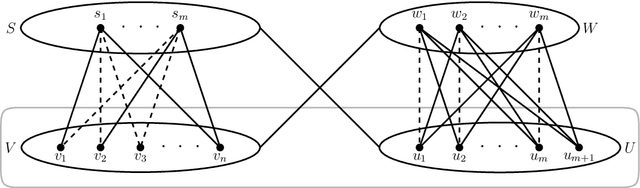
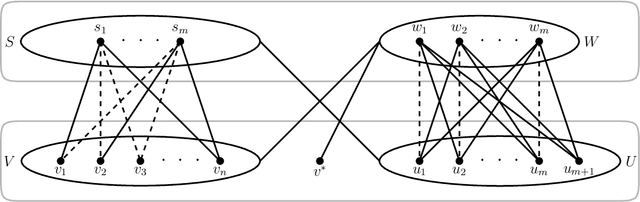
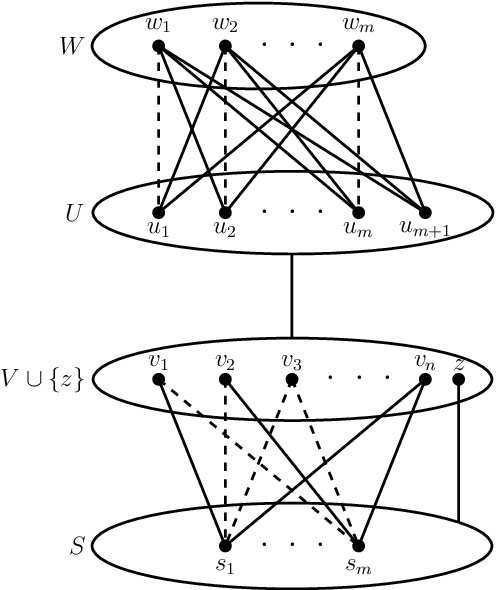
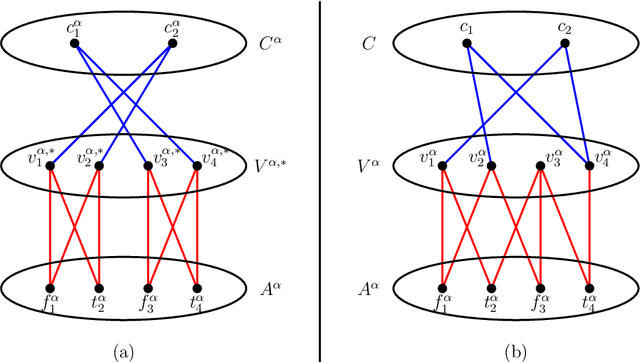
Recently, Kirkpatrick et al. [ALT 2019] and Fallat et al. [JMLR 2023] introduced non-clashing teaching and showed it to be the most efficient machine teaching model satisfying the benchmark for collusion-avoidance set by Goldman and Mathias. A teaching map $T$ for a concept class $\cal{C}$ assigns a (teaching) set $T(C)$ of examples to each concept $C \in \cal{C}$. A teaching map is non-clashing if no pair of concepts are consistent with the union of their teaching sets. The size of a non-clashing teaching map (NCTM) $T$ is the maximum size of a $T(C)$, $C \in \cal{C}$. The non-clashing teaching dimension NCTD$(\cal{C})$ of $\cal{C}$ is the minimum size of an NCTM for $\cal{C}$. NCTM$^+$ and NCTD$^+(\cal{C})$ are defined analogously, except the teacher may only use positive examples. We study NCTMs and NCTM$^+$s for the concept class $\mathcal{B}(G)$ consisting of all balls of a graph $G$. We show that the associated decision problem {\sc B-NCTD$^+$} for NCTD$^+$ is NP-complete in split, co-bipartite, and bipartite graphs. Surprisingly, we even prove that, unless the ETH fails, {\sc B-NCTD$^+$} does not admit an algorithm running in time $2^{2^{o(vc)}}\cdot n^{O(1)}$, nor a kernelization algorithm outputting a kernel with $2^{o(vc)}$ vertices, where vc is the vertex cover number of $G$. These are extremely rare results: it is only the second (fourth, resp.) problem in NP to admit a double-exponential lower bound parameterized by vc (treewidth, resp.), and only one of very few problems to admit an ETH-based conditional lower bound on the number of vertices in a kernel. We complement these lower bounds with matching upper bounds. For trees, interval graphs, cycles, and trees of cycles, we derive NCTM$^+$s or NCTMs for $\mathcal{B}(G)$ of size proportional to its VC-dimension. For Gromov-hyperbolic graphs, we design an approximate NCTM$^+$ for $\mathcal{B}(G)$ of size 2.

Sample compression schemes for balls in graphs

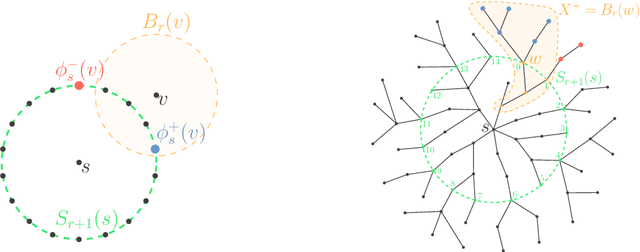
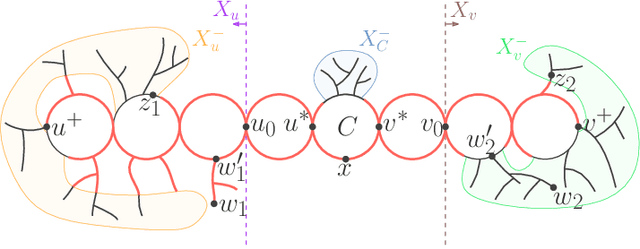
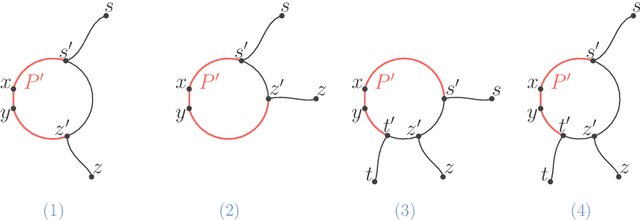
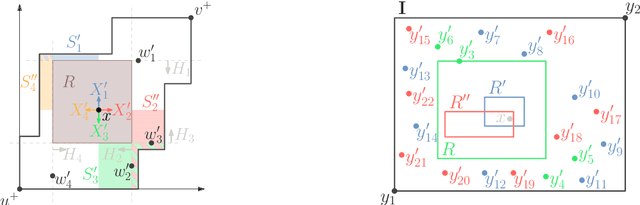
One of the open problems in machine learning is whether any set-family of VC-dimension $d$ admits a sample compression scheme of size~$O(d)$. In this paper, we study this problem for balls in graphs. For balls of arbitrary radius $r$, we design proper sample compression schemes of size $2$ for trees, of size $3$ for cycles, of size $4$ for interval graphs, of size $6$ for trees of cycles, and of size $22$ for cube-free median graphs. For balls of a given radius, we design proper labeled sample compression schemes of size $2$ for trees and of size $4$ for interval graphs. We also design approximate sample compression schemes of size 2 for balls of $\delta$-hyperbolic graphs.