Non-Clashing Teaching Maps for Balls in Graphs

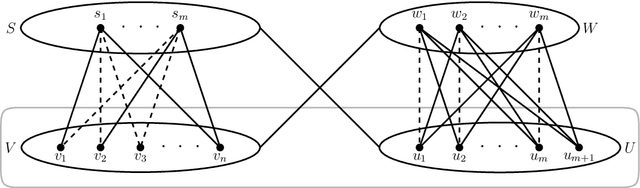
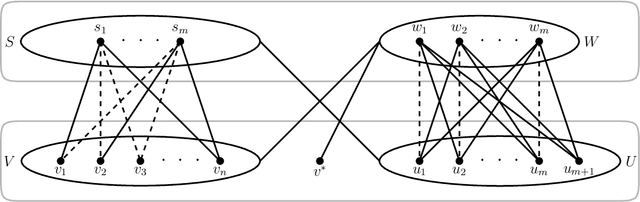
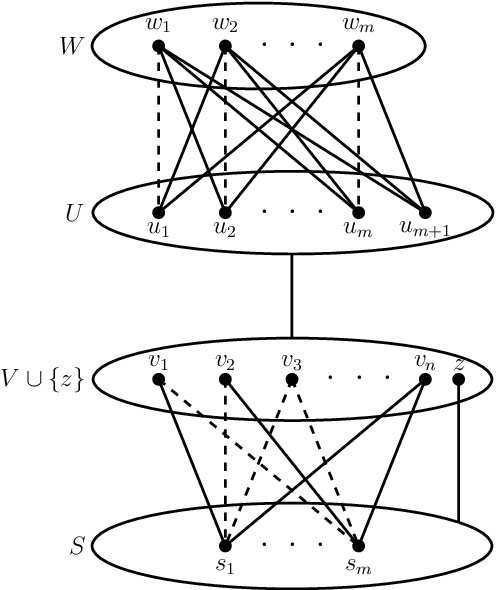
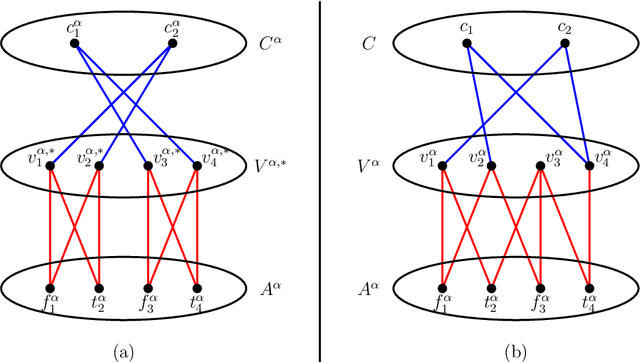
Recently, Kirkpatrick et al. [ALT 2019] and Fallat et al. [JMLR 2023] introduced non-clashing teaching and showed it to be the most efficient machine teaching model satisfying the benchmark for collusion-avoidance set by Goldman and Mathias. A teaching map $T$ for a concept class $\cal{C}$ assigns a (teaching) set $T(C)$ of examples to each concept $C \in \cal{C}$. A teaching map is non-clashing if no pair of concepts are consistent with the union of their teaching sets. The size of a non-clashing teaching map (NCTM) $T$ is the maximum size of a $T(C)$, $C \in \cal{C}$. The non-clashing teaching dimension NCTD$(\cal{C})$ of $\cal{C}$ is the minimum size of an NCTM for $\cal{C}$. NCTM$^+$ and NCTD$^+(\cal{C})$ are defined analogously, except the teacher may only use positive examples. We study NCTMs and NCTM$^+$s for the concept class $\mathcal{B}(G)$ consisting of all balls of a graph $G$. We show that the associated decision problem {\sc B-NCTD$^+$} for NCTD$^+$ is NP-complete in split, co-bipartite, and bipartite graphs. Surprisingly, we even prove that, unless the ETH fails, {\sc B-NCTD$^+$} does not admit an algorithm running in time $2^{2^{o(vc)}}\cdot n^{O(1)}$, nor a kernelization algorithm outputting a kernel with $2^{o(vc)}$ vertices, where vc is the vertex cover number of $G$. These are extremely rare results: it is only the second (fourth, resp.) problem in NP to admit a double-exponential lower bound parameterized by vc (treewidth, resp.), and only one of very few problems to admit an ETH-based conditional lower bound on the number of vertices in a kernel. We complement these lower bounds with matching upper bounds. For trees, interval graphs, cycles, and trees of cycles, we derive NCTM$^+$s or NCTMs for $\mathcal{B}(G)$ of size proportional to its VC-dimension. For Gromov-hyperbolic graphs, we design an approximate NCTM$^+$ for $\mathcal{B}(G)$ of size 2.

Sample compression schemes for balls in graphs

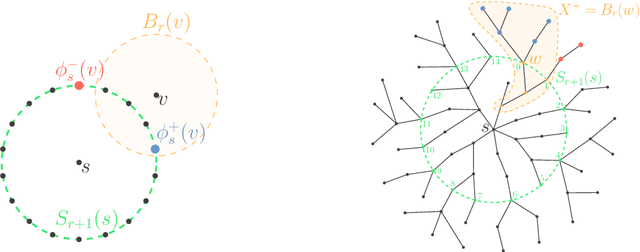
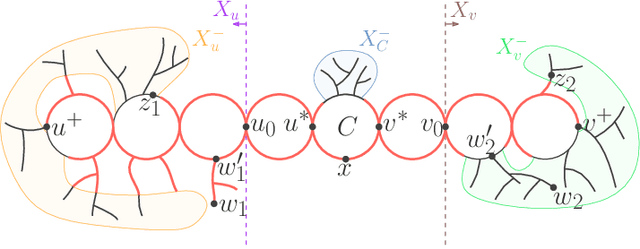
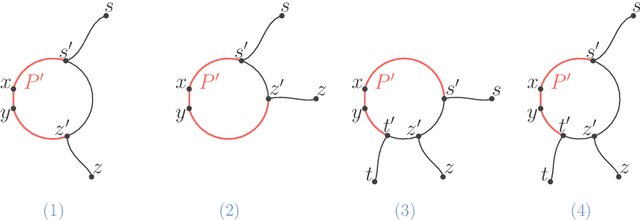
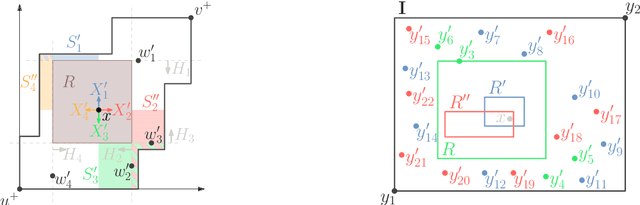
One of the open problems in machine learning is whether any set-family of VC-dimension $d$ admits a sample compression scheme of size~$O(d)$. In this paper, we study this problem for balls in graphs. For balls of arbitrary radius $r$, we design proper sample compression schemes of size $2$ for trees, of size $3$ for cycles, of size $4$ for interval graphs, of size $6$ for trees of cycles, and of size $22$ for cube-free median graphs. For balls of a given radius, we design proper labeled sample compression schemes of size $2$ for trees and of size $4$ for interval graphs. We also design approximate sample compression schemes of size 2 for balls of $\delta$-hyperbolic graphs.

Labeled sample compression schemes for complexes of oriented matroids

We show that the topes of a complex of oriented matroids (abbreviated COM) of VC-dimension $d$ admit a proper labeled sample compression scheme of size $d$. This considerably extends results of Moran and Warmuth and the authors and is a step towards the sample compression conjecture -- one of the oldest open in computational learning theory. On the one hand, our approach exploits the rich combinatorial cell structure of COMs via oriented matroid theory. On the other hand viewing tope graphs of COMs as partial cubes creates a fruitful link to metric graph theory

Unlabeled sample compression schemes and corner peelings for ample and maximum classes

We examine connections between combinatorial notions that arise in machine learning and topological notions in cubical/simplicial geometry. These connections enable to export results from geometry to machine learning. Our first main result is based on a geometric construction by Tracy Hall (2004) of a partial shelling of the cross-polytope which can not be extended. We use it to derive a maximum class of VC dimension 3 that has no corners. This refutes several previous works in machine learning from the past 11 years. In particular, it implies that all previous constructions of optimal unlabeled sample compression schemes for maximum classes are erroneous. On the positive side we present a new construction of an unlabeled sample compression scheme for maximum classes. We leave as open whether our unlabeled sample compression scheme extends to ample (a.k.a. lopsided or extremal) classes, which represent a natural and far-reaching generalization of maximum classes. Towards resolving this question, we provide a geometric characterization in terms of unique sink orientations of the 1-skeletons of associated cubical complexes.