Sample compression schemes for balls in graphs

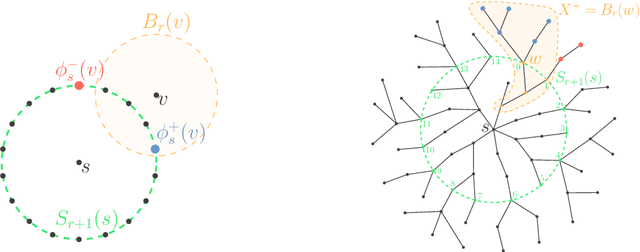
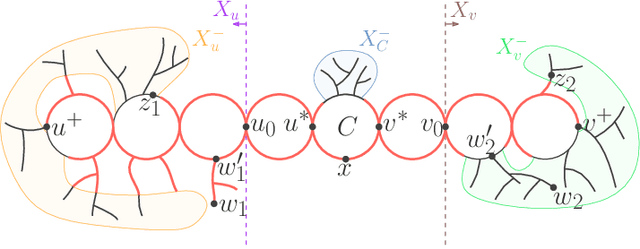
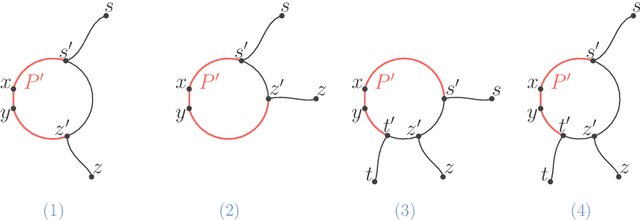
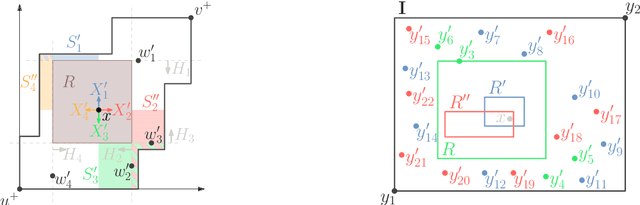
One of the open problems in machine learning is whether any set-family of VC-dimension $d$ admits a sample compression scheme of size~$O(d)$. In this paper, we study this problem for balls in graphs. For balls of arbitrary radius $r$, we design proper sample compression schemes of size $2$ for trees, of size $3$ for cycles, of size $4$ for interval graphs, of size $6$ for trees of cycles, and of size $22$ for cube-free median graphs. For balls of a given radius, we design proper labeled sample compression schemes of size $2$ for trees and of size $4$ for interval graphs. We also design approximate sample compression schemes of size 2 for balls of $\delta$-hyperbolic graphs.